 . Αν ο
. Αν ο  διαιρείται με το
διαιρείται με το  , να δειχθεί ότι διαιρείται και με το
, να δειχθεί ότι διαιρείται και με το  .
.Συντονιστής: Demetres

 είναι όλα να διαιρούνται από το
είναι όλα να διαιρούνται από το  και αφού το
και αφού το  είναι πρώτος το ζητούμενο αποδείχθηκε.
είναι πρώτος το ζητούμενο αποδείχθηκε. . Τότε το
. Τότε το  είναι αντιστρέψιμο
είναι αντιστρέψιμο  οπότε μπορούμε να βρούμε
οπότε μπορούμε να βρούμε  ώστε
ώστε  . Τώρα ο έλεγχος είναι πιο απλός και βλέπουμε ότι δεν υπάρχουν τέτοια
. Τώρα ο έλεγχος είναι πιο απλός και βλέπουμε ότι δεν υπάρχουν τέτοια  . Άρα
. Άρα  και ομοίως
και ομοίως 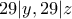 .
. με δεδομένο ότι ο
με δεδομένο ότι ο  είναι πρώτος αρκεί να ελέγξει για
είναι πρώτος αρκεί να ελέγξει για  και όπως γνωρίζουμε οι λύσεις θα είναι της μορφής
και όπως γνωρίζουμε οι λύσεις θα είναι της μορφής  και
και  το πλήθος συνεπώς
το πλήθος συνεπώς  το πλήθος λύσεις για την
το πλήθος λύσεις για την 
 αν
αν  τότε
τότε 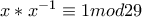 ,
,  μη μηδενικός ακέραιος.
μη μηδενικός ακέραιος. άρα
άρα (1)
(1) (2)
(2)  και τότε
και τότε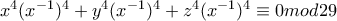
 και θέτω
και θέτω  ,
,  άρα αρκεί να λύσω την
άρα αρκεί να λύσω την που δεν έχει λύσεις άρα
που δεν έχει λύσεις άρα 

 τότε θα είναι και ο άλλος άρα το αποδείξαμε.
τότε θα είναι και ο άλλος άρα το αποδείξαμε. δεν είναι πολλαπλάσιος του
δεν είναι πολλαπλάσιος του  τότε πάλι με τον ίδιο τρόπο του αντιστρόφου καταλήγουμε σε άτοπο η αλλιώς
τότε πάλι με τον ίδιο τρόπο του αντιστρόφου καταλήγουμε σε άτοπο η αλλιώς
 (από Fermat) άρα
(από Fermat) άρα
 αδύνατον.
αδύνατον.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες