Σελίδα 1 από 1
SEEMOUS 2015/3
Δημοσιεύτηκε: Κυρ Μαρ 08, 2015 10:48 pm
από emouroukos
3) Για κάθε ακέραιο

, έστω
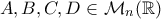
πίνακες για τους οποίους ισχύει

και

.
Να αποδειχθεί ότι:
α) 
και

,
β) 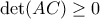
και

.
Re: SEEMOUS 2015/3
Δημοσιεύτηκε: Τρί Μαρ 10, 2015 6:00 pm
από Antonis_Z
Μια σκιαγράφηση λύσης(διαφορετικής απ'την επίσημη) για το-ομολογουμένως-δύσκολο 3β(το έλυσε πλήρως μόνο ένα άτομο στο διαγωνισμό).
Ας ονομάσουμε με τη σειρά τις 4 σχέσεις που έχουμε (1),(2),(3),(4).


Άρα

.
Επίσης,

και
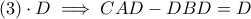
άρα

.
Τώρα

και

.
Με πρόσθεση των 2 τελευταίων

(λόγω των προηγούμενων σχέσεων).
Τέλος πάλι λόγω των προηγούμενων σχέσεων έχουμε

.
Για την απόδειξη της 2ης ανισότητας παρατηρήστε ότι είναι ισοδύναμη με την 1η...
Ουσιαστικά πρόκειται για την ιδέα της λύσης του Κωνσταντίνου Τσίνα απ'το διαγωνισμό.
Re: SEEMOUS 2015/3
Δημοσιεύτηκε: Τρί Ιούλ 25, 2017 5:08 pm
από Demetres
Βάζω μια απάντηση για το (α) που ήταν πιο απλό ώστε να κλείσει αυτό το θέμα:
Οι συνθήκες δίνουν

. Άρα είναι και
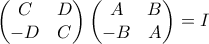
. Αυτό δίνει τις άλλες δύο συνθήκες.
 , έστω
, έστω 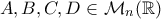 πίνακες για τους οποίους ισχύει
πίνακες για τους οποίους ισχύει  και
και  .
. και
και  ,
,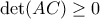 και
και  .
. , έστω
, έστω 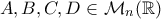 πίνακες για τους οποίους ισχύει
πίνακες για τους οποίους ισχύει  και
και  .
. και
και  ,
,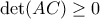 και
και  .
.

 .
.
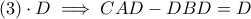
 .
. και
και  .
. (λόγω των προηγούμενων σχέσεων).
(λόγω των προηγούμενων σχέσεων). .
. . Άρα είναι και
. Άρα είναι και 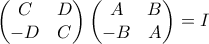 . Αυτό δίνει τις άλλες δύο συνθήκες.
. Αυτό δίνει τις άλλες δύο συνθήκες.