Δημήτρη, εγώ πήγα από το

στο

. (Δεν το δοκίμασες;)
Η πιθανότητα να κερδίσω για

είναι

η οποία είναι μεγαλύτερη του

. Έστω λοιπόν πως

και
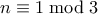
.
Επιλέγω τον

και μετά τον

. Αν είναι ο

κερδίζω, αν είναι ο

χάνω. Αν είναι ο

κερδίζω ενώ αν είναι μεγαλύτερος του

εφαρμόζω την στρατηγική επαγωγικά.
Η πιθανότητα νίκης είναι


Μια απόδειξη, η οποία είμαι σίγουρος πως προέκυψε από μια παρόμοια απόδειξη με την δική μου, είναι απίστευτα πιο όμορφη.
Επιλέγουμε διαδοχικά τους αριθμούς

μέχρι είτε να βρούμε τον ζητούμενο αριθμό είτε να μας πουν πως είναι μικρότερος από αυτόν που είπαμε.
Αν ο αριθμός είναι ο
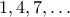
τότε κερδίζουμε.
Αν ο αριθμός είναι ο

τότε χάνουμε.
Αν ο αριθμός είναι ο

τότε κερδίζουμε. (Π.χ. αν είναι ο

σε άρτια κίνηση θα πούμε το

ενώ ήδη θα έχουμε πει τον

. Οπότε στην επόμενη περιττή κίνηση θα πούμε τον

.)
Άρα η πιθανότητα νίκης (με αυτήν την στρατηγική) είναι

Απλά

σε αυτόν που την βρήκε (είναι σε αρχείο των Kiran Kedlaya και Lenny Ng αλλά δεν ξέρω να είναι δική τους) και

που ήμουν τόσο κοντά αλλά δεν το πρόσεξα.

Μπορεί να δειχθεί ότι η βέλτιστη στρατηγική δίνει πιθανότητα νίκης

 επιλέγεται ομοιόμορφα στην τύχη από το διάστημα
επιλέγεται ομοιόμορφα στην τύχη από το διάστημα ![[1,2002] [1,2002]](/forum/ext/geomar/texintegr/latexrender/pictures/140c8c4380eae0ec02a6e82cc8a62945.png) .
.  μετά από περιττό αριθμό κινήσεων. Σε κάθε κίνηση μαντεύετε έναν αριθμό
μετά από περιττό αριθμό κινήσεων. Σε κάθε κίνηση μαντεύετε έναν αριθμό  από αυτό το διάστημα και πληροφορείστε αν
από αυτό το διάστημα και πληροφορείστε αν  ή
ή  ή
ή  . Κάθε φορά που μαντεύετε έναν αριθμό επιβάλλεται ο αριθμός αυτός να έχει θετική πιθανότητα να είναι ο επιλεγμένος αριθμός.
. Κάθε φορά που μαντεύετε έναν αριθμό επιβάλλεται ο αριθμός αυτός να έχει θετική πιθανότητα να είναι ο επιλεγμένος αριθμός.  μετά από περιττό αριθμό από μαντέματα να είναι μεγαλύτερη από
μετά από περιττό αριθμό από μαντέματα να είναι μεγαλύτερη από  .
.
 αριθμούς (έστω
αριθμούς (έστω  ) τότε η στρατηγική
) τότε η στρατηγική  (πρώτα το
(πρώτα το  και, σε περίπτωση αποτυχίας, το
και, σε περίπτωση αποτυχίας, το  ) μας εξασφαλίζει πιθανότητα επιτυχίας
) μας εξασφαλίζει πιθανότητα επιτυχίας  .
. αριθμούς. Αυτό αποδεικνύει και το αποτέλεσμα, αφού
αριθμούς. Αυτό αποδεικνύει και το αποτέλεσμα, αφού 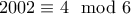 .
. . Αν ο αριθμός μας είναι πάνω από
. Αν ο αριθμός μας είναι πάνω από  (με πιθανότητα
(με πιθανότητα 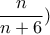 έχουμε πιθανότητα επιτυχίας
έχουμε πιθανότητα επιτυχίας  . Αν είναι μεταξύ
. Αν είναι μεταξύ  και
και  (με πιθανότητα
(με πιθανότητα 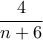 ) έχουμε πιθανότητα επιτυχίας
) έχουμε πιθανότητα επιτυχίας 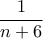 για το καθένα.)
για το καθένα.)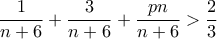 που ολοκληρώνει την απόδειξη.
που ολοκληρώνει την απόδειξη. . (Δεν το δοκίμασες;)
. (Δεν το δοκίμασες;) είναι
είναι  και
και 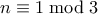 .
. 

 μέχρι είτε να βρούμε τον ζητούμενο αριθμό είτε να μας πουν πως είναι μικρότερος από αυτόν που είπαμε.
μέχρι είτε να βρούμε τον ζητούμενο αριθμό είτε να μας πουν πως είναι μικρότερος από αυτόν που είπαμε. 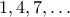 τότε κερδίζουμε.
τότε κερδίζουμε. τότε χάνουμε.
τότε χάνουμε. τότε κερδίζουμε. (Π.χ. αν είναι ο
τότε κερδίζουμε. (Π.χ. αν είναι ο  σε άρτια κίνηση θα πούμε το
σε άρτια κίνηση θα πούμε το  ενώ ήδη θα έχουμε πει τον
ενώ ήδη θα έχουμε πει τον  . Οπότε στην επόμενη περιττή κίνηση θα πούμε τον
. Οπότε στην επόμενη περιττή κίνηση θα πούμε τον 

 και παραμέλησα τελείως την τετριμμένη για
και παραμέλησα τελείως την τετριμμένη για