 πίνακες
πίνακες  .
.(α) Να δειχθεί ότι υπάρχει
 ώστε για κάθε
ώστε για κάθε  με
με  η εξίσωση
η εξίσωση
έχει μοναδική λύση
 στους πραγματικούς
στους πραγματικούς  πίνακες.
πίνακες.(β) Αν
 και ο
και ο  είναι διαγωνοποιήσιμος, να δειχθεί ότι
είναι διαγωνοποιήσιμος, να δειχθεί ότι 
Συντονιστής: Demetres
 πίνακες
πίνακες  .
. ώστε για κάθε
ώστε για κάθε  με
με  η εξίσωση
η εξίσωση
 στους πραγματικούς
στους πραγματικούς  πίνακες.
πίνακες. και ο
και ο  είναι διαγωνοποιήσιμος, να δειχθεί ότι
είναι διαγωνοποιήσιμος, να δειχθεί ότι 
 , όπου
, όπου  η (απόλυτα) μικρότερη μη μηδενική ιδιοτιμή του
η (απόλυτα) μικρότερη μη μηδενική ιδιοτιμή του  (ή
(ή  αν αυτή δεν υπάρχει) τότε ο
αν αυτή δεν υπάρχει) τότε ο  είναι αντιστρέψιμος και η εξίσωση έχει μοναδική λύση
είναι αντιστρέψιμος και η εξίσωση έχει μοναδική λύση  .
. , όπου
, όπου 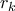 οι ιδιοτιμές του
οι ιδιοτιμές του  . Έτσι, το όριο ισούται με την αλγεβρική πολλαπλότητα της ιδιοτιμής
. Έτσι, το όριο ισούται με την αλγεβρική πολλαπλότητα της ιδιοτιμής  . Αυτή είναι ίση (λόγω διαγωνιοποιήσιμου) με τη μηδενικότητα του
. Αυτή είναι ίση (λόγω διαγωνιοποιήσιμου) με τη μηδενικότητα του  η οποία ισούται με το δεξί μέλος από το θεώρημα τάξης-μηδενικότητας.
η οποία ισούται με το δεξί μέλος από το θεώρημα τάξης-μηδενικότητας.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες