 ονομάζεται σπουδαίος αν
ονομάζεται σπουδαίος αν  για κάποιους θετικούς ακεραίους
για κάποιους θετικούς ακεραίους  . Να δειχθεί ότι για κάθε ακέραιο
. Να δειχθεί ότι για κάθε ακέραιο  υπάρχουν άπειροι θετικοί ακέραιοι
υπάρχουν άπειροι θετικοί ακέραιοι  ώστε το σύνολο
ώστε το σύνολο  να περιέχει ακριβώς
να περιέχει ακριβώς  σπουδαίους ακεραίους.
σπουδαίους ακεραίους.Συντονιστής: Demetres
 ονομάζεται σπουδαίος αν
ονομάζεται σπουδαίος αν  για κάποιους θετικούς ακεραίους
για κάποιους θετικούς ακεραίους  . Να δειχθεί ότι για κάθε ακέραιο
. Να δειχθεί ότι για κάθε ακέραιο  υπάρχουν άπειροι θετικοί ακέραιοι
υπάρχουν άπειροι θετικοί ακέραιοι  ώστε το σύνολο
ώστε το σύνολο  να περιέχει ακριβώς
να περιέχει ακριβώς  σπουδαίους ακεραίους.
σπουδαίους ακεραίους. το πλήθος των σπουδαίων αριθμών στο
το πλήθος των σπουδαίων αριθμών στο  . Θα αποδείξουμε το λήμμα ότι υπάρχουν άπειροι
. Θα αποδείξουμε το λήμμα ότι υπάρχουν άπειροι  με
με 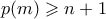 .
. αρκεί να βρούμε
αρκεί να βρούμε  τέτοιο ώστε ο
τέτοιο ώστε ο  να είναι τέλειο τετράγωνο. Έτσι, οι
να είναι τέλειο τετράγωνο. Έτσι, οι  είναι οι αριθμοί μας.
είναι οι αριθμοί μας.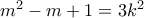 για κάποιο
για κάποιο  , που σημαίνει (από τη διακρίνουσα) ότι ο
, που σημαίνει (από τη διακρίνουσα) ότι ο  για κάποιο
για κάποιο  . Αρκεί λοιπόν
. Αρκεί λοιπόν  . Επειδή η διοφαντική
. Επειδή η διοφαντική  έχει άπειρες λύσεις (αρχίζοντας από
έχει άπειρες λύσεις (αρχίζοντας από  εφαρμόζουμε τον αναδρομικό τύπο
εφαρμόζουμε τον αναδρομικό τύπο  ) υπάρχουν άπειρα κατάλληλα
) υπάρχουν άπειρα κατάλληλα  .
. τα πράγματα είναι πιο απλά. Ισχύει
τα πράγματα είναι πιο απλά. Ισχύει  λόγω των
λόγω των 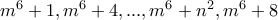 .
.  είναι το πολύ
είναι το πολύ  , οπότε η μέση απόσταση μεταξύ δύο σπουδαίων αριθμών αυξάνεται τουλάχιστον όπως
, οπότε η μέση απόσταση μεταξύ δύο σπουδαίων αριθμών αυξάνεται τουλάχιστον όπως  . Έτσι, υπάρχουν άπειρα
. Έτσι, υπάρχουν άπειρα  με
με  . Αφού, τέλος,
. Αφού, τέλος,  , ο
, ο  παίρνει άπειρες φορές όλες τις δυνατές τιμές μεταξύ του
παίρνει άπειρες φορές όλες τις δυνατές τιμές μεταξύ του  και του
και του  , οπότε υπάρχουν και άπειρα
, οπότε υπάρχουν και άπειρα  με
με  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες