SEEMOUS 2010
Συντονιστής: Demetres
- AlexandrosG
- Δημοσιεύσεις: 466
- Εγγραφή: Πέμ Οκτ 22, 2009 5:31 am
- Επικοινωνία:
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: SEEMOUS 2010
Βάζω μια λύση για το (4) διαφορετική από την επίσημη.
Αρκεί να δείξω ότι για κάθε πίνακα
πίνακα  με ρητά στοιχεία, υπάρχουν διακεκριμένοι αντιστρέψιμοι πίνακες
με ρητά στοιχεία, υπάρχουν διακεκριμένοι αντιστρέψιμοι πίνακες  με ακέραια στοιχεία ώστε
με ακέραια στοιχεία ώστε  .
.
Για h απόδειξη είναι με αιγυπτιακά κλάσματα ακριβώς όπως στην επίσημη λύση.
h απόδειξη είναι με αιγυπτιακά κλάσματα ακριβώς όπως στην επίσημη λύση.
Παρατηρώ ότι αν ο είναι αντιστρέψιμος πίνακας με ακέραια στοιχεία τότε και ο
είναι αντιστρέψιμος πίνακας με ακέραια στοιχεία τότε και ο  έχει ακέραια στοιχεία, και είναι αντιστρέψιμος με αντίστροφο τον
έχει ακέραια στοιχεία, και είναι αντιστρέψιμος με αντίστροφο τον  .
.
Για με
με 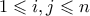 και
και  ορίζω τον
ορίζω τον  πίνακα
πίνακα  να έχει
να έχει  στην θέση
στην θέση  , άσους στις υπόλοιπες θέσεις της διαγωνίου,
, άσους στις υπόλοιπες θέσεις της διαγωνίου,  στην θέση
στην θέση  και μηδενικά στις υπόλοιπες θέσεις. Τότε ο
και μηδενικά στις υπόλοιπες θέσεις. Τότε ο  έχει
έχει  στην θέση
στην θέση  και μηδενικά σε όλες τις υπόλοιπες θέσεις που δεν είναι πάνω στην κύρια διαγώνιο. Χρησιμοποιώντας πίνακες της μορφής
και μηδενικά σε όλες τις υπόλοιπες θέσεις που δεν είναι πάνω στην κύρια διαγώνιο. Χρησιμοποιώντας πίνακες της μορφής  μπορώ να υποθέσω* ότι ο
μπορώ να υποθέσω* ότι ο  έχει μη μηδενικά στοιχεία μόνο πάνω στην κύρια διαγώνιο.
έχει μη μηδενικά στοιχεία μόνο πάνω στην κύρια διαγώνιο.
*Αρκεί να μην ξαναχρησιμοποιήσω πίνακες της μορφής . Όλοι όμως οι πίνακες που θα χρησιμοποιήσω από τώρα και στο εξής θα είναι διαγώνιοι.
. Όλοι όμως οι πίνακες που θα χρησιμοποιήσω από τώρα και στο εξής θα είναι διαγώνιοι.
Αρκεί να δείξω ότι για κάθε ρητό και κάθε
και κάθε  , ο πίνακας που έχει
, ο πίνακας που έχει  στην θέση
στην θέση  και 0 αλλού μπορεί να γραφεί σαν άθροισμα
και 0 αλλού μπορεί να γραφεί σαν άθροισμα  όπου οι πίνακες
όπου οι πίνακες  είναι διακεκριμένοι, διαγώνιοι, στην θέση
είναι διακεκριμένοι, διαγώνιοι, στην θέση  έχουν
έχουν  για κάποιο
για κάποιο  με
με  και στις υπόλοιπες διαγώνιες θέσεις έχουν είτε 1 είτε -1 είτε 1/2 είτε -1/2
και στις υπόλοιπες διαγώνιες θέσεις έχουν είτε 1 είτε -1 είτε 1/2 είτε -1/2
Γράφουμε όμως το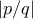 σαν αιγυπτιακό κλάσμα με τουλάχιστον δύο κλάσματα (με όλους τους παρονομαστές μεγαλύτερους ή ίσους του 3). Σε κάθε
σαν αιγυπτιακό κλάσμα με τουλάχιστον δύο κλάσματα (με όλους τους παρονομαστές μεγαλύτερους ή ίσους του 3). Σε κάθε  βάζουμε το αντίστοιχο κλάσμα στην θέση
βάζουμε το αντίστοιχο κλάσμα στην θέση  και διαλέγουμε πρόσημο το ίδιο με το πρόσημο του
και διαλέγουμε πρόσημο το ίδιο με το πρόσημο του  . Στις υπόλοιπες διαγώνιες θέσεις βάζουμε είτε 1 είτε -1 είτε 1/2 είτε -1/2 ώστε το άθροισμα να ισούται με 0. Μπορούμε πάντα να το κάνουμε. Π.χ. αν έχουμε άρτιο αριθμό πινάκων βάζουμε στις μισές θέσεις το 1 και στις άλλες μισές το -1. Αν έχουμε περιττό βάζουμε στην πρώτη το 1 στην δεύτερη και τρίτη -1/2 και στις υπόλοιπες
. Στις υπόλοιπες διαγώνιες θέσεις βάζουμε είτε 1 είτε -1 είτε 1/2 είτε -1/2 ώστε το άθροισμα να ισούται με 0. Μπορούμε πάντα να το κάνουμε. Π.χ. αν έχουμε άρτιο αριθμό πινάκων βάζουμε στις μισές θέσεις το 1 και στις άλλες μισές το -1. Αν έχουμε περιττό βάζουμε στην πρώτη το 1 στην δεύτερη και τρίτη -1/2 και στις υπόλοιπες  εναλλάξ.
εναλλάξ.
Ελπίζω να μην έχασα τίποτα.
Αρκεί να δείξω ότι για κάθε
 πίνακα
πίνακα  με ρητά στοιχεία, υπάρχουν διακεκριμένοι αντιστρέψιμοι πίνακες
με ρητά στοιχεία, υπάρχουν διακεκριμένοι αντιστρέψιμοι πίνακες  με ακέραια στοιχεία ώστε
με ακέραια στοιχεία ώστε  .
.Για
 h απόδειξη είναι με αιγυπτιακά κλάσματα ακριβώς όπως στην επίσημη λύση.
h απόδειξη είναι με αιγυπτιακά κλάσματα ακριβώς όπως στην επίσημη λύση.Παρατηρώ ότι αν ο
 είναι αντιστρέψιμος πίνακας με ακέραια στοιχεία τότε και ο
είναι αντιστρέψιμος πίνακας με ακέραια στοιχεία τότε και ο  έχει ακέραια στοιχεία, και είναι αντιστρέψιμος με αντίστροφο τον
έχει ακέραια στοιχεία, και είναι αντιστρέψιμος με αντίστροφο τον  .
.Για
 με
με 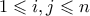 και
και  ορίζω τον
ορίζω τον  πίνακα
πίνακα  να έχει
να έχει  στην θέση
στην θέση  , άσους στις υπόλοιπες θέσεις της διαγωνίου,
, άσους στις υπόλοιπες θέσεις της διαγωνίου,  στην θέση
στην θέση  και μηδενικά στις υπόλοιπες θέσεις. Τότε ο
και μηδενικά στις υπόλοιπες θέσεις. Τότε ο  έχει
έχει  στην θέση
στην θέση  και μηδενικά σε όλες τις υπόλοιπες θέσεις που δεν είναι πάνω στην κύρια διαγώνιο. Χρησιμοποιώντας πίνακες της μορφής
και μηδενικά σε όλες τις υπόλοιπες θέσεις που δεν είναι πάνω στην κύρια διαγώνιο. Χρησιμοποιώντας πίνακες της μορφής  μπορώ να υποθέσω* ότι ο
μπορώ να υποθέσω* ότι ο  έχει μη μηδενικά στοιχεία μόνο πάνω στην κύρια διαγώνιο.
έχει μη μηδενικά στοιχεία μόνο πάνω στην κύρια διαγώνιο. *Αρκεί να μην ξαναχρησιμοποιήσω πίνακες της μορφής
 . Όλοι όμως οι πίνακες που θα χρησιμοποιήσω από τώρα και στο εξής θα είναι διαγώνιοι.
. Όλοι όμως οι πίνακες που θα χρησιμοποιήσω από τώρα και στο εξής θα είναι διαγώνιοι.Αρκεί να δείξω ότι για κάθε ρητό
 και κάθε
και κάθε  , ο πίνακας που έχει
, ο πίνακας που έχει  στην θέση
στην θέση  και 0 αλλού μπορεί να γραφεί σαν άθροισμα
και 0 αλλού μπορεί να γραφεί σαν άθροισμα  όπου οι πίνακες
όπου οι πίνακες  είναι διακεκριμένοι, διαγώνιοι, στην θέση
είναι διακεκριμένοι, διαγώνιοι, στην θέση  έχουν
έχουν  για κάποιο
για κάποιο  με
με  και στις υπόλοιπες διαγώνιες θέσεις έχουν είτε 1 είτε -1 είτε 1/2 είτε -1/2
και στις υπόλοιπες διαγώνιες θέσεις έχουν είτε 1 είτε -1 είτε 1/2 είτε -1/2Γράφουμε όμως το
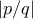 σαν αιγυπτιακό κλάσμα με τουλάχιστον δύο κλάσματα (με όλους τους παρονομαστές μεγαλύτερους ή ίσους του 3). Σε κάθε
σαν αιγυπτιακό κλάσμα με τουλάχιστον δύο κλάσματα (με όλους τους παρονομαστές μεγαλύτερους ή ίσους του 3). Σε κάθε  βάζουμε το αντίστοιχο κλάσμα στην θέση
βάζουμε το αντίστοιχο κλάσμα στην θέση  και διαλέγουμε πρόσημο το ίδιο με το πρόσημο του
και διαλέγουμε πρόσημο το ίδιο με το πρόσημο του  . Στις υπόλοιπες διαγώνιες θέσεις βάζουμε είτε 1 είτε -1 είτε 1/2 είτε -1/2 ώστε το άθροισμα να ισούται με 0. Μπορούμε πάντα να το κάνουμε. Π.χ. αν έχουμε άρτιο αριθμό πινάκων βάζουμε στις μισές θέσεις το 1 και στις άλλες μισές το -1. Αν έχουμε περιττό βάζουμε στην πρώτη το 1 στην δεύτερη και τρίτη -1/2 και στις υπόλοιπες
. Στις υπόλοιπες διαγώνιες θέσεις βάζουμε είτε 1 είτε -1 είτε 1/2 είτε -1/2 ώστε το άθροισμα να ισούται με 0. Μπορούμε πάντα να το κάνουμε. Π.χ. αν έχουμε άρτιο αριθμό πινάκων βάζουμε στις μισές θέσεις το 1 και στις άλλες μισές το -1. Αν έχουμε περιττό βάζουμε στην πρώτη το 1 στην δεύτερη και τρίτη -1/2 και στις υπόλοιπες  εναλλάξ.
εναλλάξ.Ελπίζω να μην έχασα τίποτα.
Re: SEEMOUS 2010
Demetres έγραψε:Βάζω μια λύση για το (4) διαφορετική από την επίσημη.
Αρκεί να δείξω ότι για κάθεπίνακα
με ρητά στοιχεία, υπάρχουν διακεκριμένοι αντιστρέψιμοι πίνακες
με ακέραια στοιχεία ώστε
.
Γιαh απόδειξη είναι με αιγυπτιακά κλάσματα ακριβώς όπως στην επίσημη λύση.
Παρατηρώ ότι αν οείναι αντιστρέψιμος πίνακας με ακέραια στοιχεία τότε και ο
έχει ακέραια στοιχεία, και είναι αντιστρέψιμος με αντίστροφο τον
.
Γιαμε
και
ορίζω τον
πίνακα
να έχει
στην θέση
, άσους στις υπόλοιπες θέσεις της διαγωνίου,
στην θέση
και μηδενικά στις υπόλοιπες θέσεις. Τότε ο
έχει
στην θέση
και μηδενικά σε όλες τις υπόλοιπες θέσεις που δεν είναι πάνω στην κύρια διαγώνιο. Χρησιμοποιώντας πίνακες της μορφής
μπορώ να υποθέσω* ότι ο
έχει μη μηδενικά στοιχεία μόνο πάνω στην κύρια διαγώνιο.
*Αρκεί να μην ξαναχρησιμοποιήσω πίνακες της μορφής. Όλοι όμως οι πίνακες που θα χρησιμοποιήσω από τώρα και στο εξής θα είναι διαγώνιοι.
Αρκεί να δείξω ότι για κάθε ρητόκαι κάθε
, ο πίνακας που έχει
στην θέση
και 0 αλλού μπορεί να γραφεί σαν άθροισμα
όπου οι πίνακες
είναι διακεκριμένοι, διαγώνιοι, στην θέση
έχουν
για κάποιο
με
και στις υπόλοιπες διαγώνιες θέσεις έχουν είτε 1 είτε -1 είτε 1/2 είτε -1/2
Γράφουμε όμως τοσαν αιγυπτιακό κλάσμα με τουλάχιστον δύο κλάσματα (με όλους τους παρονομαστές μεγαλύτερους ή ίσους του 3). Σε κάθε
βάζουμε το αντίστοιχο κλάσμα στην θέση
και διαλέγουμε πρόσημο το ίδιο με το πρόσημο του
. Στις υπόλοιπες διαγώνιες θέσεις βάζουμε είτε 1 είτε -1 είτε 1/2 είτε -1/2 ώστε το άθροισμα να ισούται με 0. Μπορούμε πάντα να το κάνουμε. Π.χ. αν έχουμε άρτιο αριθμό πινάκων βάζουμε στις μισές θέσεις το 1 και στις άλλες μισές το -1. Αν έχουμε περιττό βάζουμε στην πρώτη το 1 στην δεύτερη και τρίτη -1/2 και στις υπόλοιπες
εναλλάξ.
Ελπίζω να μην έχασα τίποτα.
Eίναι από όσο νομίζω η γενίκευση που μας έλεγε ότι απέδειξε ο (τριτος στην τελική κατάταξη) ισραηλινός στον seemous!!
Επίσης διαφορετική λύση απο τις επίσημες πιστεύω ειναι πολύ φυσιολογικό να δοθεί στο 3(α) παιρνωντας περιπτώσεις για τις ιδιοτιμές του A.
Re: SEEMOUS 2010
Θερμά συγχαρητήρια σε όλους τους συμμετέχοντες και ιδιαίτερα στους διακριθέντες!!!
Με ιδιαίτερη εκτίμηση και θαυμασμό,
Αχιλλέας
Με ιδιαίτερη εκτίμηση και θαυμασμό,
Αχιλλέας
- Κώστας Παππέλης
- Δημοσιεύσεις: 261
- Εγγραφή: Παρ Ιούλ 24, 2009 4:17 pm
- Τοποθεσία: Αθήνα
Re: SEEMOUS 2010
Χάριν πληρότητας να βάλω μια λύση στο ομολογουμένως δύσκολο 3α την οποία προσπάθησα να κάνω κατά τη διάρκεια του διαγωνισμού αλλά δε μου προχωρούσε και την ολοκλήρωσα σήμερα το πρωί ενώ διάβαζα ανθρωπολογία για τους πιθήκους.
Σπάμε τον στη πολική του διάσπαση με
στη πολική του διάσπαση με 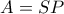 όπου ο
όπου ο  είναι θετικά ορισμένος και ο
είναι θετικά ορισμένος και ο  είναι ισομετρία (
είναι ισομετρία ( ). Τώρα ο
). Τώρα ο  έχει τετραγωνική ρίζα οπότε αρκεί να σπάσουμε τον
έχει τετραγωνική ρίζα οπότε αρκεί να σπάσουμε τον  σε άθροισμα δύο τετραγώνων.
σε άθροισμα δύο τετραγώνων.
Αυτό όμως επιτυγχάνεται ως εξής: ο γενικά σε n-διάστατο χώρο είναι όμοιος με έναν πίνακα σε blocks όπου κάθε block είναι είτε μια 2x2 rotation είτε ένας άσος είτε ένας μείον άσος.
γενικά σε n-διάστατο χώρο είναι όμοιος με έναν πίνακα σε blocks όπου κάθε block είναι είτε μια 2x2 rotation είτε ένας άσος είτε ένας μείον άσος.
Άρα στο πρόβλημά μας: αν είναι rotation τελειώσαμε (οι ιδιοτιμές δεν είναι πραγματικές), αν είναι ο identity ή ο μείον identity επίσης τελειώσαμε (είναι τέλεια τετράγωνα συν τον μηδενικό στο τετράγωνο) και τέλος αν έχει έναν άσο και έναν μείον άσο, προσθέτουμε στον μείον identity έναν πίνακα που έχει entry 2 και τα άλλα τρία του entries είναι 0.
Edit: Δυστυχώς η παραπάνω λύση δε δουλεύει (παρά μόνο για πίνακες με ορίζουσα +-1) γιατί χαλάει στο γινόμενο (το γινόμενο δύο τετραγώνων δεν είναι υποχρεωτικά τετράγωνο)
Ηλία ευχαριστώ για την επισήμανση.
Σπάμε τον
 στη πολική του διάσπαση με
στη πολική του διάσπαση με 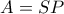 όπου ο
όπου ο  είναι θετικά ορισμένος και ο
είναι θετικά ορισμένος και ο  είναι ισομετρία (
είναι ισομετρία ( ). Τώρα ο
). Τώρα ο  έχει τετραγωνική ρίζα οπότε αρκεί να σπάσουμε τον
έχει τετραγωνική ρίζα οπότε αρκεί να σπάσουμε τον  σε άθροισμα δύο τετραγώνων.
σε άθροισμα δύο τετραγώνων.Αυτό όμως επιτυγχάνεται ως εξής: ο
 γενικά σε n-διάστατο χώρο είναι όμοιος με έναν πίνακα σε blocks όπου κάθε block είναι είτε μια 2x2 rotation είτε ένας άσος είτε ένας μείον άσος.
γενικά σε n-διάστατο χώρο είναι όμοιος με έναν πίνακα σε blocks όπου κάθε block είναι είτε μια 2x2 rotation είτε ένας άσος είτε ένας μείον άσος.Άρα στο πρόβλημά μας: αν είναι rotation τελειώσαμε (οι ιδιοτιμές δεν είναι πραγματικές), αν είναι ο identity ή ο μείον identity επίσης τελειώσαμε (είναι τέλεια τετράγωνα συν τον μηδενικό στο τετράγωνο) και τέλος αν έχει έναν άσο και έναν μείον άσο, προσθέτουμε στον μείον identity έναν πίνακα που έχει entry 2 και τα άλλα τρία του entries είναι 0.
Edit: Δυστυχώς η παραπάνω λύση δε δουλεύει (παρά μόνο για πίνακες με ορίζουσα +-1) γιατί χαλάει στο γινόμενο (το γινόμενο δύο τετραγώνων δεν είναι υποχρεωτικά τετράγωνο)
Ηλία ευχαριστώ για την επισήμανση.
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: SEEMOUS 2010
Έτυχε να γνωρίσω από κοντά τα περισσότερα από αυτά τα παιδιά που πήραν μέρος στο διαγωνισμό. Έχουν εξαιρετικό ήθος και πολύ ταλέντο.
Τα συγχαίρω με τη σειρά μου και εύχομαι καλή συνέχεια στις σπουδές τους, με διακρίσεις στην ανώτατη εκπαίδευση και στις επιστήμες
που επέλεξαν να υπηρετήσουν !
Μπάμπης
Τα συγχαίρω με τη σειρά μου και εύχομαι καλή συνέχεια στις σπουδές τους, με διακρίσεις στην ανώτατη εκπαίδευση και στις επιστήμες
που επέλεξαν να υπηρετήσουν !
Μπάμπης
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: SEEMOUS 2010
Δεν πειράζει -- η προσπάθεια είναι που μετράει, και στην συγκεκριμένη περίπτωση βοήθησε μάλλον και στις άλλες μελέτες σουΚώστας Παππέλης έγραψε:Χάριν πληρότητας να βάλω μια λύση στο ομολογουμένως δύσκολο 3α την οποία προσπάθησα να κάνω κατά τη διάρκεια του διαγωνισμού αλλά δε μου προχωρούσε και την ολοκλήρωσα σήμερα το πρωί ενώ διάβαζα ανθρωπολογία για τους πιθήκους.
Σπάμε τονστη πολική του διάσπαση με
όπου ο
είναι θετικά ορισμένος και ο
είναι ισομετρία (
). Τώρα ο
έχει τετραγωνική ρίζα οπότε αρκεί να σπάσουμε τον
σε άθροισμα δύο τετραγώνων.
Αυτό όμως επιτυγχάνεται ως εξής: ογενικά σε n-διάστατο χώρο είναι όμοιος με έναν πίνακα σε blocks όπου κάθε block είναι είτε μια 2x2 rotation είτε ένας άσος είτε ένας μείον άσος.
Άρα στο πρόβλημά μας: αν είναι rotation τελειώσαμε (οι ιδιοτιμές δεν είναι πραγματικές), αν είναι ο identity ή ο μείον identity επίσης τελειώσαμε (είναι τέλεια τετράγωνα συν τον μηδενικό στο τετράγωνο) και τέλος αν έχει έναν άσο και έναν μείον άσο, προσθέτουμε στον μείον identity έναν πίνακα που έχει entry 2 και τα άλλα τρία του entries είναι 0.
Edit: Δυστυχώς η παραπάνω λύση δε δουλεύει (παρά μόνο για πίνακες με ορίζουσα +-1) γιατί χαλάει στο γινόμενο (το γινόμενο δύο τετραγώνων δεν είναι υποχρεωτικά τετράγωνο)
Συγχαρητήρια σε όλους σας,
Γιώργος Μπαλόγλου
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- bilstef
- Δημοσιεύσεις: 1391
- Εγγραφή: Σάβ Δεκ 20, 2008 11:45 pm
- Τοποθεσία: Χαλάνδρι - Κομοτηνή
- Επικοινωνία:
ΔΙΆΚΡΙΣΗ ΣΤΟΝ SEEMOUS 2010 Πάλι
Από email που πήρα από gpapado@civil.duth.gr; Γεωργία Φακά-Παπαδοπούλου
Δεύτερο Χάλκινο Μετάλλιο στην Πολυτεχνική Σχολή του Δ.Π.Θ.
σε Μαθηματική Ολυμπιάδα για φοιτητές Α.Ε.Ι.
Στη Φιλιππούπολη της Βουλγαρίας, διεξήχθη η 4η Μαθηματική Ολυμπιάδα
για φοιτητές Ανωτάτων Εκπαιδευτικών Ιδρυμάτων της Νοτιανατολικής
Ευρώπης (SEEMOUS 2010), South Eastern European Mathematical for
University students with International Participation από 8-12 Μαρτίου.
Η τριμελής αποστολή φοιτητών της Πολυτεχνικής Σχολής, με τον Υπεύθυνο
Καθηγητή κ. Β. Παπαδόπουλο, διαγωνίσθηκε με φοιτητές Μαθηματικών
Τμημάτων, Τμημάτων Πληροφορικής και Τμημάτων Πολυτεχνείων, της Ελλάδας
και χωρών με μεγάλη παράδοση στα μαθηματικά.
Στην εν λόγω διοργάνωση, ο φοιτητής του Τμήματος Πολιτικών Μηχανικών,
Adjenughhure Kingsley από τη Νιγηρία, ανέβασε την αποστολή του
Δημοκριτείου Πανεπιστημίου Θράκης, στο βάθρο των νικητών, κατακτώντας
Xάλκινο Mετάλλιο.
Υπενθυμίζουμε την απόκτηση Χάλκινου Μεταλλίου, από τον φοιτητή του
Τμήματος Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών, Ιωάννη
Σεϊτανίδη, στην 3η Μαθηματική Ολυμπιάδα στην Κύπρο.
Δεύτερο Χάλκινο Μετάλλιο στην Πολυτεχνική Σχολή του Δ.Π.Θ.
σε Μαθηματική Ολυμπιάδα για φοιτητές Α.Ε.Ι.
Στη Φιλιππούπολη της Βουλγαρίας, διεξήχθη η 4η Μαθηματική Ολυμπιάδα
για φοιτητές Ανωτάτων Εκπαιδευτικών Ιδρυμάτων της Νοτιανατολικής
Ευρώπης (SEEMOUS 2010), South Eastern European Mathematical for
University students with International Participation από 8-12 Μαρτίου.
Η τριμελής αποστολή φοιτητών της Πολυτεχνικής Σχολής, με τον Υπεύθυνο
Καθηγητή κ. Β. Παπαδόπουλο, διαγωνίσθηκε με φοιτητές Μαθηματικών
Τμημάτων, Τμημάτων Πληροφορικής και Τμημάτων Πολυτεχνείων, της Ελλάδας
και χωρών με μεγάλη παράδοση στα μαθηματικά.
Στην εν λόγω διοργάνωση, ο φοιτητής του Τμήματος Πολιτικών Μηχανικών,
Adjenughhure Kingsley από τη Νιγηρία, ανέβασε την αποστολή του
Δημοκριτείου Πανεπιστημίου Θράκης, στο βάθρο των νικητών, κατακτώντας
Xάλκινο Mετάλλιο.
Υπενθυμίζουμε την απόκτηση Χάλκινου Μεταλλίου, από τον φοιτητή του
Τμήματος Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών, Ιωάννη
Σεϊτανίδη, στην 3η Μαθηματική Ολυμπιάδα στην Κύπρο.
Η ζωή είναι Ωραία,ας την χαρούμε.Εν οίδα ότι ουδέν οίδα!Γηράσκω αεί διδασκόμενος!
Η γη δεν μας ανήκει της ανήκουμε !
Βασίλης Στεφανίδης
Η γη δεν μας ανήκει της ανήκουμε !
Βασίλης Στεφανίδης
Re: SEEMOUS 2010
Καλησπέρα σας!
Στο άρθρο Olimpiada de matematica a studentilor din sud-estul Europei, SEEMOUS 2010, σελ. 38-48 , υπάρχουν εναλλλακτικές λύσεις και ενδιαφέρουσες πληροφορίες.
Φιλικά,
Αχιλλέας
Στο άρθρο Olimpiada de matematica a studentilor din sud-estul Europei, SEEMOUS 2010, σελ. 38-48 , υπάρχουν εναλλλακτικές λύσεις και ενδιαφέρουσες πληροφορίες.
Φιλικά,
Αχιλλέας
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
