Σελίδα 1 από 1
Putnam 2017/A3
Δημοσιεύτηκε: Δευ Δεκ 04, 2017 10:31 am
από Demetres
Έστω πραγματικοί αριθμοί

, με
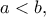
και διακεκριμένες συνεχείς συναρτήσεις

από το
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
στο

ώστε

Για θετικό ακέραιο

ορίζουμε

Να δειχθεί ότι η ακολουθία

είναι αύξουσα και

Re: Putnam 2017/A3
Δημοσιεύτηκε: Τρί Δεκ 05, 2017 6:38 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Demetres έγραψε: ↑Δευ Δεκ 04, 2017 10:31 am
Έστω πραγματικοί αριθμοί

, με
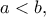
και διακεκριμένες συνεχείς συναρτήσεις

από το
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
στο

ώστε

Για θετικό ακέραιο

ορίζουμε

Να δειχθεί ότι η ακολουθία

είναι αύξουσα και

Θα δώσω μια λύση για την γενικότερη περίπτωση.
Δηλαδή υποθέτουμε ότι οι

είναι μετρήσιμες ,παίρνουν τιμές στο

,δεν είναι ίσες σχεδόν παντού και
είναι φραγμένες άνω για να μην μπορούν τα ολοκληρώματα να απειρίζονται.
(εννοείται ότι τα ολοκληρώματα είναι με την έννοια του Lebesgue)
Επίσης όλα τα σύνολα που ορίζονται παρακάτω είναι μετρήσιμα.
Τα σύνολα

έχουν μη μηδενικό μέτρο αφού οι συναρτήσεις δεν είναι ίσες σχεδόν παντού και

(στα ολοκληρώματα παραλείπω τα

)
i)Είναι

Αλλά

γιατί στο

είναι

.
Η απόδειξη του i) ολοκληρώθηκε
ii)Γράφουμε

Είναι

Επειδή το

εχει θετικό μέτρο υπάρχει

ώστε το

να έχει θετικό μέτρο.
Αλλά


άρα υπάρχει

ώστε το σύνολο

να έχει θετικό μέτρο.
Τελικά είναι

Δεν έβαλα άκρα ολοκλήρωσης γιατί με κάποιες προυποθέσεις ισχύει και για μη κλειστά διαστήματα.
Re: Putnam 2017/A3
Δημοσιεύτηκε: Τετ Δεκ 06, 2017 6:34 pm
από panos99
Το ίδιο πρόβλημα τέθηκε στην RNMO 2003 με μοναδική διαφορά ότι τα ολοκληρώματα ήταν από 0 έως 1.
Re: Putnam 2017/A3
Δημοσιεύτηκε: Πέμ Δεκ 07, 2017 11:03 am
από Demetres
Παναγιώτη, ευχαριστούμε για την πληροφόρηση. Το RNMO τι συμβολίζει; Romanian National Mathematical Olympiad, ή μήπως κάτι άλλο;
Re: Putnam 2017/A3
Δημοσιεύτηκε: Παρ Δεκ 08, 2017 9:19 pm
από Mihalis_Lambrou
Demetres έγραψε: ↑Δευ Δεκ 04, 2017 10:31 am
Έστω πραγματικοί αριθμοί

, με
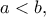
και διακεκριμένες συνεχείς συναρτήσεις

από το
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
στο

ώστε

Για θετικό ακέραιο

ορίζουμε

Να δειχθεί ότι η ακολουθία

είναι αύξουσα και

Αλλιώς: Θεωρούμε την αληθή ανισότητα

, με την παρατήρηση ότι σε κάποιο σημείο η ανισότητα πρέπει να είναι γνήσια γιατί οι

δεν ταυτίζονται. Πολλαπλασιάζουμε επί

και ολοκληρώνουμε. Δίνει

(γνήσια ανισότητα λόγω της παρατήρησης και το γεγονός ότι έχουμε να κάνουμε με συνεχείς συναρτήσεις).
Άρα

και επαγωγικά

. Ειδικά,

, που απαντά στο πρώτο ερώτημα.
Πρόσθεση κατά μέλη των

δίνει

, που απαντά στο δεύτερο ερώτημα.
Re: Putnam 2017/A3
Δημοσιεύτηκε: Σάβ Δεκ 16, 2017 11:10 am
από panos99
Κι εγώ έτσι νομίζω αλλά δεν είμαι σίγουρος. Παραθέτω την πηγή μου (Problem 64)
https://lupucezar.files.wordpress.com/2 ... tions_.pdf
 , με
, με 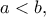 και διακεκριμένες συνεχείς συναρτήσεις
και διακεκριμένες συνεχείς συναρτήσεις  από το
από το ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) στο
στο  ώστε
ώστε 
 ορίζουμε
ορίζουμε 
 είναι αύξουσα και
είναι αύξουσα και 
 , με
, με 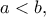 και διακεκριμένες συνεχείς συναρτήσεις
και διακεκριμένες συνεχείς συναρτήσεις  από το
από το ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) στο
στο  ώστε
ώστε 
 ορίζουμε
ορίζουμε 
 είναι αύξουσα και
είναι αύξουσα και 


 )
)

 είναι
είναι  .
.

 εχει θετικό μέτρο υπάρχει
εχει θετικό μέτρο υπάρχει 
 να έχει θετικό μέτρο.
να έχει θετικό μέτρο.




 , με την παρατήρηση ότι σε κάποιο σημείο η ανισότητα πρέπει να είναι γνήσια γιατί οι
, με την παρατήρηση ότι σε κάποιο σημείο η ανισότητα πρέπει να είναι γνήσια γιατί οι  και ολοκληρώνουμε. Δίνει
και ολοκληρώνουμε. Δίνει  (γνήσια ανισότητα λόγω της παρατήρησης και το γεγονός ότι έχουμε να κάνουμε με συνεχείς συναρτήσεις).
(γνήσια ανισότητα λόγω της παρατήρησης και το γεγονός ότι έχουμε να κάνουμε με συνεχείς συναρτήσεις). και επαγωγικά
και επαγωγικά  . Ειδικά,
. Ειδικά,  , που απαντά στο πρώτο ερώτημα.
, που απαντά στο πρώτο ερώτημα.  δίνει
δίνει  , που απαντά στο δεύτερο ερώτημα.
, που απαντά στο δεύτερο ερώτημα.