 της μορφής
της μορφής  όπου το κλάσμα είναι ανάγωγο , ορίζουμε
όπου το κλάσμα είναι ανάγωγο , ορίζουμε  . Να υπολογιστεί το άθροισμα:
. Να υπολογιστεί το άθροισμα:
Συντονιστής: Demetres
 της μορφής
της μορφής  όπου το κλάσμα είναι ανάγωγο , ορίζουμε
όπου το κλάσμα είναι ανάγωγο , ορίζουμε  . Να υπολογιστεί το άθροισμα:
. Να υπολογιστεί το άθροισμα:


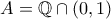 . Έστω
. Έστω  , οπότε
, οπότε  για κάποιους σχετικά πρώτους θετικούς ακεραίους
για κάποιους σχετικά πρώτους θετικούς ακεραίους  με
με  . Θεωρούμε επίσης τα σύνολα:
. Θεωρούμε επίσης τα σύνολα:
 είναι ισοπληθικά με τα
είναι ισοπληθικά με τα 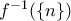 , για κάθε
, για κάθε 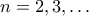 - εδώ παίρνουμε την
- εδώ παίρνουμε την  περιορισμένη στο
περιορισμένη στο  , αλλιώς το
, αλλιώς το  έχει τη διπλάσια πληθικότητα, γενικά.. Πράγματι, αν πάρουμε ένα
έχει τη διπλάσια πληθικότητα, γενικά.. Πράγματι, αν πάρουμε ένα  με
με  , τότε έπεται ότι
, τότε έπεται ότι  , όπου
, όπου  είναι δύο σχετικά πρώτοι θετικοί ακέραιοι με
είναι δύο σχετικά πρώτοι θετικοί ακέραιοι με  και, αντίστροφα, για κάθε ζεύγος
και, αντίστροφα, για κάθε ζεύγος  της παραπάνω μορφής έχουμε ένα κλάσμα
της παραπάνω μορφής έχουμε ένα κλάσμα  με
με  .
. το πλήθος των διακεκριμένων πρώτων διαιρετών του
το πλήθος των διακεκριμένων πρώτων διαιρετών του  , οπότε:
, οπότε: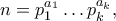
 για
για  . Για να επιλέξουμε ένα ζεύγος
. Για να επιλέξουμε ένα ζεύγος  σχετικά πρώτων διαιρετών του
σχετικά πρώτων διαιρετών του  με
με  αρκεί να επιλέξουμε ένα υποσύνολο
αρκεί να επιλέξουμε ένα υποσύνολο  και να θέσουμε:
και να θέσουμε:
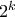 τέτοια ζευγάρια. Για να βρούμε το πλήθος του
τέτοια ζευγάρια. Για να βρούμε το πλήθος του  , ας παρατηρήσουμε ότι, αφού
, ας παρατηρήσουμε ότι, αφού  , το
, το  περιέχει ακριβώς τα μισά από τα πιθανά ζεύγη σχετικά πρώτων διαιρετών του
περιέχει ακριβώς τα μισά από τα πιθανά ζεύγη σχετικά πρώτων διαιρετών του  με
με  , άρα
, άρα  . Τώρα παρατηρούμε ότι το ζητούμενο όριο παίρνει τη μορφή:
. Τώρα παρατηρούμε ότι το ζητούμενο όριο παίρνει τη μορφή:
 καθώς
καθώς  για «σχεδόν όλους» τους φυσικούς αριθμούς, οπότε η προς άθροιση ακολουθία συγκρίνεται με την:
για «σχεδόν όλους» τους φυσικούς αριθμούς, οπότε η προς άθροιση ακολουθία συγκρίνεται με την:
 ισχύουν ακριβώς τα ίδια - αφού κάθε κλάσμα
ισχύουν ακριβώς τα ίδια - αφού κάθε κλάσμα 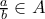 αντιστοιχίζεται με «1-1» και επί τρόπο στο ξαδερφάκι του
αντιστοιχίζεται με «1-1» και επί τρόπο στο ξαδερφάκι του  , οπότε, τελικά:
, οπότε, τελικά:

 . Τόλη, επιβεβαίωσε πριν κάτσω να γράψω τη λύση.
. Τόλη, επιβεβαίωσε πριν κάτσω να γράψω τη λύση.Γεια σου Δημήτρη ,
 .
.
 πρώτων αριθμών θα γράφω
πρώτων αριθμών θα γράφω  και
και 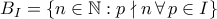 . Τότε έχουμε:
. Τότε έχουμε:
 .
. 

 το σύνολο των πρώτων αριθμών τότε
το σύνολο των πρώτων αριθμών τότε
 συγκλίνει για
συγκλίνει για  .
.
 είναι:
είναι: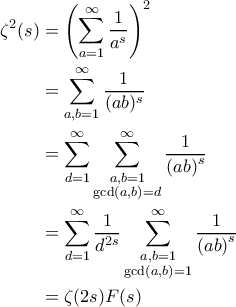
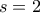 .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες