Πρόβλημα 1:
Θεωρούμε μιγαδικούς τετραγωνικούς πίνακες
 διάστασης
διάστασης  για τους οποίους
για τους οποίους  . Να αποδειχθεί ότι:
. Να αποδειχθεί ότι:(α)

(β)
 .
.Πρόβλημα 2:
Θεωρούμε πραγματικούς αριθμούς
 με
με  και
και  . Μια συνάρτηση
. Μια συνάρτηση  ονομάζεται Palic αν είναι συνεχής και για κάθε
ονομάζεται Palic αν είναι συνεχής και για κάθε  ισχύει η σχέση
ισχύει η σχέση 
Να αποδειχθεί ότι κάθε συνάρτηση Palic είναι άπειρες φορές παραγωγίσιμη και να βρεθούν όλες οι συναρτήσεις Palic.
Πρόβλημα 3:
Θεωρούμε μη μηδενικό μιγαδικό αριθμό
 και πίνακα
και πίνακα  για τους οποίους ισχύει η σχέση
για τους οποίους ισχύει η σχέση 
Να αποδειχθεί ότι
 ,
,  και ότι ο
και ότι ο  είναι κανονικός.
είναι κανονικός.Πρόβλημα 4:
Έστω
 η οικογένεια των μη κενών και πεπερασμένων υποσυνόλων του
η οικογένεια των μη κενών και πεπερασμένων υποσυνόλων του  . Να εξεταστεί για ποιους θετικούς πραγματικούς αριθμούς
. Να εξεταστεί για ποιους θετικούς πραγματικούς αριθμούς  η σειρά
η σειρά
συγκλίνει.

 . Είναι προφανές ότι αποκλίνει για
. Είναι προφανές ότι αποκλίνει για  αφού είναι άθροισμα θετικών όρων ανάμεσα στους οποίους είναι και οι
αφού είναι άθροισμα θετικών όρων ανάμεσα στους οποίους είναι και οι  . Μπορούμε λοιπόν να υποθέσουμε ότι
. Μπορούμε λοιπόν να υποθέσουμε ότι  . Τότε για κάθε πεπερασμένο
. Τότε για κάθε πεπερασμένο 
 υποσύνολα
υποσύνολα  αφού μπορούμε να αποφασίσουμε ανεξάρτητα για κάθε ένα από τα
αφού μπορούμε να αποφασίσουμε ανεξάρτητα για κάθε ένα από τα  αν ανήκουν στο
αν ανήκουν στο 
 υποσύνολα
υποσύνολα  με
με 



 . (Από κριτήριο πηλίκου για
. (Από κριτήριο πηλίκου για  και από αρμονική σειρά για
και από αρμονική σειρά για 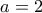 .)
.) .
. για τα rank .Είναι:
για τα rank .Είναι:
 , αφού
, αφού 

 που ήταν το ζητούμενο.
που ήταν το ζητούμενο.




 το ελάχιστο πολυώνυμο του
το ελάχιστο πολυώνυμο του  τότε προφανώς
τότε προφανώς ,άρα ο
,άρα ο  .
. οπότε ο
οπότε ο  ,
, και η γνωστή ισότητα
και η γνωστή ισότητα  μας δίνει το ζητούμενο.
μας δίνει το ζητούμενο. για τους οποίους ισχύει η σχέση
για τους οποίους ισχύει η σχέση 
 , τότε πολλαπλασιάζοντας την ζητούμενη με
, τότε πολλαπλασιάζοντας την ζητούμενη με  από δεξιά και
από δεξιά και  απο αριστερά, προκύπτει
απο αριστερά, προκύπτει 
 .
. .
.
 ,
,  , πρέπει να έχουμε ισότητα σε όλα τα
, πρέπει να έχουμε ισότητα σε όλα τα  πιο πάνω.
πιο πάνω. (μη-κενό αφού
(μη-κενό αφού  . Η ζητούμενη, αφού πολλαπλασιάσουμε από αριστερά με
. Η ζητούμενη, αφού πολλαπλασιάσουμε από αριστερά με  και από δεξιά με
και από δεξιά με  , γράφεται ως
, γράφεται ως
 κανονικός, που σημαίνει unitarily διαγωνοποιήσιμος.
κανονικός, που σημαίνει unitarily διαγωνοποιήσιμος.  ιδιοτιμή του
ιδιοτιμή του  δίνει
δίνει  , άρα
, άρα 
 αντιστρέψιμος) τη σχέση
αντιστρέψιμος) τη σχέση
 ,
,  .
. , και
, και  με κάποιες πολλαπλότητες.
με κάποιες πολλαπλότητες. , άρα
, άρα 
 (το ζητούμενο).
(το ζητούμενο).