Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
Συντονιστής: spyros
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
15ο ΣΗΜΕΙΩΜΑ
Προλεγόμενα Παρακάτω δημοσιεύουμε αποσπάσματα από μια διάλεξη (μεταξύ τριών διαλέξεων) του ομότιμου καθηγητή του πανεπιστημίου της Αθήνας, του Σπύρου Ζερβού (στο εξής Σ.Ζ.), που πραγματοποιήθηκαν το 1991. Δημοσιεύουμε αποσπάσματα της δεύτερης διάλεξης, η οποία είχε για τίτλο «Στοιχειώδης εισαγωγή σε έννοιες και προβλήματα της Λογικής και των Μαθηματικών». Ο Σ.Ζ. δημοσίευσε τις διαλέξεις με τη μορφή "ερώτησης-απάντησης". Το δημοσίευμα θα δοθεί σε δύο συνέχειες. Ακολουθεί το πρώτο κείμενο
"Μαθηματική περιγραφή φυσικών καταστάσεων"
«ΕΡΩΤΗΜΑ: Ποιος είναι ο συγκεκριμένος τρόπος, με τον οποίο περιγράφουμε μαθηματικά φυσικές καταστάσεις;
ΑΠΑΝΤΗΣΗ: Ένα κατανοητό απ’ όλους παράδειγμα είναι η μετάβαση από την εικόνα του χώρου που μας δίνουν οι αισθήσεις (όραση και αφή) στην Ευκλείδεια Γεωμετρία, σαν ιδεατή μαθηματική περιγραφή του. Θεμελιώδες επίτευγμα των αρχαίων Ελλήνων υπήρξε, εδώ, η αφαίρεση των διαστάσεων˙ δηλαδή, πως, από τα τρισδιάστατα υλικά αντικείμενα, φτάσανε στα τρισδιάστατα νοερά, ύστερα στα δισδιάστατα και τα μονοδιάστατα νοερά, και, το δυσκολότερο, στο χωρίς διαστάσεις σημείο. Λέει, σχετικά, ο Ήρων ο Αλεξανδρεύς, ότι, στην αρχή, ο άνθρωπος διαχώρισε το γεωμετρικό από το φυσικό στερεό˙ και ύστερα, «δι’ αφαιρέσεως κατήντησεν επί το σημείον». Μέσα σ’ αυτές τις δυο γραμμές βρίσκεται η μια από τις δύο θεμελιωδέστερες προϋποθέσεις για τη δημιουργία της επιστήμης˙ η άλλη, ήταν η έννοια του αφηρημένου αριθμού˙ δηλ. πως από τα "πέντε μήλα" πήγαμε στον αριθμό "πέντε"˙ μετάβαση, που ασφαλώς δεν έγινε δια μιας στο σύνολο των "φυσικών αριθμών"…»
«ΕΡΩΤΗΜΑ: Ποια Μαθηματικά εισάγουμε στην περιγραφή της Φύσης;
ΑΠΑΝΤΗΣΗ: α) από εκείνα που ξέρουμε κάθε φορά. Έτσι, στην Αναγέννηση, οι σοφοί της Ευρώπης αρχίσανε με την κληρονομημένη απ’ τους Έλληνες χρησιμοποίηση της Ευκλείδειας Γεωμετρίας στην Αστρονομία. Πολύ αργότερα, ο κορυφαίος Γάλλος μαθηματικός Ερρίκος Πουανκαρέ (1854-1912) θα χρησιμοποιήσει, σε πρωτοφανή έκταση και βάθος, στην Ουράνια Μηχανική, τη θεωρία των Αναλυτικών Μιγαδικών Συναρτήσεων, στην οποία είχε θαυματουργήσει, β) Ακόμα, εκείνα, στη διαμόρφωση των οποίων, μας έδωσαν τις αφορμές, οι ίδιες οι διαπιστώσεις και οι ανάγκες από τις φυσικές καταστάσεις. Περιληπτικά: έτσι, ζευγαρωμένα, ο Νεύτων ανέπτυξε τη Μηχανική και τον Απειροστικό Λογισμό. Γι’ αυτό και, παρ’ ότι είχε την ουσιαστική ακριβολογία του μεγάλου, ο Απειροστικός του ήταν κυριαρχημένος από την κινητική θεώρηση σε βαθμό, που (με την ορμή που εμπνέουν, και τη συγκομιδή ορθών ή όχι αποτελεσμάτων, που χαρίζουν, οι διαισθητικοί τρόποι) ανέστειλε για δύο αιώνες την ανάσταση της απόλυτα αυστηρής "στατικής" θεωρήσεως εννοιών του Απειροστικού από κορυφαίους αρχαίους Έλληνες μαθηματικούς (Εύδοξος, Αρχιμήδης, …….)»
με εκτίμηση
Γιάννης Κερασαρίδης
Προλεγόμενα Παρακάτω δημοσιεύουμε αποσπάσματα από μια διάλεξη (μεταξύ τριών διαλέξεων) του ομότιμου καθηγητή του πανεπιστημίου της Αθήνας, του Σπύρου Ζερβού (στο εξής Σ.Ζ.), που πραγματοποιήθηκαν το 1991. Δημοσιεύουμε αποσπάσματα της δεύτερης διάλεξης, η οποία είχε για τίτλο «Στοιχειώδης εισαγωγή σε έννοιες και προβλήματα της Λογικής και των Μαθηματικών». Ο Σ.Ζ. δημοσίευσε τις διαλέξεις με τη μορφή "ερώτησης-απάντησης". Το δημοσίευμα θα δοθεί σε δύο συνέχειες. Ακολουθεί το πρώτο κείμενο
"Μαθηματική περιγραφή φυσικών καταστάσεων"
«ΕΡΩΤΗΜΑ: Ποιος είναι ο συγκεκριμένος τρόπος, με τον οποίο περιγράφουμε μαθηματικά φυσικές καταστάσεις;
ΑΠΑΝΤΗΣΗ: Ένα κατανοητό απ’ όλους παράδειγμα είναι η μετάβαση από την εικόνα του χώρου που μας δίνουν οι αισθήσεις (όραση και αφή) στην Ευκλείδεια Γεωμετρία, σαν ιδεατή μαθηματική περιγραφή του. Θεμελιώδες επίτευγμα των αρχαίων Ελλήνων υπήρξε, εδώ, η αφαίρεση των διαστάσεων˙ δηλαδή, πως, από τα τρισδιάστατα υλικά αντικείμενα, φτάσανε στα τρισδιάστατα νοερά, ύστερα στα δισδιάστατα και τα μονοδιάστατα νοερά, και, το δυσκολότερο, στο χωρίς διαστάσεις σημείο. Λέει, σχετικά, ο Ήρων ο Αλεξανδρεύς, ότι, στην αρχή, ο άνθρωπος διαχώρισε το γεωμετρικό από το φυσικό στερεό˙ και ύστερα, «δι’ αφαιρέσεως κατήντησεν επί το σημείον». Μέσα σ’ αυτές τις δυο γραμμές βρίσκεται η μια από τις δύο θεμελιωδέστερες προϋποθέσεις για τη δημιουργία της επιστήμης˙ η άλλη, ήταν η έννοια του αφηρημένου αριθμού˙ δηλ. πως από τα "πέντε μήλα" πήγαμε στον αριθμό "πέντε"˙ μετάβαση, που ασφαλώς δεν έγινε δια μιας στο σύνολο των "φυσικών αριθμών"…»
«ΕΡΩΤΗΜΑ: Ποια Μαθηματικά εισάγουμε στην περιγραφή της Φύσης;
ΑΠΑΝΤΗΣΗ: α) από εκείνα που ξέρουμε κάθε φορά. Έτσι, στην Αναγέννηση, οι σοφοί της Ευρώπης αρχίσανε με την κληρονομημένη απ’ τους Έλληνες χρησιμοποίηση της Ευκλείδειας Γεωμετρίας στην Αστρονομία. Πολύ αργότερα, ο κορυφαίος Γάλλος μαθηματικός Ερρίκος Πουανκαρέ (1854-1912) θα χρησιμοποιήσει, σε πρωτοφανή έκταση και βάθος, στην Ουράνια Μηχανική, τη θεωρία των Αναλυτικών Μιγαδικών Συναρτήσεων, στην οποία είχε θαυματουργήσει, β) Ακόμα, εκείνα, στη διαμόρφωση των οποίων, μας έδωσαν τις αφορμές, οι ίδιες οι διαπιστώσεις και οι ανάγκες από τις φυσικές καταστάσεις. Περιληπτικά: έτσι, ζευγαρωμένα, ο Νεύτων ανέπτυξε τη Μηχανική και τον Απειροστικό Λογισμό. Γι’ αυτό και, παρ’ ότι είχε την ουσιαστική ακριβολογία του μεγάλου, ο Απειροστικός του ήταν κυριαρχημένος από την κινητική θεώρηση σε βαθμό, που (με την ορμή που εμπνέουν, και τη συγκομιδή ορθών ή όχι αποτελεσμάτων, που χαρίζουν, οι διαισθητικοί τρόποι) ανέστειλε για δύο αιώνες την ανάσταση της απόλυτα αυστηρής "στατικής" θεωρήσεως εννοιών του Απειροστικού από κορυφαίους αρχαίους Έλληνες μαθηματικούς (Εύδοξος, Αρχιμήδης, …….)»
με εκτίμηση
Γιάννης Κερασαρίδης
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
16ο ΣΗΜΕΙΩΜΑ
Προλεγόμενα Με το σημείωμα τούτο δημοσιεύουμε τη δεύτερη συνέχεια του 15ου σημειώματος. Υπενθυμίζουμε πως τα πήραμε από διάλεξη του ομότιμου καθηγητή του ΕΚΠΑ Σπύρου Ζερβού.
Χρήσιμα Μαθηματικά
«ΕΡΩΤΗΜΑ: Ποια Μαθηματικά έχουν, στην πράξη, φανεί τα πιο χρήσιμα στις φυσικές επιστήμες;
ΑΠΑΝΤΗΣΗ: Ιδιαιτέρως από το τέλος του 19ου αιώνα και πέρα, Μαθηματικά, που είχαν γίνει χωρίς την παραμικρή υποψία ότι θα βρίσκανε κάποιες εφαρμογές! Η ερμηνεία του "παράδοξου" αυτού βρίσκεται, ίσως, στο ότι, κατά κανόνα, αξίζουνε περισσότερο τα πράγματα, που γίνονται από εσωτερική παρόρμηση του ερευνητή από εκείνα, που γίνονται "κατά παραγγελία" (στο πλαίσιο κάποιου "ερευνητικού προγράμματος", στη σημερινή γλώσσα)˙ ακριβώς, όπως στα εργόχειρα του παλιού καιρού, που βρίσκονται στα μουσεία, αξίζουνε πολύ περισσότερο από τα σχέδια, που ετοιμάζει κάποιος σημερινός τεχνικός βιοτεχνίας για την τουριστική αγορά˙ και όπως η δουλειά του παλιού μερακλή μαραγκού, από τα σημερινά προκάτ»
«ΕΡΩΤΗΜΑ: Πως πρέπει να αντιμετωπίζουμε τα ήδη χρησιμοποιημένα στις φυσικές επιστήμες Μαθηματικά, ως προς αυτές;
ΑΠΑΝΤΗΣΗ: Με δημιουργικά κριτικό πνεύμα˙ ούτε σαν υποχρεωτικώς "ιερά", ούτε σαν οπωσδήποτε "ξεπερασμένα". Συγκεκριμένα: α) αν είναι ανακριβή, αλλά, στην πράξη, λειτουργούν, θα πρέπει να υπάρχει, κρυμμένη πίσω από τις ανακριβείς διατυπώσεις, κάποια σωστή μαθηματική θεωρία, σε ανταπόκριση (του είδους, που περιγράψαμε˙ είμαστε στο "σαν", πάντοτε) με την φυσική πραγματικότητα. Λόγω αυτής της (πλαίσιο, που είπαμε) σχετικώς αρμονικής συνδέσεως σωστών Μαθηματικών και Φυσικής, λειτουργούν. Η αναζήτηση των σωστών, αλλά και, φυσικά γόνιμων, αυτών Μαθηματικών, προϋποθέτει την πλατιά και βαθιά μαθηματική παιδεία, ορίζοντες επιστημονικούς ανοικτούς και γνήσια αίσθηση της φυσικής πραγματικότητας. Το πιο γνωστό παράδειγμα στα τελευταία πενήντα χρόνια είναι, το πώς, από τα "τρελά" Μαθηματικά ενός πρωτοπόρου μηχανικού, του Χέβισάιντ και ενός μεγάλου θεωρητικού φυσικού, του Ντιράκ, βγάλανε σωστές και γόνιμες θεωρίες μαθηματικοί μεγάλοι, όπως ο Ρώσος Σομπόλεφ και, προ παντός, ο Γάλλος Λωράν Σβάρτζ. Οι επιπτώσεις των θεωριών αυτών ξεπέρασαν αφάνταστα τον αρχικό προορισμό τους. Αυτό χαρακτηρίζει τα γόνιμα Μαθηματικά»
ΠΡΟΑΓΓΕΛΙΑ: Στο επόμενο θα δημοσιεύσουμε μερικά αποσπάσματα από τη συνομιλία μεταξύ του διακεκριμένου μοριακού βιολόγου Jean-Pierre Changeux και του, επίσης διακεκριμένου μαθηματικού, Alain Connes με θέμα την χρησιμότητα των μαθηματικών μοντέλων στη βιολογία.
με εκτίμηση
Γιάννης Κερασαρίδης
Προλεγόμενα Με το σημείωμα τούτο δημοσιεύουμε τη δεύτερη συνέχεια του 15ου σημειώματος. Υπενθυμίζουμε πως τα πήραμε από διάλεξη του ομότιμου καθηγητή του ΕΚΠΑ Σπύρου Ζερβού.
Χρήσιμα Μαθηματικά
«ΕΡΩΤΗΜΑ: Ποια Μαθηματικά έχουν, στην πράξη, φανεί τα πιο χρήσιμα στις φυσικές επιστήμες;
ΑΠΑΝΤΗΣΗ: Ιδιαιτέρως από το τέλος του 19ου αιώνα και πέρα, Μαθηματικά, που είχαν γίνει χωρίς την παραμικρή υποψία ότι θα βρίσκανε κάποιες εφαρμογές! Η ερμηνεία του "παράδοξου" αυτού βρίσκεται, ίσως, στο ότι, κατά κανόνα, αξίζουνε περισσότερο τα πράγματα, που γίνονται από εσωτερική παρόρμηση του ερευνητή από εκείνα, που γίνονται "κατά παραγγελία" (στο πλαίσιο κάποιου "ερευνητικού προγράμματος", στη σημερινή γλώσσα)˙ ακριβώς, όπως στα εργόχειρα του παλιού καιρού, που βρίσκονται στα μουσεία, αξίζουνε πολύ περισσότερο από τα σχέδια, που ετοιμάζει κάποιος σημερινός τεχνικός βιοτεχνίας για την τουριστική αγορά˙ και όπως η δουλειά του παλιού μερακλή μαραγκού, από τα σημερινά προκάτ»
«ΕΡΩΤΗΜΑ: Πως πρέπει να αντιμετωπίζουμε τα ήδη χρησιμοποιημένα στις φυσικές επιστήμες Μαθηματικά, ως προς αυτές;
ΑΠΑΝΤΗΣΗ: Με δημιουργικά κριτικό πνεύμα˙ ούτε σαν υποχρεωτικώς "ιερά", ούτε σαν οπωσδήποτε "ξεπερασμένα". Συγκεκριμένα: α) αν είναι ανακριβή, αλλά, στην πράξη, λειτουργούν, θα πρέπει να υπάρχει, κρυμμένη πίσω από τις ανακριβείς διατυπώσεις, κάποια σωστή μαθηματική θεωρία, σε ανταπόκριση (του είδους, που περιγράψαμε˙ είμαστε στο "σαν", πάντοτε) με την φυσική πραγματικότητα. Λόγω αυτής της (πλαίσιο, που είπαμε) σχετικώς αρμονικής συνδέσεως σωστών Μαθηματικών και Φυσικής, λειτουργούν. Η αναζήτηση των σωστών, αλλά και, φυσικά γόνιμων, αυτών Μαθηματικών, προϋποθέτει την πλατιά και βαθιά μαθηματική παιδεία, ορίζοντες επιστημονικούς ανοικτούς και γνήσια αίσθηση της φυσικής πραγματικότητας. Το πιο γνωστό παράδειγμα στα τελευταία πενήντα χρόνια είναι, το πώς, από τα "τρελά" Μαθηματικά ενός πρωτοπόρου μηχανικού, του Χέβισάιντ και ενός μεγάλου θεωρητικού φυσικού, του Ντιράκ, βγάλανε σωστές και γόνιμες θεωρίες μαθηματικοί μεγάλοι, όπως ο Ρώσος Σομπόλεφ και, προ παντός, ο Γάλλος Λωράν Σβάρτζ. Οι επιπτώσεις των θεωριών αυτών ξεπέρασαν αφάνταστα τον αρχικό προορισμό τους. Αυτό χαρακτηρίζει τα γόνιμα Μαθηματικά»
ΠΡΟΑΓΓΕΛΙΑ: Στο επόμενο θα δημοσιεύσουμε μερικά αποσπάσματα από τη συνομιλία μεταξύ του διακεκριμένου μοριακού βιολόγου Jean-Pierre Changeux και του, επίσης διακεκριμένου μαθηματικού, Alain Connes με θέμα την χρησιμότητα των μαθηματικών μοντέλων στη βιολογία.
με εκτίμηση
Γιάννης Κερασαρίδης
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
17ο ΣΗΜΕΙΩΜΑ
Προλεγόμενα Συνεχίζουμε τα σημειώματα σχετικά με το θέμα μας. Στο σημείωμα τούτο μεταφέρουμε, αυτούσια, τη συνομιλία μεταξύ του διακεκριμένου μοριακού βιολόγου Jean-Pierre Changeux και του, επίσης διακεκριμένου μαθηματικού, Alain Connes με θέμα την χρησιμότητα των μαθηματικών μοντέλων στη βιολογία. Ο διάλογος θα δοθεί σε δυο συνέχειες [πηγή: Jean-Pierre Changeux, Alain Connes: «ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ Ο ΕΓΚΕΦΑΛΟΣ», εκδ. ΚΑΤΟΠΤΡΟ, Αθήνα 1995]
Η χρησιμότητα των μαθηματικών μοντέλων στη βιολογία
JPC: Η πίστη στις εξηγητικές αρετές των μαθηματικών μοντέλων συναντάται σπανιότερα μεταξύ των βιολόγων. Για μας, τα Μαθηματικά χρησιμεύουν σε δύο κυρίως πράγματα. Το πρώτο είναι η ανάλυση των πειραματικών δεδομένων….
AC: Αυτό είναι Στατιστική
JPC: Ναι, η εξαγωγή των δεδομένων. Ένας υπολογιστής μπορεί να κάνει αυτή την εργασία αυτομάτως, χωρίς να χρειάζεται να προσφεύγει στον εγκέφαλο του πειραματιστή. Στη συνέχεια, τα Μαθηματικά μας βοηθούν να κατασκευάζουμε κάποια θεωρητικά μοντέλα, η επεξεργασία των οποίων ξεκινά από τα δεδομένα του πειράματος, όπως και στη Φυσική. Καθορίζονται κάποιες παραδοχές οι οποίες μπορεί να είναι, λόγου χάρη στην περίπτωση της διάδοσης της νευρικής ώσης, η μέτρηση της μεταβολής του ηλεκτρικού δυναμικού σ’ ένα δεδομένο σημείο ενός νεύρου και η μέτρηση των ρευμάτων που μεταφέρονται από τα ιόντα Νατρίου και Καλίου συναρτήσει του δυναμικού. Ο Hodgkin και Huxley πρότειναν μια εξίσωση η οποία βάσει των εν λόγω παραδοχών εκφράζει τις ιοντικές βάσεις της νευρικής ώσης. Αυτή η εξίσωση μας επιτρέπει να περιγράψουμε το φαινόμενο και να το "ανασυγκροτήσουμε" ξεκινώντας από κάποια στοιχειώδη δεδομένα.
AC: Είναι μια μέθοδος να κωδικεύουμε την πληροφορία…
JPC: Και κυρίως να την ανασυγκροτούμε
AC: Είναι, λοιπόν, κατά κάποιο τρόπο, σαν μια γλώσσα, αφού μια γλώσσα υπάρχει για να αναπαράγει……
JPC:Βέβαια. Επιτρέπει την αναπαραγωγή, αλλά έχει επίσης κι ένα προβλεπτικό χαρακτήρα. Ωστόσο, κανένας βιολόγος, απ’ όσο γνωρίζω, δεν θα έλεγε ότι η εξίσωση των Hodgkin και Huxley ταυτίζεται με τη νευρική ώση, ούτε βέβαια πως διατάσσει τη διάδοσή της. Αυτό που υπαγορεύει τη διάδοση της νευρικής ώσης δεν είναι κάποιος μαθηματικός νόμος του σύμπαντος, όπως αρέσει σε ορισμένους φυσικούς να λένε, μιλώντας για την εργασία τους!
Προλεγόμενα Συνεχίζουμε τα σημειώματα σχετικά με το θέμα μας. Στο σημείωμα τούτο μεταφέρουμε, αυτούσια, τη συνομιλία μεταξύ του διακεκριμένου μοριακού βιολόγου Jean-Pierre Changeux και του, επίσης διακεκριμένου μαθηματικού, Alain Connes με θέμα την χρησιμότητα των μαθηματικών μοντέλων στη βιολογία. Ο διάλογος θα δοθεί σε δυο συνέχειες [πηγή: Jean-Pierre Changeux, Alain Connes: «ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ Ο ΕΓΚΕΦΑΛΟΣ», εκδ. ΚΑΤΟΠΤΡΟ, Αθήνα 1995]
Η χρησιμότητα των μαθηματικών μοντέλων στη βιολογία
JPC: Η πίστη στις εξηγητικές αρετές των μαθηματικών μοντέλων συναντάται σπανιότερα μεταξύ των βιολόγων. Για μας, τα Μαθηματικά χρησιμεύουν σε δύο κυρίως πράγματα. Το πρώτο είναι η ανάλυση των πειραματικών δεδομένων….
AC: Αυτό είναι Στατιστική
JPC: Ναι, η εξαγωγή των δεδομένων. Ένας υπολογιστής μπορεί να κάνει αυτή την εργασία αυτομάτως, χωρίς να χρειάζεται να προσφεύγει στον εγκέφαλο του πειραματιστή. Στη συνέχεια, τα Μαθηματικά μας βοηθούν να κατασκευάζουμε κάποια θεωρητικά μοντέλα, η επεξεργασία των οποίων ξεκινά από τα δεδομένα του πειράματος, όπως και στη Φυσική. Καθορίζονται κάποιες παραδοχές οι οποίες μπορεί να είναι, λόγου χάρη στην περίπτωση της διάδοσης της νευρικής ώσης, η μέτρηση της μεταβολής του ηλεκτρικού δυναμικού σ’ ένα δεδομένο σημείο ενός νεύρου και η μέτρηση των ρευμάτων που μεταφέρονται από τα ιόντα Νατρίου και Καλίου συναρτήσει του δυναμικού. Ο Hodgkin και Huxley πρότειναν μια εξίσωση η οποία βάσει των εν λόγω παραδοχών εκφράζει τις ιοντικές βάσεις της νευρικής ώσης. Αυτή η εξίσωση μας επιτρέπει να περιγράψουμε το φαινόμενο και να το "ανασυγκροτήσουμε" ξεκινώντας από κάποια στοιχειώδη δεδομένα.
AC: Είναι μια μέθοδος να κωδικεύουμε την πληροφορία…
JPC: Και κυρίως να την ανασυγκροτούμε
AC: Είναι, λοιπόν, κατά κάποιο τρόπο, σαν μια γλώσσα, αφού μια γλώσσα υπάρχει για να αναπαράγει……
JPC:Βέβαια. Επιτρέπει την αναπαραγωγή, αλλά έχει επίσης κι ένα προβλεπτικό χαρακτήρα. Ωστόσο, κανένας βιολόγος, απ’ όσο γνωρίζω, δεν θα έλεγε ότι η εξίσωση των Hodgkin και Huxley ταυτίζεται με τη νευρική ώση, ούτε βέβαια πως διατάσσει τη διάδοσή της. Αυτό που υπαγορεύει τη διάδοση της νευρικής ώσης δεν είναι κάποιος μαθηματικός νόμος του σύμπαντος, όπως αρέσει σε ορισμένους φυσικούς να λένε, μιλώντας για την εργασία τους!
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
18ο ΣΗΜΕΙΩΜΑ
Προλεγόμενα Το κείμενο τούτο αποτελεί τη συνέχεια του 17ου σημειώματος. Αναφέρεται στην εξίσωση των Hodgkin και Huxley. Εμείς θα παραθέσουμε μερικές γραμμές, επεξηγηματικές των εννοιών «εξίσωση των Hodgkin και Huxley».
Η εξίσωση των Hodgkin και Huxley
«AC: Πιστεύω ότι σ’ αυτό το σημείο θέτεις ένα πολύ συγκεκριμένο ζήτημα. Αν προχωρήσουμε στην ανάλυση, ας πούμε χημική και ηλεκτρική, του φαινομένου, υποθέτω ότι χάρη στους νόμους της χημείας θα καταλήξουμε να αποδείξουμε την εν λόγω εξίσωση.
JPC: Πρόκειται για ένα πολύ σημαντικό ζήτημα. Αυτή η μαθηματική εξίσωση μπορεί να εξηγηθεί περαιτέρω, τουλάχιστον εν μέρει, από τις υποκείμενες μοριακές διαδικασίες. Το μόριο που περιέχει το ευαίσθητο στη διαφορά δυναμικού κανάλι, μέσα από το οποίο περνούν τα ιόντα νατρίου, έχει απομονωθεί στο εργαστήριο, το δε νουκλεϊκό οξύ που το κωδικεύει έχει κλωνοποιηθεί και έχει προσδιοριστεί η αλληλουχία των νουκλεοτιδίων του . Έχουμε πλέον στα χέρια μας τους μοριακούς μηχανισμούς που καθορίζουν τη διάδοση της νευρικής ώσης. Ωστόσο, αξίζει να σημειωθεί πως ούτε οι ηλεκτροφυσιολογικές καταγραφές ούτε η μαθηματική εξίσωση που τις περιγράφει μας επέτρεψαν να έχουμε άμεση πρόσβαση στη στοιχειώδη μοριακή δομή που εξηγεί τελικά το φαινόμενο. Η πρόσβαση σ’ αυτή τη δομή έγινε εφικτή μέσω μιας πολύ διαφορετικής προσέγγισης, η οποία στηρίζεται στις μεθόδους της βιοχημείας και της μοριακής βιολογίας. Η μαθηματική εξίσωση για τη διάδοση της νευρικής ώσης βασίζεται σε έναν αριθμό προτάσεων που αφορούν τα κανάλια η ύπαρξη των οποίων προϋποτίθεται απ’ αυτό το μοντέλο. Η εξίσωση αυτή, βέβαια, ορίζει έναν ορισμένο αριθμό στοιχειωδών ιοντικών ιδιοτήτων τις οποίες πρέπει να παρουσιάζει το "υπεύθυνο" μόριο. Δεν μας λέει, όμως, αν αυτά τα κανάλια είναι πρωτεΐνες ή λιπίδια. Η εξίσωση αναφέρεται σε συνεργασιακά φαινόμενα που λαμβάνουν χώρα στο επίπεδο της κυτταρικής μεμβράνης και της μεταφοράς ιόντων. Επίσης δεν μας λέει ποιος πρέπει να είναι ο ακριβής αριθμός των εμπλεκόμενων υπομονάδων ή των πρωτεϊνών που συμμετέχουν στο παιχνίδι. Τα Μαθηματικά έχουν για μας τους βιολόγουςμια σίγουρη αλλά περιορισμένη ροβλεπτική λειτουργία. Δεν μας επιτρέπουν την απευθείας πρόσβαση στις δομές………»
Επεξηγήσεις για το μοντέλο των Hodgkin και Huxley
[πηγή: "Διπλωματική Εργασία", Ιωάννας Δ. Χροναίου, με θέμα «Προσομοίωση της φυσιολογίας των βασικών γαγγλίων στη νόσο του Πάρκινσον μέσω ενός λεπτομερούς πολυεπίπεδου υπολογιστικού μοντέλου». Ε.Μ.Π., 2011]
Το μοντέλο αυτό περιγράφεται από τις παρακάτω απλές βασικές εξισώσεις:
―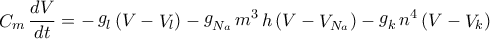
―
―
―
[Κ. Σ. Νικήτα (2011). Προσομοίωση Φυσιολογικών Συστημάτων. Αθήνα: Εκδόσεις Τζιόλα.]
Πρόκειται για ένα σύστημα τεσσάρων γραμμικών συνήθων διαφορικών εξισώσεων με μία ανεξάρτητη μεταβλητή, το χρόνο, και τέσσερες εξαρτημένες μεταβλητές, το δυναμικό V και τις μεταβλητές κατάστασης (ανοιχτής ή κλειστής) των πυλών m (πύλη ενεργοποίησης του Na+), h (πύλη απενεργοποίησης Na+) και n (πύλη ενεργοποίησης Κ+). Οι συναρτήσεις a και b εκφράζουν τους ρυθμούς με τους οποίους η πύλη περνά από την κλειστή στην ανοιχτή κατάσταση και από την ανοιχτή στην κλειστή κατάσταση, αντίστοιχα. Οι Hodgkin και Huxley τις υπολόγισαν για κάθε πύλη. Οι παράμετροι του μοντέλου είναι οι μέγιστες αγωγιμότητες των ενεργητικών καναλιών Na+(gNa) και K+(gk), τα δυναμικά ισορροπίας Na+(gNa) και K+(gk), η αγωγιμότητα διαρροής (gl), το δυναμικό διαρροής (VL) και η ισοδύναμη χωρητικότητα της μεμβράνης Cm. Αξίζει να παρατηρηθεί ότι όλοι οι όροι του δεξιού μέρους της πρώτης εξίσωσης εκφράζουν ρεύματα, των οποίων η ένταση για τα ενεργητικά κανάλια διαμορφώνεται από τις τιμές των μεταβλητών των πυλών.
ΣΗΜΕΙΩΣΗ:
Επειδή την επόμενη εβδομάδα (1/10 - 6/10) θα είμαστε εκτός Ελλάδας, η συνέχεια των σημειωμάτων θα πραγματοποιηθεί την μεθεπόμενη εβδομάδα
με εκτίμηση
Γιάννης Κερασαρίδης
Προλεγόμενα Το κείμενο τούτο αποτελεί τη συνέχεια του 17ου σημειώματος. Αναφέρεται στην εξίσωση των Hodgkin και Huxley. Εμείς θα παραθέσουμε μερικές γραμμές, επεξηγηματικές των εννοιών «εξίσωση των Hodgkin και Huxley».
Η εξίσωση των Hodgkin και Huxley
«AC: Πιστεύω ότι σ’ αυτό το σημείο θέτεις ένα πολύ συγκεκριμένο ζήτημα. Αν προχωρήσουμε στην ανάλυση, ας πούμε χημική και ηλεκτρική, του φαινομένου, υποθέτω ότι χάρη στους νόμους της χημείας θα καταλήξουμε να αποδείξουμε την εν λόγω εξίσωση.
JPC: Πρόκειται για ένα πολύ σημαντικό ζήτημα. Αυτή η μαθηματική εξίσωση μπορεί να εξηγηθεί περαιτέρω, τουλάχιστον εν μέρει, από τις υποκείμενες μοριακές διαδικασίες. Το μόριο που περιέχει το ευαίσθητο στη διαφορά δυναμικού κανάλι, μέσα από το οποίο περνούν τα ιόντα νατρίου, έχει απομονωθεί στο εργαστήριο, το δε νουκλεϊκό οξύ που το κωδικεύει έχει κλωνοποιηθεί και έχει προσδιοριστεί η αλληλουχία των νουκλεοτιδίων του . Έχουμε πλέον στα χέρια μας τους μοριακούς μηχανισμούς που καθορίζουν τη διάδοση της νευρικής ώσης. Ωστόσο, αξίζει να σημειωθεί πως ούτε οι ηλεκτροφυσιολογικές καταγραφές ούτε η μαθηματική εξίσωση που τις περιγράφει μας επέτρεψαν να έχουμε άμεση πρόσβαση στη στοιχειώδη μοριακή δομή που εξηγεί τελικά το φαινόμενο. Η πρόσβαση σ’ αυτή τη δομή έγινε εφικτή μέσω μιας πολύ διαφορετικής προσέγγισης, η οποία στηρίζεται στις μεθόδους της βιοχημείας και της μοριακής βιολογίας. Η μαθηματική εξίσωση για τη διάδοση της νευρικής ώσης βασίζεται σε έναν αριθμό προτάσεων που αφορούν τα κανάλια η ύπαρξη των οποίων προϋποτίθεται απ’ αυτό το μοντέλο. Η εξίσωση αυτή, βέβαια, ορίζει έναν ορισμένο αριθμό στοιχειωδών ιοντικών ιδιοτήτων τις οποίες πρέπει να παρουσιάζει το "υπεύθυνο" μόριο. Δεν μας λέει, όμως, αν αυτά τα κανάλια είναι πρωτεΐνες ή λιπίδια. Η εξίσωση αναφέρεται σε συνεργασιακά φαινόμενα που λαμβάνουν χώρα στο επίπεδο της κυτταρικής μεμβράνης και της μεταφοράς ιόντων. Επίσης δεν μας λέει ποιος πρέπει να είναι ο ακριβής αριθμός των εμπλεκόμενων υπομονάδων ή των πρωτεϊνών που συμμετέχουν στο παιχνίδι. Τα Μαθηματικά έχουν για μας τους βιολόγουςμια σίγουρη αλλά περιορισμένη ροβλεπτική λειτουργία. Δεν μας επιτρέπουν την απευθείας πρόσβαση στις δομές………»
Επεξηγήσεις για το μοντέλο των Hodgkin και Huxley
[πηγή: "Διπλωματική Εργασία", Ιωάννας Δ. Χροναίου, με θέμα «Προσομοίωση της φυσιολογίας των βασικών γαγγλίων στη νόσο του Πάρκινσον μέσω ενός λεπτομερούς πολυεπίπεδου υπολογιστικού μοντέλου». Ε.Μ.Π., 2011]
Το μοντέλο αυτό περιγράφεται από τις παρακάτω απλές βασικές εξισώσεις:
―
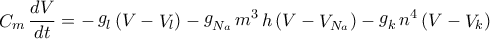
―

―

―

[Κ. Σ. Νικήτα (2011). Προσομοίωση Φυσιολογικών Συστημάτων. Αθήνα: Εκδόσεις Τζιόλα.]
Πρόκειται για ένα σύστημα τεσσάρων γραμμικών συνήθων διαφορικών εξισώσεων με μία ανεξάρτητη μεταβλητή, το χρόνο, και τέσσερες εξαρτημένες μεταβλητές, το δυναμικό V και τις μεταβλητές κατάστασης (ανοιχτής ή κλειστής) των πυλών m (πύλη ενεργοποίησης του Na+), h (πύλη απενεργοποίησης Na+) και n (πύλη ενεργοποίησης Κ+). Οι συναρτήσεις a και b εκφράζουν τους ρυθμούς με τους οποίους η πύλη περνά από την κλειστή στην ανοιχτή κατάσταση και από την ανοιχτή στην κλειστή κατάσταση, αντίστοιχα. Οι Hodgkin και Huxley τις υπολόγισαν για κάθε πύλη. Οι παράμετροι του μοντέλου είναι οι μέγιστες αγωγιμότητες των ενεργητικών καναλιών Na+(gNa) και K+(gk), τα δυναμικά ισορροπίας Na+(gNa) και K+(gk), η αγωγιμότητα διαρροής (gl), το δυναμικό διαρροής (VL) και η ισοδύναμη χωρητικότητα της μεμβράνης Cm. Αξίζει να παρατηρηθεί ότι όλοι οι όροι του δεξιού μέρους της πρώτης εξίσωσης εκφράζουν ρεύματα, των οποίων η ένταση για τα ενεργητικά κανάλια διαμορφώνεται από τις τιμές των μεταβλητών των πυλών.
ΣΗΜΕΙΩΣΗ:
Επειδή την επόμενη εβδομάδα (1/10 - 6/10) θα είμαστε εκτός Ελλάδας, η συνέχεια των σημειωμάτων θα πραγματοποιηθεί την μεθεπόμενη εβδομάδα
με εκτίμηση
Γιάννης Κερασαρίδης
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
19ο ΣΗΜΕΙΩΜΑ
Προλεγόμενα Συνεχίζουμε τα σημειώματά μας για τη φύση και την χρησιμότητα των Μαθηματικών. Γιατί ο βαθμός χρησιμότητάς τους στον άνθρωπο ενισχύει τους λόγους για τους οποίους πρέπει να τα διδάσκουμε στα παιδιά. Επιλέξαμε τον τομέα "ΟΙΚΟΝΟΜΙΑ" και τον λόγο ενός φιλοσόφου των Μαθηματικών, του Moshé Flato. Η περικοπή θα δημοσιευθεί σε δύο σημειώματα.
Τα Μαθηματικά στην Οικονομία
Όταν προσεγγίζει κανείς συλλογικά φαινόμενα, εκδηλώνεται εξίσου έντονα η ίδια ελπίδα, αλλά θα πρέπει να εκφράσουμε μια ακόμη πιο σταθερή επιφύλαξη. Το πιο διδακτικό παράδειγμα είναι σίγουρα εκείνο της οικονομίας, διότι σε αυτόν τον τομέα έχουν πραγματοποιηθεί σοβαρές απόπειρες μαθηματικοποίησης, για τις οποίες μπορούμε να συζητήσουμε σε στέρεες βάσεις. Όμως, τι έχουν κάνει οι οικονομολόγοι; Σύμφωνα με τον Ρaul Samuelson, δανείστηκαν κατ' ουσίαν τους νόμους της θερμοδυναμικής που διέπουν την εξέλιξη των φυσικών συστημάτων, μεταφέροντάς τους στα δικά τους αντικείμενα. Αυτή η μεταφορά, που βαφτίστηκε «εφαρμογή», τους επέτρεψε να δώσουν ορισμούς της «συνάρτησης ωφελιμότητας», του «κεφαλαίου» κ.λ.π. Έτσι, είδαμε να αναδύονται πολυάριθμα «μοντέλα» στη μικροοικονομία και στη μακροοικονομία. Οι απόπειρες αυτές προχώρησαν πολύ περισσότερο απ' ό,τι συχνά πιστεύουμε σήμερα. Χρησιμοποιείται ευρύτατα η μηχανική του Lagrange, δηλαδή η κλασική μηχανική στη συστηματοποιημένη μορφή της, και ο λογισμός των μεταβολών, σε μεγάλη έκταση. Ο γάλλος μαθηματικός Gérard Debreu του Πανεπιστημίου της Καλιφόρνιας, στο Μπέρκλεϋ, κέρδισε το βραβείο Νόμπελ για μια μαθηματική θεωρία της οικονομίας, ενώ ο ιταλός Franco Modigliani του ΜΙΤ για την κατασκευή ενός μαθηματικού μοντέλου των χρηματοπιστωτικών αγορών. 'Έγινε επίσης απόπειρα να εφαρμοστεί η θεωρία καταστροφών του René Thom σε φαινόμενα «ιδιομορφιών» σε αυτήν την περιοχή. Όμως, το ζήτημα του κατά πόσο τα μοντέλα αυτά έχουν κάποια επαληθευμένη σχέση με την πραγματικότητα παραμένει τουλάχιστον ανοιχτό. Δεν είναι άραγε ακόμη πολύ πρωτόγονα; [πηγή: Moshé Flato, “Η ΙΣΧΥΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ”, εκδ. ΚΑΤΟΠΤΡΟ, Αθήνα 1993]
με εκτίμηση
Γιάννης Κερασαρίδης
Προλεγόμενα Συνεχίζουμε τα σημειώματά μας για τη φύση και την χρησιμότητα των Μαθηματικών. Γιατί ο βαθμός χρησιμότητάς τους στον άνθρωπο ενισχύει τους λόγους για τους οποίους πρέπει να τα διδάσκουμε στα παιδιά. Επιλέξαμε τον τομέα "ΟΙΚΟΝΟΜΙΑ" και τον λόγο ενός φιλοσόφου των Μαθηματικών, του Moshé Flato. Η περικοπή θα δημοσιευθεί σε δύο σημειώματα.
Τα Μαθηματικά στην Οικονομία
Όταν προσεγγίζει κανείς συλλογικά φαινόμενα, εκδηλώνεται εξίσου έντονα η ίδια ελπίδα, αλλά θα πρέπει να εκφράσουμε μια ακόμη πιο σταθερή επιφύλαξη. Το πιο διδακτικό παράδειγμα είναι σίγουρα εκείνο της οικονομίας, διότι σε αυτόν τον τομέα έχουν πραγματοποιηθεί σοβαρές απόπειρες μαθηματικοποίησης, για τις οποίες μπορούμε να συζητήσουμε σε στέρεες βάσεις. Όμως, τι έχουν κάνει οι οικονομολόγοι; Σύμφωνα με τον Ρaul Samuelson, δανείστηκαν κατ' ουσίαν τους νόμους της θερμοδυναμικής που διέπουν την εξέλιξη των φυσικών συστημάτων, μεταφέροντάς τους στα δικά τους αντικείμενα. Αυτή η μεταφορά, που βαφτίστηκε «εφαρμογή», τους επέτρεψε να δώσουν ορισμούς της «συνάρτησης ωφελιμότητας», του «κεφαλαίου» κ.λ.π. Έτσι, είδαμε να αναδύονται πολυάριθμα «μοντέλα» στη μικροοικονομία και στη μακροοικονομία. Οι απόπειρες αυτές προχώρησαν πολύ περισσότερο απ' ό,τι συχνά πιστεύουμε σήμερα. Χρησιμοποιείται ευρύτατα η μηχανική του Lagrange, δηλαδή η κλασική μηχανική στη συστηματοποιημένη μορφή της, και ο λογισμός των μεταβολών, σε μεγάλη έκταση. Ο γάλλος μαθηματικός Gérard Debreu του Πανεπιστημίου της Καλιφόρνιας, στο Μπέρκλεϋ, κέρδισε το βραβείο Νόμπελ για μια μαθηματική θεωρία της οικονομίας, ενώ ο ιταλός Franco Modigliani του ΜΙΤ για την κατασκευή ενός μαθηματικού μοντέλου των χρηματοπιστωτικών αγορών. 'Έγινε επίσης απόπειρα να εφαρμοστεί η θεωρία καταστροφών του René Thom σε φαινόμενα «ιδιομορφιών» σε αυτήν την περιοχή. Όμως, το ζήτημα του κατά πόσο τα μοντέλα αυτά έχουν κάποια επαληθευμένη σχέση με την πραγματικότητα παραμένει τουλάχιστον ανοιχτό. Δεν είναι άραγε ακόμη πολύ πρωτόγονα; [πηγή: Moshé Flato, “Η ΙΣΧΥΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ”, εκδ. ΚΑΤΟΠΤΡΟ, Αθήνα 1993]
με εκτίμηση
Γιάννης Κερασαρίδης
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
20ο ΣΗΜΕΙΩΜΑ
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΟΙΚΟΝΟΜΙΑ 2
Προλεγόμενα: Συνεχίζουμε με το δεύτερο μέρος για τη σχέση Οικονομίας και Μαθηματικών, όπως τη βλέπει ένας φιλόσοφος των Μαθηματικών, ο Moshé Flato.
«Πώς είναι δυνατό, για παράδειγμα, να μη σημειώσουμε ότι ψυχολογικοί παράγοντες που συνδέονται με τη συμπεριφορά των οικονομικών «φορέων» κλονίζουν την καθαρότητα και την αποτελεσματικότητα αυτών των μοντέλων; Να, λοιπόν, κάτι που σίγουρα δεν διέφυγε από τους ειδικούς που προσπάθησαν να εφαρμόσουν τη θεωρία παιγνίων σε αυτήν τη συμπεριφορά, προκειμένου να μειώσουν τα διαταρακτικά φαινόμενα που προκαλεί. Προφανώς όμως, η θεωρία παιγνίων, η οποία είναι μια πανέμορφη μαθηματική θεωρία που θεμελιώθηκε το 1944 από τον John von Neumann και τον Oskar Morgenstern, δεν αρκεί για να συλλάβει κανείς όλες τις παραμέτρους, διότι για λόγους αρχής οφείλει να υποθέσει πως το άτομο ακολουθεί κάθε στιγμή τη βέλτιστη στρατηγική που υπαγορεύει το συμφέρον του. Πράγμα που εμφανώς δεν συμβαίνει!
Η στατιστική μπορεί λοιπόν, χωρίς αμφιβολία, να διατηρήσει τη χρησιμότητά της ως μέσο επαλήθευσης ή επιβεβαίωσης ορισμένων υποθέσεων, είναι όμως ακόμη πολύ νωρίς για να εγκατασταθεί στην οικονομική επιστήμη μια πραγματική «εξουσία» των μαθηματικών, με τον τρόπο που έχει γίνει στη φυσική. Η κατάσταση είναι εδώ συγκρίσιμη με εκείνη της βιολογίας: τα συστήματα που επιθυμούμε να μαθηματικοποιήσουμε είναι υπερβολικά πολύπλοκα και εμπεριέχουν υπερβολικά πολλές παραμέτρους, ώστε δεν μπορούμε να τα κατανοήσουμε με ορθό τρόπο. Δεν αρκεί όμως να αποφανθεί κανείς ότι φταίει ο περιορισμένος αριθμός των παραμέτρων και να ξεκινήσει αμέσως το κυνήγι των «λανθανουσών παραμέτρων». Η κατάσταση είναι εδώ πολύ πιο σοβαρή: αφού έχουμε να κάνουμε με συστήματα όπου υπεισέρχονται όντα εφοδιασμένα με εγκέφαλο που μπορούν να έχουν πολλαπλότητα αποφάσεων, οι οποίες διαταράσσουν τον τρόπο λειτουργίας των συστημάτων, δεν γνωρίζουμε ακόμη πως να τα αποδώσουμε εννοιολογικά. Έτσι λοιπόν, επειδή ουσιαστικά η ίδια η οικονομική θεωρία πάσχει από έλλειμμα εννοιολογικής απόδοσης, η αποτελεσματικότητα των μαθηματικών είναι προς το παρόν πολύ περιορισμένη σ' αυτόν τον τομέα. Θα καλυφθεί άραγε στα χρόνια που έρχονται αυτό το εννοιολογικό έλλειμμα; Έχουμε κάθε λόγο να ελπίζουμε. Τότε θα δούμε αν επαρκούν για το στόχο αυτό τα μαθηματικά όπως υπάρχουν σήμερα, ή αν χρειάζεται να αναπτυχθούν άλλοι τύποι μαθηματικών, άλλοι τρόποι σκέψης, προσαρμοσμένοι σε τούτες τις ειδικές μορφές αλληλεπίδρασης, οι οποίοι πιθανώς θα συμπληρώσουν και θα εμπλουτίσουν εκείνους που διαθέτουμε προς το παρόν.
Όσα μόλις παραθέσαμε σχετικά με την οικονομία, μπορεί να ισχύουν και αναφορικά με το σύνολο των κοινωνικών επιστημών που «αλληθωρίζουν» προς τα μαθηματικά. Τα ίδια βασικά επιχειρήματα θα έδειχναν ταυτόχρονα ότι οι ελπίδες τους είναι δικαιολογημένες, αλλά και ότι οι αλαλαγμοί νίκης που ακούγονται είναι ακόμη πρόωροι»
[πηγή: Moshé Flato, “Η ΙΣΧΥΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ”, εκδ. ΚΑΤΟΠΤΡΟ, Αθήνα 1993]
με εκτίμηση
Γιάννης Κερασαρίδης
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΟΙΚΟΝΟΜΙΑ 2
Προλεγόμενα: Συνεχίζουμε με το δεύτερο μέρος για τη σχέση Οικονομίας και Μαθηματικών, όπως τη βλέπει ένας φιλόσοφος των Μαθηματικών, ο Moshé Flato.
«Πώς είναι δυνατό, για παράδειγμα, να μη σημειώσουμε ότι ψυχολογικοί παράγοντες που συνδέονται με τη συμπεριφορά των οικονομικών «φορέων» κλονίζουν την καθαρότητα και την αποτελεσματικότητα αυτών των μοντέλων; Να, λοιπόν, κάτι που σίγουρα δεν διέφυγε από τους ειδικούς που προσπάθησαν να εφαρμόσουν τη θεωρία παιγνίων σε αυτήν τη συμπεριφορά, προκειμένου να μειώσουν τα διαταρακτικά φαινόμενα που προκαλεί. Προφανώς όμως, η θεωρία παιγνίων, η οποία είναι μια πανέμορφη μαθηματική θεωρία που θεμελιώθηκε το 1944 από τον John von Neumann και τον Oskar Morgenstern, δεν αρκεί για να συλλάβει κανείς όλες τις παραμέτρους, διότι για λόγους αρχής οφείλει να υποθέσει πως το άτομο ακολουθεί κάθε στιγμή τη βέλτιστη στρατηγική που υπαγορεύει το συμφέρον του. Πράγμα που εμφανώς δεν συμβαίνει!
Η στατιστική μπορεί λοιπόν, χωρίς αμφιβολία, να διατηρήσει τη χρησιμότητά της ως μέσο επαλήθευσης ή επιβεβαίωσης ορισμένων υποθέσεων, είναι όμως ακόμη πολύ νωρίς για να εγκατασταθεί στην οικονομική επιστήμη μια πραγματική «εξουσία» των μαθηματικών, με τον τρόπο που έχει γίνει στη φυσική. Η κατάσταση είναι εδώ συγκρίσιμη με εκείνη της βιολογίας: τα συστήματα που επιθυμούμε να μαθηματικοποιήσουμε είναι υπερβολικά πολύπλοκα και εμπεριέχουν υπερβολικά πολλές παραμέτρους, ώστε δεν μπορούμε να τα κατανοήσουμε με ορθό τρόπο. Δεν αρκεί όμως να αποφανθεί κανείς ότι φταίει ο περιορισμένος αριθμός των παραμέτρων και να ξεκινήσει αμέσως το κυνήγι των «λανθανουσών παραμέτρων». Η κατάσταση είναι εδώ πολύ πιο σοβαρή: αφού έχουμε να κάνουμε με συστήματα όπου υπεισέρχονται όντα εφοδιασμένα με εγκέφαλο που μπορούν να έχουν πολλαπλότητα αποφάσεων, οι οποίες διαταράσσουν τον τρόπο λειτουργίας των συστημάτων, δεν γνωρίζουμε ακόμη πως να τα αποδώσουμε εννοιολογικά. Έτσι λοιπόν, επειδή ουσιαστικά η ίδια η οικονομική θεωρία πάσχει από έλλειμμα εννοιολογικής απόδοσης, η αποτελεσματικότητα των μαθηματικών είναι προς το παρόν πολύ περιορισμένη σ' αυτόν τον τομέα. Θα καλυφθεί άραγε στα χρόνια που έρχονται αυτό το εννοιολογικό έλλειμμα; Έχουμε κάθε λόγο να ελπίζουμε. Τότε θα δούμε αν επαρκούν για το στόχο αυτό τα μαθηματικά όπως υπάρχουν σήμερα, ή αν χρειάζεται να αναπτυχθούν άλλοι τύποι μαθηματικών, άλλοι τρόποι σκέψης, προσαρμοσμένοι σε τούτες τις ειδικές μορφές αλληλεπίδρασης, οι οποίοι πιθανώς θα συμπληρώσουν και θα εμπλουτίσουν εκείνους που διαθέτουμε προς το παρόν.
Όσα μόλις παραθέσαμε σχετικά με την οικονομία, μπορεί να ισχύουν και αναφορικά με το σύνολο των κοινωνικών επιστημών που «αλληθωρίζουν» προς τα μαθηματικά. Τα ίδια βασικά επιχειρήματα θα έδειχναν ταυτόχρονα ότι οι ελπίδες τους είναι δικαιολογημένες, αλλά και ότι οι αλαλαγμοί νίκης που ακούγονται είναι ακόμη πρόωροι»
[πηγή: Moshé Flato, “Η ΙΣΧΥΣ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ”, εκδ. ΚΑΤΟΠΤΡΟ, Αθήνα 1993]
με εκτίμηση
Γιάννης Κερασαρίδης
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
21o ΣΗΜΕΙΩΜΑ
Μοντέλο McCulloch-Pitts
Προλεγόμενα Αρκετοί συνάδελφοι μας ζήτησαν να παρουσιάσουμε κι άλλο ένα θέμα εφαρμογής των Μαθηματικών στην Ιατρική. Εμείς, μεταξύ των άλλων, διαλέξαμε άλλη μία εφαρμογή των Μαθηματικών στη νόσο του PARKINSON. Το κείμενο που ακολουθεί είναι παρμένο από τη διπλωματική εργασία της Αριστέας- Ιωάννας Γ. Φιλντίση. Η Α-Ι Φιλντίση είναι Διπλωματούχος Ηλεκτρολόγος Μηχανικός και Μηχανικός Η/Υ Ε.Μ.Π. Η διπλωματική εργασία φέρει τα παρακάτω στοιχεία:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ Η/Υ - ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ.
Θέμα: ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΔΥΝΑΤΟΤΗΤΑΣ ΠΡΟΒΛΕΨΗΣ ΤΩΝ ΝΕΥΡΩΝΙΚΩΝ ΕΚΠΟΛΩΣΕΩΝ ΑΠΟ ΤΑ ΔΥΝΑΜΙΚΑ ΤΟΠΙΚΟΥ ΠΕΔΙΟΥ.
ΧΡΗΣΗ ΜΙΚΡΟΗΛΕΚΤΡΟΔΙΑΚΩΝ ΚΑΤΑΓΡΑΦΩΝ ΑΠΟ ΤΟΝ ΥΠΟΘΑΛΑΜΙΚΟ ΠΥΡΗΝΑ ΠΑΡΚΙΝΣΟΝΙΚΩΝ ΑΣΘΕΝΩΝ ΠΟΥ ΥΠΟΒΑΛΛΟΝΤΑΙ ΣΕ ΕΝ ΤΩ ΒΑΘΕΙ ΕΓΚΕΦΑΛΙΚΗ ΔΙΕΓΕΡΣΗ
«3.1 Εισαγωγή
Ο εγκέφαλος είναι το πιο πολύπλοκο όργανο του ανθρώπινου οργανισμού. Το χαρακτηριστικό αυτό της πολυπλοκότητας τον καθιστά ικανό να εκτελεί με επιτυχία τις ανώτερες λειτουργίες που συνιστούν αυτό που αποκαλούμε νοημοσύνη. Τέτοιες λειτουργίες είναι η αναγνώριση εικόνων και φωνής, η μνήμη, η λήψη αποφάσεων, η προσαρμογή σε νέες καταστάσεις, η λογική και η μάθηση. Η τελευταία λειτουργία, δηλαδή η μάθηση, είναι ίσως ένα από τα σημαντικότερα χαρακτηριστικά του εγκεφάλου και γενικά των βιολογικών νευρωνικών δικτύων.
Η Τεχνητή Νοημοσύνη υλοποιεί τις παραπάνω λειτουργίες με την υποστήριξη ενός υλικού στρώματος. Στον άνθρωπο και τα ζώα το υλικό αυτό είναι οι νευρώνες, οι οποίοι οργανώνονται σε πυκνά δίκτυα με χιλιάδες συνάψεις ανά νευρώνα. Το αντικείμενο μελέτης της Τεχνητής Νοημοσύνης είναι αφ' ενός η ανάπτυξη ενός υλικού που θα μπορεί να υποστηρίξει τις παραπάνω λειτουργίες, ανεξάρτητα από το αν το υλικό αυτό μιμείται τους νευρώνες ή όχι, αφ' ετέρου η ανάπτυξη αλγορίθμων που θα μιμούνται αυτές τις λειτουργίες.
Ένα τεχνητό νευρωνικό δίκτυο είναι ένα σύστημα επεξεργασίας πληροφορίας που μιμείται τη δομή των βιολογικών νευρώνων και τη λειτουργία των βιολογικών νευρωνικών δικτύων. Η επεξεργασία πληροφορίας των δικτύων αυτών βασίζεται στη μετάδοση σημάτων μεταξύ απλών στοιχείων που έχουν τη θέση του νευρώνα. Κάθε σύνδεση έχει ένα αντίστοιχο βάρος, το οποίο σε ένα τυπικό νευρωνικό δίκτυο πολλαπλασιάζει το μεταδιδόμενο σήμα. Κάθε νευρώνας εφαρμόζει μία συνάρτηση ενεργοποίησης (συνήθως μη γραμμική) στην είσοδό του (άθροισμα των σημάτων εισόδων πολλαπλασιασμένων με τα βάρη τους) για να καθορίσει το σήμα εξόδου του.
Παρ' όλο που στις άλλες περιοχές της υπολογιστικής επιστήμης η γνώση της επιθυμητής εξόδου για δεδομένη είσοδο επιτυγχάνεται με την αποθήκευση κανόνων, στα νευρωνικά δίκτυα αυτό μπορεί να επιτευχθεί εκπαιδεύοντας το δίκτυο με ένα σύνολο παραδειγμάτων, δηλαδή ένα σύνολο δεδομένων εισόδων και αντίστοιχων εξόδων. Αυτό έχει το πλεονέκτημα ότι για να αποκτήσει το δίκτυο γνώση δε χρειάζεται να είναι γνωστοί οι μηχανισμοί επίλυσης του προβλήματος εκ των προτέρων, αλλά μπορούν να εξαχθούν αυτόματα από το νευρωνικό δίκτυο.
3.2 Μοντέλο McCulloch-Pitts
Ένα από τα πρώτα σημαντικά βήματα προς την κατεύθυνση της μελέτης των βιολογικών νευρωνικών δικτύων και της μαθηματικής μοντελοποίησής τους έγινε από τους Αμερικανούς επιστήμονες McCulloch και Pitts, οι οποίοι περιέγραψαν ένα απλό μοντέλο της δραστηριότητας του νευρώνα.
Σύμφωνα με αυτό το μοντέλο, η κατάσταση του νευρώνα περιγράφεται από ένα δυαδικό αριθμό, έστω y. Αν τότε ο νευρώνας είναι αδρανής, αν
τότε ο νευρώνας είναι αδρανής, αν 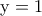 ο νευρώνας πυροδοτεί στη μέγιστη συχνότητα. Οι συνάψεις περιγράφονται από τα συναπτικά βάρη
ο νευρώνας πυροδοτεί στη μέγιστη συχνότητα. Οι συνάψεις περιγράφονται από τα συναπτικά βάρη 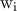 που είναι πραγματικοί αριθμοί, θετικοί για τις ενισχυτικές συνάψεις και αρνητικοί για τις ανασταλτικές συνάψεις. Αν
που είναι πραγματικοί αριθμοί, θετικοί για τις ενισχυτικές συνάψεις και αρνητικοί για τις ανασταλτικές συνάψεις. Αν  είναι οι είσοδοι του νευρώνα, τότε το άθροισμα u του φορτίου που δέχεται ο νευρώνας είναι
είναι οι είσοδοι του νευρώνα, τότε το άθροισμα u του φορτίου που δέχεται ο νευρώνας είναι

Όπως για τη δημιουργία ενός δυναμικού ενέργειας του βιολογικό νευρώνα απαιτείται η διέγερση να ξεπεράσει ένα κατώφλι δυναμικού, έτσι και στο μοντέλο McCulloch-Pitts αν το άθροισμα u είναι μεγαλύτερο από ένα κατώφλι θ τότε ο νευρώνας πυροβολεί, διαφορετικά παραμένει αδρανής. Το κατώφλι είναι ένας πραγματικός αριθμός (θετικός ή αρνητικός), όπως και τα συναπτικά βάρη . Κατ' αυτή την έννοια το κατώφλι μπορεί να θεωρηθεί ως ένα επί πλέον συναπτικό βάρος συνδεδεμένο με μια σταθερή είσοδο
. Κατ' αυτή την έννοια το κατώφλι μπορεί να θεωρηθεί ως ένα επί πλέον συναπτικό βάρος συνδεδεμένο με μια σταθερή είσοδο  η οποία έχει πάντα την τιμή -1.
η οποία έχει πάντα την τιμή -1.
Επομένως η λειτουργία του νευρώνα στο μοντέλο McCulloch-Pitts μπορεί να αναπαρασταθεί από την εξίσωση
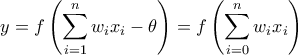
όπου f η βηματική συνάρτηση, .
.
Βηματική συνάρτηση 0/1 (step function 0/1)


Υπάρχουν πολλά διαφορετικά μοντέλα του νευρώνα που αποκλίνουν από το απλό μοντέλο McCulloch-Pitts. Η πιο σημαντική διαφορά είναι στη μορφή της μη γραμμικής συνάρτησης f(u) που χρησιμοποιείται στην έξοδο. Η συνάρτηση αυτή (που καλείται και συνάρτηση ενεργοποίησης του νευρώνα) μπορεί να πάρει εναλλακτικά τις παρακάτω μορφές:
που χρησιμοποιείται στην έξοδο. Η συνάρτηση αυτή (που καλείται και συνάρτηση ενεργοποίησης του νευρώνα) μπορεί να πάρει εναλλακτικά τις παρακάτω μορφές:
Βηματική -1/1 (step function -1/1)

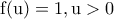
Σιγμοειδής (sigmoid)

Υπερβολική εφαπτομένη (hyperbolic tangent)


Συνάρτηση κατωφλίου (threshold function)



Συνάρτηση ράμπας (ramp function)


Γραμμική (linear)
 »
»
Προαγγελία
Στο επόμενο θα παρουσιάσουμε μια εφαρμογή των Μαθηματικών στους αγώνες δρόμου
Μοντέλο McCulloch-Pitts
Προλεγόμενα Αρκετοί συνάδελφοι μας ζήτησαν να παρουσιάσουμε κι άλλο ένα θέμα εφαρμογής των Μαθηματικών στην Ιατρική. Εμείς, μεταξύ των άλλων, διαλέξαμε άλλη μία εφαρμογή των Μαθηματικών στη νόσο του PARKINSON. Το κείμενο που ακολουθεί είναι παρμένο από τη διπλωματική εργασία της Αριστέας- Ιωάννας Γ. Φιλντίση. Η Α-Ι Φιλντίση είναι Διπλωματούχος Ηλεκτρολόγος Μηχανικός και Μηχανικός Η/Υ Ε.Μ.Π. Η διπλωματική εργασία φέρει τα παρακάτω στοιχεία:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ Η/Υ - ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ.
Θέμα: ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΔΥΝΑΤΟΤΗΤΑΣ ΠΡΟΒΛΕΨΗΣ ΤΩΝ ΝΕΥΡΩΝΙΚΩΝ ΕΚΠΟΛΩΣΕΩΝ ΑΠΟ ΤΑ ΔΥΝΑΜΙΚΑ ΤΟΠΙΚΟΥ ΠΕΔΙΟΥ.
ΧΡΗΣΗ ΜΙΚΡΟΗΛΕΚΤΡΟΔΙΑΚΩΝ ΚΑΤΑΓΡΑΦΩΝ ΑΠΟ ΤΟΝ ΥΠΟΘΑΛΑΜΙΚΟ ΠΥΡΗΝΑ ΠΑΡΚΙΝΣΟΝΙΚΩΝ ΑΣΘΕΝΩΝ ΠΟΥ ΥΠΟΒΑΛΛΟΝΤΑΙ ΣΕ ΕΝ ΤΩ ΒΑΘΕΙ ΕΓΚΕΦΑΛΙΚΗ ΔΙΕΓΕΡΣΗ
«3.1 Εισαγωγή
Ο εγκέφαλος είναι το πιο πολύπλοκο όργανο του ανθρώπινου οργανισμού. Το χαρακτηριστικό αυτό της πολυπλοκότητας τον καθιστά ικανό να εκτελεί με επιτυχία τις ανώτερες λειτουργίες που συνιστούν αυτό που αποκαλούμε νοημοσύνη. Τέτοιες λειτουργίες είναι η αναγνώριση εικόνων και φωνής, η μνήμη, η λήψη αποφάσεων, η προσαρμογή σε νέες καταστάσεις, η λογική και η μάθηση. Η τελευταία λειτουργία, δηλαδή η μάθηση, είναι ίσως ένα από τα σημαντικότερα χαρακτηριστικά του εγκεφάλου και γενικά των βιολογικών νευρωνικών δικτύων.
Η Τεχνητή Νοημοσύνη υλοποιεί τις παραπάνω λειτουργίες με την υποστήριξη ενός υλικού στρώματος. Στον άνθρωπο και τα ζώα το υλικό αυτό είναι οι νευρώνες, οι οποίοι οργανώνονται σε πυκνά δίκτυα με χιλιάδες συνάψεις ανά νευρώνα. Το αντικείμενο μελέτης της Τεχνητής Νοημοσύνης είναι αφ' ενός η ανάπτυξη ενός υλικού που θα μπορεί να υποστηρίξει τις παραπάνω λειτουργίες, ανεξάρτητα από το αν το υλικό αυτό μιμείται τους νευρώνες ή όχι, αφ' ετέρου η ανάπτυξη αλγορίθμων που θα μιμούνται αυτές τις λειτουργίες.
Ένα τεχνητό νευρωνικό δίκτυο είναι ένα σύστημα επεξεργασίας πληροφορίας που μιμείται τη δομή των βιολογικών νευρώνων και τη λειτουργία των βιολογικών νευρωνικών δικτύων. Η επεξεργασία πληροφορίας των δικτύων αυτών βασίζεται στη μετάδοση σημάτων μεταξύ απλών στοιχείων που έχουν τη θέση του νευρώνα. Κάθε σύνδεση έχει ένα αντίστοιχο βάρος, το οποίο σε ένα τυπικό νευρωνικό δίκτυο πολλαπλασιάζει το μεταδιδόμενο σήμα. Κάθε νευρώνας εφαρμόζει μία συνάρτηση ενεργοποίησης (συνήθως μη γραμμική) στην είσοδό του (άθροισμα των σημάτων εισόδων πολλαπλασιασμένων με τα βάρη τους) για να καθορίσει το σήμα εξόδου του.
Παρ' όλο που στις άλλες περιοχές της υπολογιστικής επιστήμης η γνώση της επιθυμητής εξόδου για δεδομένη είσοδο επιτυγχάνεται με την αποθήκευση κανόνων, στα νευρωνικά δίκτυα αυτό μπορεί να επιτευχθεί εκπαιδεύοντας το δίκτυο με ένα σύνολο παραδειγμάτων, δηλαδή ένα σύνολο δεδομένων εισόδων και αντίστοιχων εξόδων. Αυτό έχει το πλεονέκτημα ότι για να αποκτήσει το δίκτυο γνώση δε χρειάζεται να είναι γνωστοί οι μηχανισμοί επίλυσης του προβλήματος εκ των προτέρων, αλλά μπορούν να εξαχθούν αυτόματα από το νευρωνικό δίκτυο.
3.2 Μοντέλο McCulloch-Pitts
Ένα από τα πρώτα σημαντικά βήματα προς την κατεύθυνση της μελέτης των βιολογικών νευρωνικών δικτύων και της μαθηματικής μοντελοποίησής τους έγινε από τους Αμερικανούς επιστήμονες McCulloch και Pitts, οι οποίοι περιέγραψαν ένα απλό μοντέλο της δραστηριότητας του νευρώνα.
Σύμφωνα με αυτό το μοντέλο, η κατάσταση του νευρώνα περιγράφεται από ένα δυαδικό αριθμό, έστω y. Αν
 τότε ο νευρώνας είναι αδρανής, αν
τότε ο νευρώνας είναι αδρανής, αν 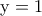 ο νευρώνας πυροδοτεί στη μέγιστη συχνότητα. Οι συνάψεις περιγράφονται από τα συναπτικά βάρη
ο νευρώνας πυροδοτεί στη μέγιστη συχνότητα. Οι συνάψεις περιγράφονται από τα συναπτικά βάρη 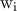 που είναι πραγματικοί αριθμοί, θετικοί για τις ενισχυτικές συνάψεις και αρνητικοί για τις ανασταλτικές συνάψεις. Αν
που είναι πραγματικοί αριθμοί, θετικοί για τις ενισχυτικές συνάψεις και αρνητικοί για τις ανασταλτικές συνάψεις. Αν  είναι οι είσοδοι του νευρώνα, τότε το άθροισμα u του φορτίου που δέχεται ο νευρώνας είναι
είναι οι είσοδοι του νευρώνα, τότε το άθροισμα u του φορτίου που δέχεται ο νευρώνας είναι
Όπως για τη δημιουργία ενός δυναμικού ενέργειας του βιολογικό νευρώνα απαιτείται η διέγερση να ξεπεράσει ένα κατώφλι δυναμικού, έτσι και στο μοντέλο McCulloch-Pitts αν το άθροισμα u είναι μεγαλύτερο από ένα κατώφλι θ τότε ο νευρώνας πυροβολεί, διαφορετικά παραμένει αδρανής. Το κατώφλι είναι ένας πραγματικός αριθμός (θετικός ή αρνητικός), όπως και τα συναπτικά βάρη
 . Κατ' αυτή την έννοια το κατώφλι μπορεί να θεωρηθεί ως ένα επί πλέον συναπτικό βάρος συνδεδεμένο με μια σταθερή είσοδο
. Κατ' αυτή την έννοια το κατώφλι μπορεί να θεωρηθεί ως ένα επί πλέον συναπτικό βάρος συνδεδεμένο με μια σταθερή είσοδο  η οποία έχει πάντα την τιμή -1.
η οποία έχει πάντα την τιμή -1.Επομένως η λειτουργία του νευρώνα στο μοντέλο McCulloch-Pitts μπορεί να αναπαρασταθεί από την εξίσωση
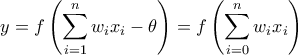
όπου f η βηματική συνάρτηση,
 .
.Βηματική συνάρτηση 0/1 (step function 0/1)


Υπάρχουν πολλά διαφορετικά μοντέλα του νευρώνα που αποκλίνουν από το απλό μοντέλο McCulloch-Pitts. Η πιο σημαντική διαφορά είναι στη μορφή της μη γραμμικής συνάρτησης f(u)
 που χρησιμοποιείται στην έξοδο. Η συνάρτηση αυτή (που καλείται και συνάρτηση ενεργοποίησης του νευρώνα) μπορεί να πάρει εναλλακτικά τις παρακάτω μορφές:
που χρησιμοποιείται στην έξοδο. Η συνάρτηση αυτή (που καλείται και συνάρτηση ενεργοποίησης του νευρώνα) μπορεί να πάρει εναλλακτικά τις παρακάτω μορφές:Βηματική -1/1 (step function -1/1)

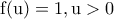
Σιγμοειδής (sigmoid)

Υπερβολική εφαπτομένη (hyperbolic tangent)


Συνάρτηση κατωφλίου (threshold function)



Συνάρτηση ράμπας (ramp function)


Γραμμική (linear)
 »
»Προαγγελία
Στο επόμενο θα παρουσιάσουμε μια εφαρμογή των Μαθηματικών στους αγώνες δρόμου
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
22ο ΣΗΜΕΙΩΜΑ
Μαθηματικά και αγώνες δρόμου
Προλεγόμενα: Πρόσφατα, ψάχνοντας για ένα θέμα, βρήκαμε μια εργασία (κοίτα "βιβλιογραφία") σχετικά με τους αγώνες δρόμου. Μας εντυπωσίασε, γιατί μελετά αυτά τα θέματα με τη βοήθεια μαθηματικών μοντέλων. Σκεφθήκαμε να το δημοσιεύσουμε αυτούσιο. Όμως το 80% των Μαθηματικών που χρησιμοποιεί είναι τελείως έξω από την περιοχή του Λυκείου, γι’ αυτό αποφασίσαμε να σας το παρουσιάσουμε προσαρμοσμένο σε επίπεδο Λυκείου. Αν τα καταφέραμε ή όχι θα μας το ’πείτε εσείς κι ο συγγραφέας του πρωτοτύπου.
Το μοντέλο J. B. Keller
Το πρόβλημα: Ο Joseph B. Keller επινόησε το 1973, ένα μαθηματικό μοντέλο για να δώσει απάντηση στο παρακάτω πρόβλημα: «με ποια ταχύτητα πρέπει να τρέξει ένας δρομέας για να καλύψει μια γνωστή απόσταση στον ελάχιστο δυνατό χρόνο;»
Οι παράμετροι: Για να απαντήσουμε στο παραπάνω πρόβλημα θα πρέπει να σημειώσουμε ότι από μόνα τους τα Μαθηματικά δεν θα πρόσφεραν πολλά πράγματα αν δεν συνδυάζονταν με τα πορίσματα και άλλων επιστημών όπως της Φυσικής, της Φυσιολογίας, της Κινησιολογίας, της Διαιτητικής κλπ. Θα πρέπει, λοιπόν, να γνωριστούμε με κάποιες έννοιες που αποτελούν "χαρακτηριστικές φυσιολογικές παραμέτρους". Να οι σημαντικότερες απ’ αυτές τις έννοιες:
Οι χαρακτηριστικές φυσιολογικές παράμετροι
 αρχική ποσότητα οξυγόνου (ενέργειας) ανά μονάδα μάζας αποθηκευμένη στους μυς του δρομέα τη στιγμή της εκκίνησης,
αρχική ποσότητα οξυγόνου (ενέργειας) ανά μονάδα μάζας αποθηκευμένη στους μυς του δρομέα τη στιγμή της εκκίνησης,  ποσότητα διαθέσιμου οξυγόνου (ενέργειας) στους μυς του δρομέα ανά μονάδα βάρους (συνάρτηση του χρόνου), σ ταχύτητα παροχής οξυγόνου (ενέργειας) ανά μονάδα μάζας μέσω του αναπνευστικού και κυκλοφοριακού συστήματος, κατά τη διάρκεια του αγωνίσματος (Φυσιολογική σταθερά που χαρακτηρίζει την ικανότητα μεταβολισμού του οξυγόνου), D το μήκος του δρόμου, Τ ο χρόνος διάνυσης της απόστασης D, t η μεταβλητή του χρόνου,
ποσότητα διαθέσιμου οξυγόνου (ενέργειας) στους μυς του δρομέα ανά μονάδα βάρους (συνάρτηση του χρόνου), σ ταχύτητα παροχής οξυγόνου (ενέργειας) ανά μονάδα μάζας μέσω του αναπνευστικού και κυκλοφοριακού συστήματος, κατά τη διάρκεια του αγωνίσματος (Φυσιολογική σταθερά που χαρακτηρίζει την ικανότητα μεταβολισμού του οξυγόνου), D το μήκος του δρόμου, Τ ο χρόνος διάνυσης της απόστασης D, t η μεταβλητή του χρόνου, 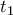 η χρονική στιγμή μετάβασης από την επιταχυνόμενη στην ομαλή κίνηση,
η χρονική στιγμή μετάβασης από την επιταχυνόμενη στην ομαλή κίνηση,  η χρονική στιγμή μετάβασης από την ομαλή στην επιβραδυνόμενη κίνηση (σημείο εξάντλησης των αποθεμάτων οξυγόνου του δρομέα),
η χρονική στιγμή μετάβασης από την ομαλή στην επιβραδυνόμενη κίνηση (σημείο εξάντλησης των αποθεμάτων οξυγόνου του δρομέα),  η βέλτιστη ταχύτητα του δρομέα,
η βέλτιστη ταχύτητα του δρομέα, 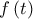 προωστική δύναμη ανά μονάδα μάζας, F: ελάχιστο άνω φράγμα (supremum) της προωστικής δύναμης ανά μονάδα μάζας (φυσιολογική σταθερά της μέγιστης δύναμης του δρομέα), τ: συντελεστής απόσβεσης (φυσιολογική σταθερά που χαρακτηρίζει την ολική αντίσταση του δρομέα). Από τις παραπάνω παραμέτρους οι σ, D, F, τ,
προωστική δύναμη ανά μονάδα μάζας, F: ελάχιστο άνω φράγμα (supremum) της προωστικής δύναμης ανά μονάδα μάζας (φυσιολογική σταθερά της μέγιστης δύναμης του δρομέα), τ: συντελεστής απόσβεσης (φυσιολογική σταθερά που χαρακτηρίζει την ολική αντίσταση του δρομέα). Από τις παραπάνω παραμέτρους οι σ, D, F, τ,  είναι "σταθερές" για κάθε δρομέα χωριστά.
είναι "σταθερές" για κάθε δρομέα χωριστά.
Η παράμετρος της ψυχολογικής κατάστασης του δρομέα δεν λαμβάνεται υπ’ όψη στο μοντέλο J. K. Keller. Θα λέγαμε πως είναι το μοντέλο για παγκόσμιους πρωταθλητές των αγώνων δρόμου.
Πρόσθετες επεξηγήσεις
Το μοντέλο J. K. Keller παρουσιάζει, επί πλέον, τα παρακάτω σημαντικά χαρακτηριστικά:
● Από φυσική άποψη στηρίζεται στο δεύτερο νόμο του Νεύτωνα. Τέλος προβλέπει δύο διαφορετικές τεχνικές: μία για δρόμους μέχρι 291m (ή κρίσιμη απόσταση) και μία για δρόμους από 291m μέχρι 10.000m
● Το μέγεθος "μάζα", επειδή μεταβάλλεται από δρομέα σε δρομέα, θα το εκφράσουμε, στις εξισώσεις που θα ακολουθήσουν, καθώς και στα μεγέθη ανά μονάδα μάζας
● Η ποιότητα οξυγόνου που είναι αποθηκευμένη
● Στους μυς είναι το μέτρο της ενέργειας που περιέχουν. Θα εκφράσουμε, λοιπόν, το διαθέσιμο οξυγόνο των μυών σε μονάδες ενέργειας (ενεργειακό ισοδύναμο του οξυγόνου). Η ενέργεια αυτή καταναλώνεται υπό μορφή κινητικής ενέργειας
● Η μεταβλητή που ελέγχει ο δρομέας είναι η προωστική του δύναμη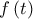 και η όλη του προσπάθεια ανάγεται στην εύρεση του βέλτιστου τρόπου μεταχείρισης της μεταβλητής αυτής για να πετύχει τον ελάχιστο χρόνο Τ.
και η όλη του προσπάθεια ανάγεται στην εύρεση του βέλτιστου τρόπου μεταχείρισης της μεταβλητής αυτής για να πετύχει τον ελάχιστο χρόνο Τ.
Επιτέλους…Μαθηματικά
Η θεωρία…: Το μοντέλο J. K. Keller χωρίζει τον αγώνα δρόμου σε τρία χρονικά διαστήματα:
i) το χρονικό διάστημα![\displaystyle{\left[ {0,t_1 }\right]} \displaystyle{\left[ {0,t_1 }\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/df99cd0646ea68a14d485f2aeb4e0ff5.png) κατά το οποίο ο δρομέας αναπτύσσει τη μεγαλύτερη δυνατή επιτάχυνση. Σ’ αυτή την περίπτωση
κατά το οποίο ο δρομέας αναπτύσσει τη μεγαλύτερη δυνατή επιτάχυνση. Σ’ αυτή την περίπτωση
 ,
, ![\displaystyle{t \in \left[ {0,t_1 } \right]} \displaystyle{t \in \left[ {0,t_1 } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/9fe774f3c309b85bf95b348bda8a9869.png)
ii) το χρονικό διάστημα [t1,t2]![\displaystyle{\left[ {t_1 ,t_2 } \right]} \displaystyle{\left[ {t_1 ,t_2 } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/8f365dda059983961c9a201d1b66536f.png)
κατά το οποίο ο δρομέας διατηρεί σταθερή ταχύτητα. Σ’ αυτή την περίπτωση βέλτιστη επιθυμητή ταχύτητα δίνεται από τον τύπο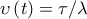 ,
, ![\displaystyle{t \in \left[ {t_1 ,t_2 } \right]} \displaystyle{t \in \left[ {t_1 ,t_2 } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/429c29b8d8c76b740fde92c7407d7165.png)
όπου λ μια παράσταση γνωστή σαν πολλαπλασιαστής του Lagrange, ο υπολογισμός της οποίας ξεφεύγει από τις δυνατότητες και τους σκοπούς του Λυκείου.
iii) το χρονικό διάστημα![\displaystyle{\left[ {t{}_2,{\rm T}} \right]} \displaystyle{\left[ {t{}_2,{\rm T}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ae894918ab4a5dd6c87e22df6d821280.png) κατά το οποίο ο δρομέας μειώνει την ταχύτητά του και από τινος και μετά τερματίζει με την κεκτημένη κινητική του ενέργεια. Σ’ αυτή την περίπτωση η βέλτιστη επιθυμητή ταχύτητα τερματισμού δίνεται από τον τύπο
κατά το οποίο ο δρομέας μειώνει την ταχύτητά του και από τινος και μετά τερματίζει με την κεκτημένη κινητική του ενέργεια. Σ’ αυτή την περίπτωση η βέλτιστη επιθυμητή ταχύτητα τερματισμού δίνεται από τον τύπο
![\displaystyle{\upsilon ^2 \left( t \right) = \sigma .\tau + \left[ {\upsilon ^2 \left( {\tau _2 } \right) - \sigma .\tau } \right]e^{\left[ {2\left( {t{}_2 - t} \right)} \right]/\tau }} \displaystyle{\upsilon ^2 \left( t \right) = \sigma .\tau + \left[ {\upsilon ^2 \left( {\tau _2 } \right) - \sigma .\tau } \right]e^{\left[ {2\left( {t{}_2 - t} \right)} \right]/\tau }}](/forum/ext/geomar/texintegr/latexrender/pictures/b2d1ca78bbd76a470d1fbb69d6fdb3fa.png) ,
, ![\displaystyle{t \in \left[ {t{}_2,{\rm T}} \right]} \displaystyle{t \in \left[ {t{}_2,{\rm T}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e163a4a3a766144f776eb25d74eda7ad.png)
...και η πράξη: Το μοντέλο J. K. Keller: α) δεν λαμβάνει υπ’ όψη του την ψυχολογική κατάσταση του δρομέα, β) οι υπολογισμοί γίνονται με βάση τις φυσιολογικές παραμέτρους των οργανισμών των παγκόσμιων πρωταθλητών και όχι του μέσου ανθρώπινου οργανισμού, γ) η διαφορά στην κατανάλωση ενέργειας από αθλητή σε αθλητή λόγω της επάνω-κάτω κίνησης του σώματος και των άκρων είναι διαφορετική, δ) η εξάντληση των αποθεμάτων οξυγόνου διαφέρει από αθλητή σε αθλητή, ε) ….
Πώς γίνεται; Η εργασία κατέληγε «Το σημείο που η θεωρία αποκλίνει από την τακτική που ακολουθούν οι δρομείς είναι ο τερματισμός. Η ταχύτητα των δρομέων παρουσιάζει μια επιτάχυνση στα τελευταία μέτρα (το γνωστό φ ί ν ι ς) σε αντίθεση με τη θεωρία που προβλέπει μια επιβράδυνση για το αντίστοιχο διάστημα. Αυτό συμβαίνει γιατί ο αντικειμενικός σκοπός του δρομέα είναι να νικήσει τους αντιπάλους του και όχι να κάνει τον ελάχιστο δυνατό χρόνο. Έτσι δεν εξαντλεί τα ενεργειακά του αποθέματα τη χρονική στιγμή t2 και τερματίζει με θετικό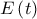 , όπου
, όπου

Αν, όμως, ακολουθούσε την τεχνική που υποδεικνύει η θεωρία θα πετύχαινε μικρότερο Τα και συνεπώς θα ήταν πιο κοντά στον αντικειμενικό σκοπό της νίκης των αντιπάλων».
Δεν είναι εντυπωσιακό;
Επιμύθιο
Από την ανάπτυξη του παραπάνω θέματος προκύπτει αβίαστα ένα σημαντικό συμπέρασμα: η ανάγκη για ερμηνεία των φαινομένων της αντικειμενικής πραγματικότητας είναι το κίνητρο για την ανάπτυξη της μαθηματικής γνώσης, η οποία με τη σειρά της μας βοηθά στην κατανόηση αυτών των φαινομένων. Άρα τα Μαθηματικά είναι ένα κλειστό σύστημα (αναπτύσσονται) και σύγχρονα ένα ανοικτό σύστημα (χρησιμοποιούνται από τις άλλες επιστήμες). Υπάρχει, δηλαδή, μια διαλεκτική σχέση ανάμεσα στα Μαθηματικά και τις άλλες επιστήμες. Η άποψη: «τα Μαθηματικά για τα Μαθηματικά» είναι, κατά τη γνώμη μας, ανεδαφική και θα λέγαμε τα αδικούν. Η όποια σχετική συζήτηση θα μας ενδιέφερε
Βιβλιογραφία
Το υλικό για να γίνει αυτή η εργασία, το δανειστήκαμε από μια εργασία του Γιώργου Δάσιου [Πανεπ. Πατρών] με θέμα «θεωρία της βέλτιστης τεχνικής για τη διεξαγωγή ενός αγώνα δρόμου». Η εργασία αυτή δημοσιεύτηκε στο περιοδικό "Μαθηματική Επιθεώρηση", τεύχ. 7, σσ. 122-142 (νέα σειρά, 197)
Μαθηματικά και αγώνες δρόμου
Προλεγόμενα: Πρόσφατα, ψάχνοντας για ένα θέμα, βρήκαμε μια εργασία (κοίτα "βιβλιογραφία") σχετικά με τους αγώνες δρόμου. Μας εντυπωσίασε, γιατί μελετά αυτά τα θέματα με τη βοήθεια μαθηματικών μοντέλων. Σκεφθήκαμε να το δημοσιεύσουμε αυτούσιο. Όμως το 80% των Μαθηματικών που χρησιμοποιεί είναι τελείως έξω από την περιοχή του Λυκείου, γι’ αυτό αποφασίσαμε να σας το παρουσιάσουμε προσαρμοσμένο σε επίπεδο Λυκείου. Αν τα καταφέραμε ή όχι θα μας το ’πείτε εσείς κι ο συγγραφέας του πρωτοτύπου.
Το μοντέλο J. B. Keller
Το πρόβλημα: Ο Joseph B. Keller επινόησε το 1973, ένα μαθηματικό μοντέλο για να δώσει απάντηση στο παρακάτω πρόβλημα: «με ποια ταχύτητα πρέπει να τρέξει ένας δρομέας για να καλύψει μια γνωστή απόσταση στον ελάχιστο δυνατό χρόνο;»
Οι παράμετροι: Για να απαντήσουμε στο παραπάνω πρόβλημα θα πρέπει να σημειώσουμε ότι από μόνα τους τα Μαθηματικά δεν θα πρόσφεραν πολλά πράγματα αν δεν συνδυάζονταν με τα πορίσματα και άλλων επιστημών όπως της Φυσικής, της Φυσιολογίας, της Κινησιολογίας, της Διαιτητικής κλπ. Θα πρέπει, λοιπόν, να γνωριστούμε με κάποιες έννοιες που αποτελούν "χαρακτηριστικές φυσιολογικές παραμέτρους". Να οι σημαντικότερες απ’ αυτές τις έννοιες:
Οι χαρακτηριστικές φυσιολογικές παράμετροι
 αρχική ποσότητα οξυγόνου (ενέργειας) ανά μονάδα μάζας αποθηκευμένη στους μυς του δρομέα τη στιγμή της εκκίνησης,
αρχική ποσότητα οξυγόνου (ενέργειας) ανά μονάδα μάζας αποθηκευμένη στους μυς του δρομέα τη στιγμή της εκκίνησης,  ποσότητα διαθέσιμου οξυγόνου (ενέργειας) στους μυς του δρομέα ανά μονάδα βάρους (συνάρτηση του χρόνου), σ ταχύτητα παροχής οξυγόνου (ενέργειας) ανά μονάδα μάζας μέσω του αναπνευστικού και κυκλοφοριακού συστήματος, κατά τη διάρκεια του αγωνίσματος (Φυσιολογική σταθερά που χαρακτηρίζει την ικανότητα μεταβολισμού του οξυγόνου), D το μήκος του δρόμου, Τ ο χρόνος διάνυσης της απόστασης D, t η μεταβλητή του χρόνου,
ποσότητα διαθέσιμου οξυγόνου (ενέργειας) στους μυς του δρομέα ανά μονάδα βάρους (συνάρτηση του χρόνου), σ ταχύτητα παροχής οξυγόνου (ενέργειας) ανά μονάδα μάζας μέσω του αναπνευστικού και κυκλοφοριακού συστήματος, κατά τη διάρκεια του αγωνίσματος (Φυσιολογική σταθερά που χαρακτηρίζει την ικανότητα μεταβολισμού του οξυγόνου), D το μήκος του δρόμου, Τ ο χρόνος διάνυσης της απόστασης D, t η μεταβλητή του χρόνου, 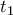 η χρονική στιγμή μετάβασης από την επιταχυνόμενη στην ομαλή κίνηση,
η χρονική στιγμή μετάβασης από την επιταχυνόμενη στην ομαλή κίνηση,  η χρονική στιγμή μετάβασης από την ομαλή στην επιβραδυνόμενη κίνηση (σημείο εξάντλησης των αποθεμάτων οξυγόνου του δρομέα),
η χρονική στιγμή μετάβασης από την ομαλή στην επιβραδυνόμενη κίνηση (σημείο εξάντλησης των αποθεμάτων οξυγόνου του δρομέα),  η βέλτιστη ταχύτητα του δρομέα,
η βέλτιστη ταχύτητα του δρομέα, 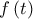 προωστική δύναμη ανά μονάδα μάζας, F: ελάχιστο άνω φράγμα (supremum) της προωστικής δύναμης ανά μονάδα μάζας (φυσιολογική σταθερά της μέγιστης δύναμης του δρομέα), τ: συντελεστής απόσβεσης (φυσιολογική σταθερά που χαρακτηρίζει την ολική αντίσταση του δρομέα). Από τις παραπάνω παραμέτρους οι σ, D, F, τ,
προωστική δύναμη ανά μονάδα μάζας, F: ελάχιστο άνω φράγμα (supremum) της προωστικής δύναμης ανά μονάδα μάζας (φυσιολογική σταθερά της μέγιστης δύναμης του δρομέα), τ: συντελεστής απόσβεσης (φυσιολογική σταθερά που χαρακτηρίζει την ολική αντίσταση του δρομέα). Από τις παραπάνω παραμέτρους οι σ, D, F, τ,  είναι "σταθερές" για κάθε δρομέα χωριστά.
είναι "σταθερές" για κάθε δρομέα χωριστά.Η παράμετρος της ψυχολογικής κατάστασης του δρομέα δεν λαμβάνεται υπ’ όψη στο μοντέλο J. K. Keller. Θα λέγαμε πως είναι το μοντέλο για παγκόσμιους πρωταθλητές των αγώνων δρόμου.
Πρόσθετες επεξηγήσεις
Το μοντέλο J. K. Keller παρουσιάζει, επί πλέον, τα παρακάτω σημαντικά χαρακτηριστικά:
● Από φυσική άποψη στηρίζεται στο δεύτερο νόμο του Νεύτωνα. Τέλος προβλέπει δύο διαφορετικές τεχνικές: μία για δρόμους μέχρι 291m (ή κρίσιμη απόσταση) και μία για δρόμους από 291m μέχρι 10.000m
● Το μέγεθος "μάζα", επειδή μεταβάλλεται από δρομέα σε δρομέα, θα το εκφράσουμε, στις εξισώσεις που θα ακολουθήσουν, καθώς και στα μεγέθη ανά μονάδα μάζας
● Η ποιότητα οξυγόνου που είναι αποθηκευμένη
● Στους μυς είναι το μέτρο της ενέργειας που περιέχουν. Θα εκφράσουμε, λοιπόν, το διαθέσιμο οξυγόνο των μυών σε μονάδες ενέργειας (ενεργειακό ισοδύναμο του οξυγόνου). Η ενέργεια αυτή καταναλώνεται υπό μορφή κινητικής ενέργειας
● Η μεταβλητή που ελέγχει ο δρομέας είναι η προωστική του δύναμη
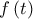 και η όλη του προσπάθεια ανάγεται στην εύρεση του βέλτιστου τρόπου μεταχείρισης της μεταβλητής αυτής για να πετύχει τον ελάχιστο χρόνο Τ.
και η όλη του προσπάθεια ανάγεται στην εύρεση του βέλτιστου τρόπου μεταχείρισης της μεταβλητής αυτής για να πετύχει τον ελάχιστο χρόνο Τ.Επιτέλους…Μαθηματικά
Η θεωρία…: Το μοντέλο J. K. Keller χωρίζει τον αγώνα δρόμου σε τρία χρονικά διαστήματα:
i) το χρονικό διάστημα
![\displaystyle{\left[ {0,t_1 }\right]} \displaystyle{\left[ {0,t_1 }\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/df99cd0646ea68a14d485f2aeb4e0ff5.png) κατά το οποίο ο δρομέας αναπτύσσει τη μεγαλύτερη δυνατή επιτάχυνση. Σ’ αυτή την περίπτωση
κατά το οποίο ο δρομέας αναπτύσσει τη μεγαλύτερη δυνατή επιτάχυνση. Σ’ αυτή την περίπτωση ,
, ![\displaystyle{t \in \left[ {0,t_1 } \right]} \displaystyle{t \in \left[ {0,t_1 } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/9fe774f3c309b85bf95b348bda8a9869.png)
ii) το χρονικό διάστημα [t1,t2]
![\displaystyle{\left[ {t_1 ,t_2 } \right]} \displaystyle{\left[ {t_1 ,t_2 } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/8f365dda059983961c9a201d1b66536f.png)
κατά το οποίο ο δρομέας διατηρεί σταθερή ταχύτητα. Σ’ αυτή την περίπτωση βέλτιστη επιθυμητή ταχύτητα δίνεται από τον τύπο
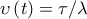 ,
, ![\displaystyle{t \in \left[ {t_1 ,t_2 } \right]} \displaystyle{t \in \left[ {t_1 ,t_2 } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/429c29b8d8c76b740fde92c7407d7165.png)
όπου λ μια παράσταση γνωστή σαν πολλαπλασιαστής του Lagrange, ο υπολογισμός της οποίας ξεφεύγει από τις δυνατότητες και τους σκοπούς του Λυκείου.
iii) το χρονικό διάστημα
![\displaystyle{\left[ {t{}_2,{\rm T}} \right]} \displaystyle{\left[ {t{}_2,{\rm T}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ae894918ab4a5dd6c87e22df6d821280.png) κατά το οποίο ο δρομέας μειώνει την ταχύτητά του και από τινος και μετά τερματίζει με την κεκτημένη κινητική του ενέργεια. Σ’ αυτή την περίπτωση η βέλτιστη επιθυμητή ταχύτητα τερματισμού δίνεται από τον τύπο
κατά το οποίο ο δρομέας μειώνει την ταχύτητά του και από τινος και μετά τερματίζει με την κεκτημένη κινητική του ενέργεια. Σ’ αυτή την περίπτωση η βέλτιστη επιθυμητή ταχύτητα τερματισμού δίνεται από τον τύπο![\displaystyle{\upsilon ^2 \left( t \right) = \sigma .\tau + \left[ {\upsilon ^2 \left( {\tau _2 } \right) - \sigma .\tau } \right]e^{\left[ {2\left( {t{}_2 - t} \right)} \right]/\tau }} \displaystyle{\upsilon ^2 \left( t \right) = \sigma .\tau + \left[ {\upsilon ^2 \left( {\tau _2 } \right) - \sigma .\tau } \right]e^{\left[ {2\left( {t{}_2 - t} \right)} \right]/\tau }}](/forum/ext/geomar/texintegr/latexrender/pictures/b2d1ca78bbd76a470d1fbb69d6fdb3fa.png) ,
, ![\displaystyle{t \in \left[ {t{}_2,{\rm T}} \right]} \displaystyle{t \in \left[ {t{}_2,{\rm T}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e163a4a3a766144f776eb25d74eda7ad.png)
...και η πράξη: Το μοντέλο J. K. Keller: α) δεν λαμβάνει υπ’ όψη του την ψυχολογική κατάσταση του δρομέα, β) οι υπολογισμοί γίνονται με βάση τις φυσιολογικές παραμέτρους των οργανισμών των παγκόσμιων πρωταθλητών και όχι του μέσου ανθρώπινου οργανισμού, γ) η διαφορά στην κατανάλωση ενέργειας από αθλητή σε αθλητή λόγω της επάνω-κάτω κίνησης του σώματος και των άκρων είναι διαφορετική, δ) η εξάντληση των αποθεμάτων οξυγόνου διαφέρει από αθλητή σε αθλητή, ε) ….
Πώς γίνεται; Η εργασία κατέληγε «Το σημείο που η θεωρία αποκλίνει από την τακτική που ακολουθούν οι δρομείς είναι ο τερματισμός. Η ταχύτητα των δρομέων παρουσιάζει μια επιτάχυνση στα τελευταία μέτρα (το γνωστό φ ί ν ι ς) σε αντίθεση με τη θεωρία που προβλέπει μια επιβράδυνση για το αντίστοιχο διάστημα. Αυτό συμβαίνει γιατί ο αντικειμενικός σκοπός του δρομέα είναι να νικήσει τους αντιπάλους του και όχι να κάνει τον ελάχιστο δυνατό χρόνο. Έτσι δεν εξαντλεί τα ενεργειακά του αποθέματα τη χρονική στιγμή t2 και τερματίζει με θετικό
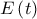 , όπου
, όπου
Αν, όμως, ακολουθούσε την τεχνική που υποδεικνύει η θεωρία θα πετύχαινε μικρότερο Τα και συνεπώς θα ήταν πιο κοντά στον αντικειμενικό σκοπό της νίκης των αντιπάλων».
Δεν είναι εντυπωσιακό;
Επιμύθιο
Από την ανάπτυξη του παραπάνω θέματος προκύπτει αβίαστα ένα σημαντικό συμπέρασμα: η ανάγκη για ερμηνεία των φαινομένων της αντικειμενικής πραγματικότητας είναι το κίνητρο για την ανάπτυξη της μαθηματικής γνώσης, η οποία με τη σειρά της μας βοηθά στην κατανόηση αυτών των φαινομένων. Άρα τα Μαθηματικά είναι ένα κλειστό σύστημα (αναπτύσσονται) και σύγχρονα ένα ανοικτό σύστημα (χρησιμοποιούνται από τις άλλες επιστήμες). Υπάρχει, δηλαδή, μια διαλεκτική σχέση ανάμεσα στα Μαθηματικά και τις άλλες επιστήμες. Η άποψη: «τα Μαθηματικά για τα Μαθηματικά» είναι, κατά τη γνώμη μας, ανεδαφική και θα λέγαμε τα αδικούν. Η όποια σχετική συζήτηση θα μας ενδιέφερε
Βιβλιογραφία
Το υλικό για να γίνει αυτή η εργασία, το δανειστήκαμε από μια εργασία του Γιώργου Δάσιου [Πανεπ. Πατρών] με θέμα «θεωρία της βέλτιστης τεχνικής για τη διεξαγωγή ενός αγώνα δρόμου». Η εργασία αυτή δημοσιεύτηκε στο περιοδικό "Μαθηματική Επιθεώρηση", τεύχ. 7, σσ. 122-142 (νέα σειρά, 197)
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
23o ΣΗΜΕΙΩΜΑ
ΜΑΘΗΜΑΤΙΚΑ ΜΟΝΤΕΛΑ ΔΙΕΘΝΩΝ
ΑΝΤΑΓΩΝΙΣΜΩΝ ΣΤΟΥΣ ΕΞΟΠΛΙΣΜΟΥΣ
Προλεγόμενα Ο Δημήτρης Χασάπης (ΕΚΠΑ), μας έχει συνηθίσει σε άρθρα με παρόμοιο περιεχόμενο. Να τι γράφει:
«Καταστάσεις φαινομένων του πραγματικού κόσμου, που οι μεταβλητές
τους αλληλοεπιδράζονται και αλληλοεπιδρούν με καθορισμένο ή τυχαίο τρόπο, ονομάζονται συνήθως "πραγματικά συστήματα" ή απλά "συστήματα"…»
Είναι γνωστό πως, από τις αρχές του δεύτερου μισού του 20ου αιώνα, καθιερώνονται τα αποκαλούμενα "μαθηματικά μοντέλα", για την κατανόηση της συμπεριφοράς των παραπάνω "συστημάτων". Όμως, πρέπει να έχουμε υπ’ όψη μας αυτό, στο οποίο ο Δημ. Χασάπης σημειώνει με έμφαση:
«Είναι ενδιαφέρον τέλος να σημειωθεί, ότι τα μαθηματικά μοντέλα των φυσικών και κοινωνικών φαινομένων και διαδικασιών, δεν είναι φιλοσοφικά και ιδεολογικά ουδέτερα , αφού στο βάθος αντικατοπτρίζουν τις αντιλήψεις του κατασκευαστή τους για τη φύση και την κοινωνία και τον τρόπο που αλληλοεξαρτώνται και αλληλοεπηρεάζονται»
ΤΟ ΜΟΝΤΕΛΟ ΤΟΥ RICHARDSON
«Το αρχικό μοντέλο, που διατύπωσε ο Richardsοn, περιγράφει την ανταγωνιστική σχέση δύο κρατών Χ,Υ που το καθένα εξοπλίζεται αντιμετωπίζοντας το ενδεχόμενο της επίθεσης του άλλου. Αν είναι η πολεμική ικανότητα ή ο συνολικός εξοπλισμός του κράτους X την χρονική στιγμή t και
είναι η πολεμική ικανότητα ή ο συνολικός εξοπλισμός του κράτους X την χρονική στιγμή t και  του κράτους Υ, τότε οι μεταβολές του
του κράτους Υ, τότε οι μεταβολές του  εξαρτιόνται απ' τις μεταβολές του
εξαρτιόνται απ' τις μεταβολές του  ) και την εχθρότητα που επικρατεί στις διαθέσεις του κράτους X απέναντι στο Υ.
) και την εχθρότητα που επικρατεί στις διαθέσεις του κράτους X απέναντι στο Υ.
Στην απλούστερη περίπτωση, παριστάνουμε τους παραπάνω όρους με k και 9 αντίστοιχα, όπου k,g είναι σταθερές "απειλής", που αισθάνεται το X και "εχθρότητας", αντίστοιχα. Ταυτόχρονα το κόστος των εξοπλισμών, που παριστάνουμε με -αχ, όπου α σταθερά "κόστους" για το κράτος X, περιορίζει τις αύξουσες μεταβολές του .
.
Μια αντίστοιχη ανάλυση για το ), οδηγεί τελικά στο σύστημα των γραμμικών διαφορικών εξισώσεων (εδώ αντίστοιχα στοιχεία των k,g είναι τα λ,h):
), οδηγεί τελικά στο σύστημα των γραμμικών διαφορικών εξισώσεων (εδώ αντίστοιχα στοιχεία των k,g είναι τα λ,h):


που αποτελούν το μαθηματικό μοντέλο του ανταγωνισμού των κρατών X και Υ στους εξοπλισμούς [όπου α,β "παράμετροι κόστους", k,λ παράμετροι "απειλής" , g,h παράμετροι "εχθρότητας", για τα κράτη Χ,Υ αντίστοιχα]
0 προσδιορισμός των παραμέτρων α,β,k,λ,g,h είναι πραγματικά ένα δύσκολο πρόβλημα και περιλαμβάνει ορισμένες αυθαίρετες υποθέσεις. Ιδιαίτερα για τον προσδιορισμό των παραμέτρων "εχθρότητας" g,h δεν υπάρχει γενικά μέθοδος, που να ανταποκρίνεται ικανοποιητικά στην πραγματικότητα. Οι παράμετροι α,β,k,λ μπορούν όμως, κατά τον Richardsοn, να προσδιοριστούν σχετικά ικανοποιητικά με βάση την ιστορική ανάλυση που εδώ παίρνει την θέση του πειράματος, που είναι η συνηθισμένη μέθοδος προσδιορισμού των παραμέτρων ενός μαθηματικού μοντέλου.
Αν το κράτος Υ έχει μηδενικό εξοπλισμό, δηλαδή y=0 και το X καμιά εχθρότητα για το Υ, δηλαδή , τότε απ' το σύστημα (1) έχουμε:
, τότε απ' το σύστημα (1) έχουμε:
ή

που σημαίνει, ότι είναι ο χρόνος, που απαιτείται για την μείωση των εξοπλισμών του κράτους X στο
είναι ο χρόνος, που απαιτείται για την μείωση των εξοπλισμών του κράτους X στο  των αρχικών εξοπλισμών.
των αρχικών εξοπλισμών.
Ο Richardsοn υποθέτει το είναι ίσο με το χρόνο μιας κοινοβουλευτικής περιόδου στο κράτος X. Για την Ελλάδα π.χ. είναι
είναι ίσο με το χρόνο μιας κοινοβουλευτικής περιόδου στο κράτος X. Για την Ελλάδα π.χ. είναι  =4 ή
=4 ή  . Το αντίστοιχο ισχύει για τον συντελεστή β του κράτους Υ.
. Το αντίστοιχο ισχύει για τον συντελεστή β του κράτους Υ.
Για τον προσδιορισμό των συντελεστών κ, λ υποθέτουμε, ότι και
και  , έτσι που
, έτσι που
Όταν τώρα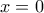 , είναι
, είναι

δηλαδή είναι ο χρόνος, που απαιτείται για να εξισωθεί ο εξοπλισμός του κράτους X με τον εξοπλισμό του Υ. Υποθέτοντας τους εξοπλισμούς του Υ σταθερούς, μπορούμε να προσδιορίσουμε το
είναι ο χρόνος, που απαιτείται για να εξισωθεί ο εξοπλισμός του κράτους X με τον εξοπλισμό του Υ. Υποθέτοντας τους εξοπλισμούς του Υ σταθερούς, μπορούμε να προσδιορίσουμε το  μe βάση τις οικονομικές και Βιομηχανικές δυνατότητες του κράτους X.
μe βάση τις οικονομικές και Βιομηχανικές δυνατότητες του κράτους X.
Για παράδειγμα ο Richardsοn χρησιμοποιεί την Γερμανία, που μετά απ' τον πλήρη αφοπλισμό της με την συνθήκη των Βερσαλλιών, επανεξοπλίστηκε και εξισώθηκε στρατιωτικά με τα γειτονικά της κράτη μέσα σε τρία χρόνια 1936-39. Οπότε για την Γερμανία του 1939, »
»
Βιβλιογραφία
Δ. Ν. Χασάπη: «Μαθηματικά Μοντέλα Διεθνών Ανταγωνισμών Στους Εξοπλισμούς», Μ.Ε. τ.17, εκδ. ΕΜΕ 1980
με εκτίμηση
Γιάννης Κερασαρίδης
ΜΑΘΗΜΑΤΙΚΑ ΜΟΝΤΕΛΑ ΔΙΕΘΝΩΝ
ΑΝΤΑΓΩΝΙΣΜΩΝ ΣΤΟΥΣ ΕΞΟΠΛΙΣΜΟΥΣ
Προλεγόμενα Ο Δημήτρης Χασάπης (ΕΚΠΑ), μας έχει συνηθίσει σε άρθρα με παρόμοιο περιεχόμενο. Να τι γράφει:
«Καταστάσεις φαινομένων του πραγματικού κόσμου, που οι μεταβλητές
τους αλληλοεπιδράζονται και αλληλοεπιδρούν με καθορισμένο ή τυχαίο τρόπο, ονομάζονται συνήθως "πραγματικά συστήματα" ή απλά "συστήματα"…»
Είναι γνωστό πως, από τις αρχές του δεύτερου μισού του 20ου αιώνα, καθιερώνονται τα αποκαλούμενα "μαθηματικά μοντέλα", για την κατανόηση της συμπεριφοράς των παραπάνω "συστημάτων". Όμως, πρέπει να έχουμε υπ’ όψη μας αυτό, στο οποίο ο Δημ. Χασάπης σημειώνει με έμφαση:
«Είναι ενδιαφέρον τέλος να σημειωθεί, ότι τα μαθηματικά μοντέλα των φυσικών και κοινωνικών φαινομένων και διαδικασιών, δεν είναι φιλοσοφικά και ιδεολογικά ουδέτερα , αφού στο βάθος αντικατοπτρίζουν τις αντιλήψεις του κατασκευαστή τους για τη φύση και την κοινωνία και τον τρόπο που αλληλοεξαρτώνται και αλληλοεπηρεάζονται»
ΤΟ ΜΟΝΤΕΛΟ ΤΟΥ RICHARDSON
«Το αρχικό μοντέλο, που διατύπωσε ο Richardsοn, περιγράφει την ανταγωνιστική σχέση δύο κρατών Χ,Υ που το καθένα εξοπλίζεται αντιμετωπίζοντας το ενδεχόμενο της επίθεσης του άλλου. Αν
 είναι η πολεμική ικανότητα ή ο συνολικός εξοπλισμός του κράτους X την χρονική στιγμή t και
είναι η πολεμική ικανότητα ή ο συνολικός εξοπλισμός του κράτους X την χρονική στιγμή t και  του κράτους Υ, τότε οι μεταβολές του
του κράτους Υ, τότε οι μεταβολές του  εξαρτιόνται απ' τις μεταβολές του
εξαρτιόνται απ' τις μεταβολές του  ) και την εχθρότητα που επικρατεί στις διαθέσεις του κράτους X απέναντι στο Υ.
) και την εχθρότητα που επικρατεί στις διαθέσεις του κράτους X απέναντι στο Υ.Στην απλούστερη περίπτωση, παριστάνουμε τους παραπάνω όρους με k και 9 αντίστοιχα, όπου k,g είναι σταθερές "απειλής", που αισθάνεται το X και "εχθρότητας", αντίστοιχα. Ταυτόχρονα το κόστος των εξοπλισμών, που παριστάνουμε με -αχ, όπου α σταθερά "κόστους" για το κράτος X, περιορίζει τις αύξουσες μεταβολές του
 .
.Μια αντίστοιχη ανάλυση για το
 ), οδηγεί τελικά στο σύστημα των γραμμικών διαφορικών εξισώσεων (εδώ αντίστοιχα στοιχεία των k,g είναι τα λ,h):
), οδηγεί τελικά στο σύστημα των γραμμικών διαφορικών εξισώσεων (εδώ αντίστοιχα στοιχεία των k,g είναι τα λ,h):
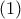

που αποτελούν το μαθηματικό μοντέλο του ανταγωνισμού των κρατών X και Υ στους εξοπλισμούς [όπου α,β "παράμετροι κόστους", k,λ παράμετροι "απειλής" , g,h παράμετροι "εχθρότητας", για τα κράτη Χ,Υ αντίστοιχα]
0 προσδιορισμός των παραμέτρων α,β,k,λ,g,h είναι πραγματικά ένα δύσκολο πρόβλημα και περιλαμβάνει ορισμένες αυθαίρετες υποθέσεις. Ιδιαίτερα για τον προσδιορισμό των παραμέτρων "εχθρότητας" g,h δεν υπάρχει γενικά μέθοδος, που να ανταποκρίνεται ικανοποιητικά στην πραγματικότητα. Οι παράμετροι α,β,k,λ μπορούν όμως, κατά τον Richardsοn, να προσδιοριστούν σχετικά ικανοποιητικά με βάση την ιστορική ανάλυση που εδώ παίρνει την θέση του πειράματος, που είναι η συνηθισμένη μέθοδος προσδιορισμού των παραμέτρων ενός μαθηματικού μοντέλου.
Αν το κράτος Υ έχει μηδενικό εξοπλισμό, δηλαδή y=0 και το X καμιά εχθρότητα για το Υ, δηλαδή
 , τότε απ' το σύστημα (1) έχουμε:
, τότε απ' το σύστημα (1) έχουμε: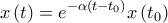
ή

που σημαίνει, ότι
 είναι ο χρόνος, που απαιτείται για την μείωση των εξοπλισμών του κράτους X στο
είναι ο χρόνος, που απαιτείται για την μείωση των εξοπλισμών του κράτους X στο  των αρχικών εξοπλισμών.
των αρχικών εξοπλισμών.Ο Richardsοn υποθέτει το
 είναι ίσο με το χρόνο μιας κοινοβουλευτικής περιόδου στο κράτος X. Για την Ελλάδα π.χ. είναι
είναι ίσο με το χρόνο μιας κοινοβουλευτικής περιόδου στο κράτος X. Για την Ελλάδα π.χ. είναι  =4 ή
=4 ή 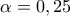 . Το αντίστοιχο ισχύει για τον συντελεστή β του κράτους Υ.
. Το αντίστοιχο ισχύει για τον συντελεστή β του κράτους Υ.Για τον προσδιορισμό των συντελεστών κ, λ υποθέτουμε, ότι
 και
και  , έτσι που
, έτσι που 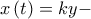
Όταν τώρα
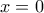 , είναι
, είναι
δηλαδή
 είναι ο χρόνος, που απαιτείται για να εξισωθεί ο εξοπλισμός του κράτους X με τον εξοπλισμό του Υ. Υποθέτοντας τους εξοπλισμούς του Υ σταθερούς, μπορούμε να προσδιορίσουμε το
είναι ο χρόνος, που απαιτείται για να εξισωθεί ο εξοπλισμός του κράτους X με τον εξοπλισμό του Υ. Υποθέτοντας τους εξοπλισμούς του Υ σταθερούς, μπορούμε να προσδιορίσουμε το  μe βάση τις οικονομικές και Βιομηχανικές δυνατότητες του κράτους X.
μe βάση τις οικονομικές και Βιομηχανικές δυνατότητες του κράτους X.Για παράδειγμα ο Richardsοn χρησιμοποιεί την Γερμανία, που μετά απ' τον πλήρη αφοπλισμό της με την συνθήκη των Βερσαλλιών, επανεξοπλίστηκε και εξισώθηκε στρατιωτικά με τα γειτονικά της κράτη μέσα σε τρία χρόνια 1936-39. Οπότε για την Γερμανία του 1939,
 »
»Βιβλιογραφία
Δ. Ν. Χασάπη: «Μαθηματικά Μοντέλα Διεθνών Ανταγωνισμών Στους Εξοπλισμούς», Μ.Ε. τ.17, εκδ. ΕΜΕ 1980
με εκτίμηση
Γιάννης Κερασαρίδης
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
24ο ΣΗΜΕΙΩΜΑ
ΠΡΟΒΛΗΜΑ ΥΠΟΒΡΥΧΙΟΥ ΠΟΛΕΜΟΥ
Προλεγόμενα Μια και στο προηγούμενο σημείωμα μιλούσαμε για τον ανταγωνισμό στους διεθνείς εξοπλισμούς, θυμηθήκαμε πως είχαμε διαβάσει, παλιά, μια εργασία του Δ. Γ. Μάγειρα, σχετική μ’ αυτά. Ψάξαμε, τη βρήκαμε και σας παρουσιάζουμε ένα ελάχιστο κομμάτι της, που αναφέρεται στη συμβολή της επιστήμης των Μαθηματικών, στην επίλυση προβλημάτων που ανέκυπταν στον αγώνα των συμμάχων κατά τον Β΄ Παγκόσμιο Πόλεμο. Πρέπει να σημειώσουμε δύο πράγματα: α) το "πρόβλημα των θόλων" αποτελεί μια πολύ δύσκολη περίπτωση κατασκευής μαθηματικού μοντέλου και β) χρησιμοποιεί πολύ εξειδικευμένα Μαθηματικά. Εξ αιτίας αυτών επιλέξαμε μέρη και τα "συρράψαμε" με ό,τι αυτό μπορεί να συνεπάγεται.
ΤΟ ΠΡΟΒΛΗΜΑ ΤΩΝ "ΘΟΛΩΝ"
«Το "πρόβλημα των θόλων" προέκυψε το 1942-1943 σε σχέση με τον τότε υποβρύχιο πόλεμο, αποτελεί δε αξιόλογο παράδειγμα με το οποίο δείχνεται η δυσκολία κατασκευής μαθηματικών μοντέλων για πρακτικούς σκοπούς άμεσης ανάγκης.
Όταν από μια πλάκα, η οποία βρίσκεται μέσα σε ταχέως κινούμενο υποβρύχιο, στέλλει προς τα έξω δέσμη ηχητικών ακτίνων τότε, λέμε, ότι έχουμε μια "υποβρύχια ηχητική βολή".
Κατά την υποβρύχια ηχητική βολή, οι ατμοί νερού που εκπέμπονται από τα πέριξ της πλάκας, προκαλούν διαταραχές, και, προς εξάλειψή τους, η πλάκα τίθεται μέσα σε κοίλο κέλυφος πλήρες νερού. Αυτή η ηχητική συσκευή λέγεται "θόλος".
Κατά το 1942-1943 οι πολεμικές ανάγκες επέβαλαν να κατασκευαστεί μεγάλος αριθμός από μικρά καταδιωκτικά υποβρύχια εφοδιασμένα με μικρούς θόλους. Όταν γινόταν η κατασκευή των θόλων αυτών, παρατηρήθηκε ότι αυτοί προκαλούσαν μια μη ανεκτή διάχυση και αραίωση του ακτινοβολούμενου ήχου, κρίθηκε δε σαν επιτακτική ανάγκη η διόρθωση του κακού. Τότε η μαθηματική ανάλυση του προβλήματος, συνοδευόμενη από ταχύ πειραματικό έργο, έδωσε την αναμενόμενη λύση εις το επείγον τότε αυτό πρόβλημα…»
«…Το μοντέλο, όμως, αυτό αποδείχθηκε ως ακατάλληλο για το πρόβλημα και καταβλήθηκε προσπάθεια με σκοπό, αυτό, να τροποποιηθεί κατάλληλα. Ο μικρός θόλος μικρού πάχους αντικαταστάθηκε από άλλο θόλο πολύ μικρότερου πάχους, οπότε η επίδραση του θόλου αντικαταστάθηκε από άλλες συνθήκες "πηδημάτων ασυνέχειας" (Jump discontinuities), της διαταραχής q της ηχητικής δέσμης δια μέσου της επιφανείας του θόλου….»
«…Αυτές οι συνθήκες ("πηδημάτων ασυνέχειας") γράφονται με τη μορφή
![\displaystyle{\left[ q \right] = \frac{{p_1 }}{{p_0^{ - 1} }}\frac{{\partial p}}{{\partial x}}} \displaystyle{\left[ q \right] = \frac{{p_1 }}{{p_0^{ - 1} }}\frac{{\partial p}}{{\partial x}}}](/forum/ext/geomar/texintegr/latexrender/pictures/7dfe031e2d7d4399f4a13f38cf5d9d2f.png)
και
![\displaystyle{\left[ {\frac{{\partial q}}{{\partial n}}} \right] = \frac{{p_0 }}{p}\left( {{\rm K}_0^2 - {\rm K}_1^2 } \right)p - \left( {1 - \frac{{p_0 }}{p}} \right)\left( {\frac{{\partial ^2 p}}{{\partial n^2 }} - 2H\frac{{\partial p}}{{\partial n}}} \right)} \displaystyle{\left[ {\frac{{\partial q}}{{\partial n}}} \right] = \frac{{p_0 }}{p}\left( {{\rm K}_0^2 - {\rm K}_1^2 } \right)p - \left( {1 - \frac{{p_0 }}{p}} \right)\left( {\frac{{\partial ^2 p}}{{\partial n^2 }} - 2H\frac{{\partial p}}{{\partial n}}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/819c21e89a3f838a84b5fb41e2a266ba.png)
όπου:
•![\displaystyle{\left[ { } \right]} \displaystyle{\left[ { } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/79def4d77cf7f96ac15be22327aa2b36.png) σημαίνει πήδημα της υπό το σύμβολο ποσότητας δια μέσου της επιφανείας,
σημαίνει πήδημα της υπό το σύμβολο ποσότητας δια μέσου της επιφανείας,
• q είναι η διαταραχή της ακουστικής πίεσης p που προκαλείται από το θόλο,
• είναι "ορθογώνια παράγωγος" (normal derivative), η οποία πρέπει να υπολογισθεί πάνω στην επιφάνεια S του θόλου,
είναι "ορθογώνια παράγωγος" (normal derivative), η οποία πρέπει να υπολογισθεί πάνω στην επιφάνεια S του θόλου,
• Η είναι η μέση καμπυλότητα της επιφάνειας S, δηλ. ο μέσος όρος των καμπυλοτήτων μεταξύ δύο καθέτων διατομών
• Τα q,s πρέπει να επαληθεύουν τις παραπάνω συνθήκες»
«…Το πρόβλημα αυτό έχει μοναδική λύση την:
![\displaystyle{q = - \frac{1}{{4\pi }}\int\limits_s {\int {\left[ {\frac{{\partial q}}{{\partial n}}} \right]} } \frac{{e^{ik_0 r} }}{{r}}ds + \frac{1}{{4\pi }}\int\limits_s {\int {\left[ q \right]} } \frac{\partial }{{\partial x}}\left( {\frac{{e^{ikr} }}{{r}}} \right)ds} \displaystyle{q = - \frac{1}{{4\pi }}\int\limits_s {\int {\left[ {\frac{{\partial q}}{{\partial n}}} \right]} } \frac{{e^{ik_0 r} }}{{r}}ds + \frac{1}{{4\pi }}\int\limits_s {\int {\left[ q \right]} } \frac{\partial }{{\partial x}}\left( {\frac{{e^{ikr} }}{{r}}} \right)ds}](/forum/ext/geomar/texintegr/latexrender/pictures/bb806255bf7c537a254a9590d965c6d5.png) ,
,
…..»
ΠΡΟΒΛΗΜΑ ΥΠΟΒΡΥΧΙΟΥ ΠΟΛΕΜΟΥ
Προλεγόμενα Μια και στο προηγούμενο σημείωμα μιλούσαμε για τον ανταγωνισμό στους διεθνείς εξοπλισμούς, θυμηθήκαμε πως είχαμε διαβάσει, παλιά, μια εργασία του Δ. Γ. Μάγειρα, σχετική μ’ αυτά. Ψάξαμε, τη βρήκαμε και σας παρουσιάζουμε ένα ελάχιστο κομμάτι της, που αναφέρεται στη συμβολή της επιστήμης των Μαθηματικών, στην επίλυση προβλημάτων που ανέκυπταν στον αγώνα των συμμάχων κατά τον Β΄ Παγκόσμιο Πόλεμο. Πρέπει να σημειώσουμε δύο πράγματα: α) το "πρόβλημα των θόλων" αποτελεί μια πολύ δύσκολη περίπτωση κατασκευής μαθηματικού μοντέλου και β) χρησιμοποιεί πολύ εξειδικευμένα Μαθηματικά. Εξ αιτίας αυτών επιλέξαμε μέρη και τα "συρράψαμε" με ό,τι αυτό μπορεί να συνεπάγεται.
ΤΟ ΠΡΟΒΛΗΜΑ ΤΩΝ "ΘΟΛΩΝ"
«Το "πρόβλημα των θόλων" προέκυψε το 1942-1943 σε σχέση με τον τότε υποβρύχιο πόλεμο, αποτελεί δε αξιόλογο παράδειγμα με το οποίο δείχνεται η δυσκολία κατασκευής μαθηματικών μοντέλων για πρακτικούς σκοπούς άμεσης ανάγκης.
Όταν από μια πλάκα, η οποία βρίσκεται μέσα σε ταχέως κινούμενο υποβρύχιο, στέλλει προς τα έξω δέσμη ηχητικών ακτίνων τότε, λέμε, ότι έχουμε μια "υποβρύχια ηχητική βολή".
Κατά την υποβρύχια ηχητική βολή, οι ατμοί νερού που εκπέμπονται από τα πέριξ της πλάκας, προκαλούν διαταραχές, και, προς εξάλειψή τους, η πλάκα τίθεται μέσα σε κοίλο κέλυφος πλήρες νερού. Αυτή η ηχητική συσκευή λέγεται "θόλος".
Κατά το 1942-1943 οι πολεμικές ανάγκες επέβαλαν να κατασκευαστεί μεγάλος αριθμός από μικρά καταδιωκτικά υποβρύχια εφοδιασμένα με μικρούς θόλους. Όταν γινόταν η κατασκευή των θόλων αυτών, παρατηρήθηκε ότι αυτοί προκαλούσαν μια μη ανεκτή διάχυση και αραίωση του ακτινοβολούμενου ήχου, κρίθηκε δε σαν επιτακτική ανάγκη η διόρθωση του κακού. Τότε η μαθηματική ανάλυση του προβλήματος, συνοδευόμενη από ταχύ πειραματικό έργο, έδωσε την αναμενόμενη λύση εις το επείγον τότε αυτό πρόβλημα…»
«…Το μοντέλο, όμως, αυτό αποδείχθηκε ως ακατάλληλο για το πρόβλημα και καταβλήθηκε προσπάθεια με σκοπό, αυτό, να τροποποιηθεί κατάλληλα. Ο μικρός θόλος μικρού πάχους αντικαταστάθηκε από άλλο θόλο πολύ μικρότερου πάχους, οπότε η επίδραση του θόλου αντικαταστάθηκε από άλλες συνθήκες "πηδημάτων ασυνέχειας" (Jump discontinuities), της διαταραχής q της ηχητικής δέσμης δια μέσου της επιφανείας του θόλου….»
«…Αυτές οι συνθήκες ("πηδημάτων ασυνέχειας") γράφονται με τη μορφή
![\displaystyle{\left[ q \right] = \frac{{p_1 }}{{p_0^{ - 1} }}\frac{{\partial p}}{{\partial x}}} \displaystyle{\left[ q \right] = \frac{{p_1 }}{{p_0^{ - 1} }}\frac{{\partial p}}{{\partial x}}}](/forum/ext/geomar/texintegr/latexrender/pictures/7dfe031e2d7d4399f4a13f38cf5d9d2f.png)
και
![\displaystyle{\left[ {\frac{{\partial q}}{{\partial n}}} \right] = \frac{{p_0 }}{p}\left( {{\rm K}_0^2 - {\rm K}_1^2 } \right)p - \left( {1 - \frac{{p_0 }}{p}} \right)\left( {\frac{{\partial ^2 p}}{{\partial n^2 }} - 2H\frac{{\partial p}}{{\partial n}}} \right)} \displaystyle{\left[ {\frac{{\partial q}}{{\partial n}}} \right] = \frac{{p_0 }}{p}\left( {{\rm K}_0^2 - {\rm K}_1^2 } \right)p - \left( {1 - \frac{{p_0 }}{p}} \right)\left( {\frac{{\partial ^2 p}}{{\partial n^2 }} - 2H\frac{{\partial p}}{{\partial n}}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/819c21e89a3f838a84b5fb41e2a266ba.png)
όπου:
•
![\displaystyle{\left[ { } \right]} \displaystyle{\left[ { } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/79def4d77cf7f96ac15be22327aa2b36.png) σημαίνει πήδημα της υπό το σύμβολο ποσότητας δια μέσου της επιφανείας,
σημαίνει πήδημα της υπό το σύμβολο ποσότητας δια μέσου της επιφανείας, • q είναι η διαταραχή της ακουστικής πίεσης p που προκαλείται από το θόλο,
•
 είναι "ορθογώνια παράγωγος" (normal derivative), η οποία πρέπει να υπολογισθεί πάνω στην επιφάνεια S του θόλου,
είναι "ορθογώνια παράγωγος" (normal derivative), η οποία πρέπει να υπολογισθεί πάνω στην επιφάνεια S του θόλου, • Η είναι η μέση καμπυλότητα της επιφάνειας S, δηλ. ο μέσος όρος των καμπυλοτήτων μεταξύ δύο καθέτων διατομών
• Τα q,s πρέπει να επαληθεύουν τις παραπάνω συνθήκες»
«…Το πρόβλημα αυτό έχει μοναδική λύση την:
![\displaystyle{q = - \frac{1}{{4\pi }}\int\limits_s {\int {\left[ {\frac{{\partial q}}{{\partial n}}} \right]} } \frac{{e^{ik_0 r} }}{{r}}ds + \frac{1}{{4\pi }}\int\limits_s {\int {\left[ q \right]} } \frac{\partial }{{\partial x}}\left( {\frac{{e^{ikr} }}{{r}}} \right)ds} \displaystyle{q = - \frac{1}{{4\pi }}\int\limits_s {\int {\left[ {\frac{{\partial q}}{{\partial n}}} \right]} } \frac{{e^{ik_0 r} }}{{r}}ds + \frac{1}{{4\pi }}\int\limits_s {\int {\left[ q \right]} } \frac{\partial }{{\partial x}}\left( {\frac{{e^{ikr} }}{{r}}} \right)ds}](/forum/ext/geomar/texintegr/latexrender/pictures/bb806255bf7c537a254a9590d965c6d5.png) ,
,…..»
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
Προλεγόμενα
Πολύς λόγος γίνεται τελευταία για τα χρηματοοικονομικά τερτίπια της διεθνούς τοκογλυφίας. Αναφερόμαστε, προφανώς, στα "χρηματοοικονομικά παράγωγα". Η εργασία που ακολουθεί αναφέρεται στο ευρωπαϊκό χρηματοοικονομικό δικαίωμα και συναφή θέματα:
25ο ΣΗΜΕΙΩΜΑ
"ΕΝΑ ΜΟΝΤΕΛΟ ΤΗΣ ΑΝΑΜΕΝΟΜΕΝΗΣ ΑΡΧΙΚΗΣ ΑΞΙΑΣ ΤΟΥ ΕΥΡΩΠΑΪΚΟΥ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΟΥ ΔΙΚΑΙΩΜΑΤΟΣ"[/i][/color][/b]
ΑΝΑΣΤΑΣΙΟΥ ΣΟΥΠΑΝΝΗ ΑΘΑΝΑΣΙΟΥ ΜΠΕΛΛΑ
ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΙΡΑΙΩΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΑΣ
1. Εισαγωγή
Τα παράγωγα χρηματοοικονομικά εργαλεία [derivactive financial instruments] είναι χρηματοοικονομικά εργαλεία με τα οποία μπορεί κάποιος να κερδίσει ή να χάσει χρήματα προβλέποντας τις μεταβολές που θα έχουν οι τιμές διαφόρων αξιόγραφων ή προϊόντων. Τα παράγωγα αναπτύχτηκαν και χρησιμοποιούνται ως ένας τρόπος προστασίας των επιχειρήσεων και των επενδυτών από τις απότομες μεταβολές των τιμών στις αγορές συναλλάγματος, επιτοκίων, μετάλλων, και πρώτων υλών. Μια εισαγωγική επιχείρηση που πρόκειται να πληρώσει τις υποχρεώσεις της σε συνάλλαγμα μπορεί να κάνει χρήση ενός παράγωγου για να προφυλαχθεί από μια υποτίμηση συμφωνώντας να αγοράσει συνάλλαγμα την ημέρα της πληρωμής σε προκαθορισμένη τιμή. Η ανάπτυξη των παραγώγων υπήρξε πολύ γρήγορη διότι μετά την κατάργηση της συμφωνίας του Breton Woods και την ελεύθερη διακύμανση των συναλλαγματικών ισοτιμιών, οι χρηματοοικονομικές αγορές έγιναν πολύ ασταθείς. Η ανάγκη προστασίας από τους συναλλαγματικούς κινδύνους συνέβαλε στη γρήγορη ανάπτυξη των παραγωγών σε ομόλογα, νομίσματα ή μετοχές μετά τα μέσα της προηγούμενης δεκαετίας. Ένα σημαντικό πρόβλημα που αντιμετωπίζουν οι κεντρικές τράπεζες και οι κυβερνήσεις είναι ο τρόπος με τον οποίο οι μεγάλες διεθνείς τράπεζες χρησιμοποιούν τα παράγωγα, οι οποίες δεν διστάζουν να αναλάβουν μεγάλους κερδοσκοπικούς κινδύνους διαθέτοντας τεράστια ποσά στα παράγωγα εκμεταλλευόμενες το μικρό κόστος των εργαλείων αυτών[1].
Σύμφωνα με τα ευρήματα εμπειρικών μελετών στις πράξεις των παραγώγων υπεισέρχονται παράγοντες, οι οποίοι δημιουργούν προβλήματα στη Διοίκηση Κινδύνου [Risk Management], όπως:
Περιορισμένη εμπειρία των συμμετεχόντων - Περιπλοκότητα των πράξεων των παραγώγων - Ελκυστικότητα του βραχυχρόνιου κέρδους - Παραγνώριση των κινδύνων λόγω βραχυχρόνιου κέρδους. Επειδή στις πράξεις των παραγώγων οι συμμετέχοντες δεν έχουν την δυνατότητα ή δεν θέλουν να ανακαλύψουν τους κινδύνους τότε θεωρείται απαραίτητη η λήψη ορισμένων μέτρων, όπως:
— Δημιουργία νέου νομοθετικού αυστηρού πλαισίου που θα θεσμοθετεί τους κανόνες λειτουργίας των πράξεων των παραγώγων.
— Διεξαγωγή των πράξεων των παραγώγων μόνο από τράπεζες με υποχρέωση ανακοίνωσης των πράξεων αυτών στη κεντρική τράπεζα με σύγχρονη αλλαγή στον τρόπο λογιστικοποίησης αυτών
— Καλύτερη οργάνωση των τραπεζών στον τομέα της Διοίκησης Κινδύνου και εκπαίδευση του προσωπικού στον τομέα των παραγώγων.
— Ανάπτυξη νέων μεθόδων στις διαδικασίες λήψης αποφάσεων σχετικά με τα παράγωγα, δηλαδή κατασκευή μοντέλων που θα δίνουν τη δυνατότητα ευκολότερης και καλύτερης ποσοτικής ανάλυσης των κινδύνων [ 4 ].
Σκοπός της εργασίας αυτής είναι να παρουσιάσει ένα μοντέλο για τη λήψη αποφάσεων σχετικά με το Ευρωπαϊκό χρηματοοικονομικό δικαίωμα το οποίο είναι ένα παράγωγο χρηματοοικονομικό εργαλείο.
2. Χρηματοοικονομικό Δικαίωμα
Το χρηματοοικονομικό δικαίωμα [option] είναι ένα χρηματοοικονομικό εργαλείο το οποίο δίνει στον κάτοχό του το δικαίωμα, χωρίς υποχρέωση , αγοράς ή πώλησης ενός αξιόγραφου ή προϊόντος σε μια μελλοντική χρονική στιγμή και σε μια προκαθορισμένη τιμή η οποία λέγεται τιμή άσκησης δικαιώματος. Το δικαίωμα αυτό ισχύει για ένα χρονικό διάστημα που ορίζεται κατά την αγορά του χρηματοοικονομικού δικαιώματος. Το τέλος του χρονικού αυτού διαστήματος λέγεται λήξη του χρηματοοικονομικού δικαιώματος. Υπάρχουν δυο τύποι χρηματοοικονομικών δικαιωμάτων : Το χρηματοοικονομικό δικαίωμα αγοράς το οποίο δίνει στον κάτοχο του το δικαίωμα αγοράς ενός αξιόγραφου ή προϊόντος στην προκαθορισμένη τιμή και το χρηματοοικονομικό δικαίωμα πώλησης το οποίο δίνει στον κάτοχό του το δικαίωμα πώλησης ενός αξιόγραφου ή προϊόντος στην προκαθορισμένη τιμή, είναι προφανές ότι στην λήξη ενός χρηματοοικονομικού δικαιώματος, ο κάτοχός του έχει την δυνατότητα να χρησιμοποιήσει το "δικαίωμα" , δηλαδή να αγοράσει ή να πουλήσει το αξιόγραφο ή το αγαθό, μόνο αν η τιμή είναι συμφέρουσα γι αυτόν.
Στην αντίθετη περίπτωση δεν το κάνει και το χρηματοοικονομικό δικαίωμα λήγει. Σύμφωνα με το Ευρωπαϊκό χρηματοοικονομικό δικαίωμα η άσκηση του δικαιώματος πώλησης ή αγοράς γίνεται κατά τη Λήξη του χρηματοοικονομικού δικαιώματος. Σύμφωνα όμως με το Αμερικάνικο χρηματοοικονομικό δικαίωμα η άσκηση του δικαιώματος αγοράς ή πώλησης μπορεί να γίνει σε οποιαδήποτε χρονική στιγμή του χρονικού διαστήματος που ορίζεται από τη χρονική στιγμή αγοράς και τη χρονική στιγμή λήξης του χρηματοοικονομικού δικαιώματος [2].
Σκοπός της εργασίας αυτής είναι να παρουσιάσει με κάθε δυνατή λεπτομέρεια ένα μοντέλο υπολογισμού της αναμενόμενης αρχικής αξίας του Ευρωπαϊκού χρηματοοικονομικού δικαιώματος [3].
3. Υποθέσεις του Μοντέλου
Σκοπός του τρίτου μέρους της εργασίας είναι, να παρουσιάσει τις υποθέσεις στις οποίες βασίζεται το μοντέλο που αναπτύσσεται στο τέταρτο μέρος της εργασίας.
Το χρονικό διάστημα [που ορίζεται από τη χρονική στιγμή αγοράς και τη χρονική στιγμή της λήξης του χρηματοοικονομικού δικαιώματος χωρίζεται σε η ίσες χρονικές περιόδους. Το επιτόκιο κάθε χρονικής περιόδου είναι i και η τιμή αγοράς του αξιόγραφου κατά την χρονική στιγμή είναι 0 είναι S. Κατά τη διάρκεια μιας χρονικής περιόδου η τιμή του αξιόγραφου αυξάνεται με πιθανότητα p ή μειώνεται με πιθανότητα .
.
Αύξηση της τιμής του αξιόγραφου κατά τη διάρκεια μιας χρονικής περιόδου σημαίνει ότι η τιμή του αξιόγραφου στο τέλος της χρονικής περιόδου είναι το αποτέλεσμα του πολλαπλασιασμού της τιμής του αξιόγραφου στην αρχή της χρονικής περιόδου με τον παράγοντα , όπου
, όπου 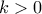 . Μείωση της τιμής του αξιόγραφου κατά τη διάρκεια μιας χρονικής περιόδου σημαίνει ότι η τιμή του αξιόγραφου στο τέλος της χρονικής περιόδου είναι το αποτέλεσμα του πολλαπλασιασμού της τιμής του αξιόγραφου στην αρχή της περιόδου με τον παράγοντα
. Μείωση της τιμής του αξιόγραφου κατά τη διάρκεια μιας χρονικής περιόδου σημαίνει ότι η τιμή του αξιόγραφου στο τέλος της χρονικής περιόδου είναι το αποτέλεσμα του πολλαπλασιασμού της τιμής του αξιόγραφου στην αρχή της περιόδου με τον παράγοντα  ,
, 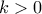
Η αύξηση ή η μείωση της τιμής του αξιόγραφου σε μια χρονική περίοδο είναι ανεξάρτητη από την αύξηση ή μείωση της τιμής του αξιόγραφου σε κάθε άλλη χρονική περίοδο.
4. Ανάπτυξη του Μοντέλου
Έστω Τ τυχαία μεταβλητή η οποία παριστάνει τον αριθμό των χρονικών περιόδων στις οποίες μειώθηκε η τιμή του αξιόγραφου. Η τυχαία μεταβλητή Τ παίρνει τις τιμές 0,1,…, η.
Η πιθανότητα αύξησης της τιμής του αξιόγραφου σε κάποια χρονική περίοδο είναι p και είναι η πιθανότητα μείωσης της τιμής του αξιόγραφου στην ίδια χρονική περίοδο. Επειδή η μείωση ή η αύξηση της τιμής του αξιόγραφου σε κάποια χρονική περίοδο είναι ανεξάρτητη από τη μείωση ή αύξηση της τιμής του αξιόγραφου σε κάθε άλλη χρονική περίοδο τότε η τυχαία μεταβλητή Τ ακολουθεί τη διωνυμική κατανομή [ 6 ].
είναι η πιθανότητα μείωσης της τιμής του αξιόγραφου στην ίδια χρονική περίοδο. Επειδή η μείωση ή η αύξηση της τιμής του αξιόγραφου σε κάποια χρονική περίοδο είναι ανεξάρτητη από τη μείωση ή αύξηση της τιμής του αξιόγραφου σε κάθε άλλη χρονική περίοδο τότε η τυχαία μεταβλητή Τ ακολουθεί τη διωνυμική κατανομή [ 6 ].
Η συνάρτηση πιθανότητας της τυχαίας μεταβλητής Τ είναι :
![\displaystyle{P\left[ {T = t} \right] = \left( \begin{array}{l}n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} } \displaystyle{P\left[ {T = t} \right] = \left( \begin{array}{l}n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} }](/forum/ext/geomar/texintegr/latexrender/pictures/a9361565f3362d8dbb30fcf3f173f25b.png) ,
, 
Υποθέτουμε ότι τότε η τιμή του αξιόγραφου κατά τη χρονική στιγμή n, η οποία είναι η στιγμή λήξης του χρηματοοικονομικού δικαιώματος, είναι
τότε η τιμή του αξιόγραφου κατά τη χρονική στιγμή n, η οποία είναι η στιγμή λήξης του χρηματοοικονομικού δικαιώματος, είναι
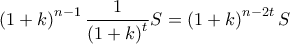
διότι η τιμή του αξιόγραφου αυξήθηκε σε χρονικές περιόδους και μειώθηκε σε i χρονικές περιόδους [ 5 ]. Συμβολίζουμε με Ε την τιμή άσκησης του δικαιώματος. Αν
χρονικές περιόδους και μειώθηκε σε i χρονικές περιόδους [ 5 ]. Συμβολίζουμε με Ε την τιμή άσκησης του δικαιώματος. Αν
 ,
, 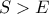
τότε η αξία του αξιόγραφου κατά την χρονική στιγμή η είναι:

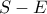
Αν

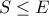
τότε η αξία του αξιόγραφου κατά την χρονική στιγμή η είναι 0. Επομένως η αξία του αξιόγραφου κατά την χρονική στιγμή η είναι:
![\displaystyle{\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \displaystyle{\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/b2bdbc7123863a940e02b84e85742951.png)
και
![\displaystyle{\frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1+k} \right)^{n - 2t} S - E} \right]} \displaystyle{\frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1+k} \right)^{n - 2t} S - E} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/1d838c2df6d737149c30e94d74e8ea9e.png)
είναι η αρχική αξία του αξιόγραφου κατά την χρονική στιγμή 0 όταν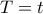 .
.
Έστω V τυχαία μεταβλητή η οποία παριστάνει την αρχική αξία του αξιόγραφου κατά την χρονική στιγμή 0. Το ενδεχόμενο
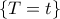 , συνεπάγεται το ενδεχόμενο
, συνεπάγεται το ενδεχόμενο
![\displaystyle{\left\{ {V = \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \right\}} \displaystyle{\left\{ {V = \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \right\}}](/forum/ext/geomar/texintegr/latexrender/pictures/bf5d16119bbeceb62f4a1827f9a8879e.png)
και αντίστροφα. Επομένως από την (4.1) έχουμε:
![\displaystyle{P\left\{ {V = \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \right\} = P\left[ {T = t} \right] = \[\left( \begin{array}{l} n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} } \displaystyle{P\left\{ {V = \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \right\} = P\left[ {T = t} \right] = \[\left( \begin{array}{l} n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} }](/forum/ext/geomar/texintegr/latexrender/pictures/df6a970b0c06ad5e5858bf5f473ab167.png) ,
, 
Από την (4.2) προκύπτει ότι η αναμενόμενη τιμή της τυχαίας μεταβλητής V είναι:
![\displaystyle{E\left( V \right) = \mathop Z\limits_{t = 0}^n \left( \begin{array}{l}n \\ t \\\end{array} \right)\left( {1 - p} \right)^t p^{n - t} \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \displaystyle{E\left( V \right) = \mathop Z\limits_{t = 0}^n \left( \begin{array}{l}n \\ t \\\end{array} \right)\left( {1 - p} \right)^t p^{n - t} \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/b66458af6b0790bd7adfcc596272baf5.png)
Η αναμενόμενη τιμή γράφεται:
![\displaystyle{E\left( V \right) = \frac{1}{{\left( {1 + i} \right)^n }}\mathop Z\limits_{t = 0}^n \left( \begin{array}{l}n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \displaystyle{E\left( V \right) = \frac{1}{{\left( {1 + i} \right)^n }}\mathop Z\limits_{t = 0}^n \left( \begin{array}{l}n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/6eeda6a9c9e67a5fe24ee4e7bcc96e35.png)
ΒΙΒΛΙΟΓΡΑΦΙΑ
[1] Brealy, R.A. and Myers, S.C. Principles of Corporate Finance, Third Edition, McGraw-Hill Inc. 1988.
[2] Cox, J.C. Ross, S.A. and Rubinstein, M. Option Pricing: A Simplified Approa Journal,of Financial Economics.
[3] Kellison, S.G. The Theory of Interest, Second Edition, R.D. Irwin, Inc. 1991.
[4] Καρακιουλάφης , X. «Κίνδυνος και Χρησιμότητα των Χρηματοπιστωτικών Εργαλείων», Οικονομικά Χρονικά, Ιανουάριος 1995, 8-49.
[5] McCutcheon, J.J. and Scott, W.F.,«An Introduction to the Mathematics of Finance», Heinemann: London, 1986
[6] Miller, R.B. and Wichern, D.W., «Intermediate Business Statistics», HoltRinerhart and Winstone, 1977
με εκτίμηση
Γιάννης Κερασαρίδης
πηγή: η εργασία των Αναστασίου Σουγιάννη [πανεπ. Πειραιά] και Θανάση Μπελά [πανεπ. Πάτρας] (Μ.Ε. τεύχος 43, εκδόσεις ΕΜΕ)
Πολύς λόγος γίνεται τελευταία για τα χρηματοοικονομικά τερτίπια της διεθνούς τοκογλυφίας. Αναφερόμαστε, προφανώς, στα "χρηματοοικονομικά παράγωγα". Η εργασία που ακολουθεί αναφέρεται στο ευρωπαϊκό χρηματοοικονομικό δικαίωμα και συναφή θέματα:
25ο ΣΗΜΕΙΩΜΑ
"ΕΝΑ ΜΟΝΤΕΛΟ ΤΗΣ ΑΝΑΜΕΝΟΜΕΝΗΣ ΑΡΧΙΚΗΣ ΑΞΙΑΣ ΤΟΥ ΕΥΡΩΠΑΪΚΟΥ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΟΥ ΔΙΚΑΙΩΜΑΤΟΣ"[/i][/color][/b]
ΑΝΑΣΤΑΣΙΟΥ ΣΟΥΠΑΝΝΗ ΑΘΑΝΑΣΙΟΥ ΜΠΕΛΛΑ
ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΙΡΑΙΩΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΑΣ
1. Εισαγωγή
Τα παράγωγα χρηματοοικονομικά εργαλεία [derivactive financial instruments] είναι χρηματοοικονομικά εργαλεία με τα οποία μπορεί κάποιος να κερδίσει ή να χάσει χρήματα προβλέποντας τις μεταβολές που θα έχουν οι τιμές διαφόρων αξιόγραφων ή προϊόντων. Τα παράγωγα αναπτύχτηκαν και χρησιμοποιούνται ως ένας τρόπος προστασίας των επιχειρήσεων και των επενδυτών από τις απότομες μεταβολές των τιμών στις αγορές συναλλάγματος, επιτοκίων, μετάλλων, και πρώτων υλών. Μια εισαγωγική επιχείρηση που πρόκειται να πληρώσει τις υποχρεώσεις της σε συνάλλαγμα μπορεί να κάνει χρήση ενός παράγωγου για να προφυλαχθεί από μια υποτίμηση συμφωνώντας να αγοράσει συνάλλαγμα την ημέρα της πληρωμής σε προκαθορισμένη τιμή. Η ανάπτυξη των παραγώγων υπήρξε πολύ γρήγορη διότι μετά την κατάργηση της συμφωνίας του Breton Woods και την ελεύθερη διακύμανση των συναλλαγματικών ισοτιμιών, οι χρηματοοικονομικές αγορές έγιναν πολύ ασταθείς. Η ανάγκη προστασίας από τους συναλλαγματικούς κινδύνους συνέβαλε στη γρήγορη ανάπτυξη των παραγωγών σε ομόλογα, νομίσματα ή μετοχές μετά τα μέσα της προηγούμενης δεκαετίας. Ένα σημαντικό πρόβλημα που αντιμετωπίζουν οι κεντρικές τράπεζες και οι κυβερνήσεις είναι ο τρόπος με τον οποίο οι μεγάλες διεθνείς τράπεζες χρησιμοποιούν τα παράγωγα, οι οποίες δεν διστάζουν να αναλάβουν μεγάλους κερδοσκοπικούς κινδύνους διαθέτοντας τεράστια ποσά στα παράγωγα εκμεταλλευόμενες το μικρό κόστος των εργαλείων αυτών[1].
Σύμφωνα με τα ευρήματα εμπειρικών μελετών στις πράξεις των παραγώγων υπεισέρχονται παράγοντες, οι οποίοι δημιουργούν προβλήματα στη Διοίκηση Κινδύνου [Risk Management], όπως:
Περιορισμένη εμπειρία των συμμετεχόντων - Περιπλοκότητα των πράξεων των παραγώγων - Ελκυστικότητα του βραχυχρόνιου κέρδους - Παραγνώριση των κινδύνων λόγω βραχυχρόνιου κέρδους. Επειδή στις πράξεις των παραγώγων οι συμμετέχοντες δεν έχουν την δυνατότητα ή δεν θέλουν να ανακαλύψουν τους κινδύνους τότε θεωρείται απαραίτητη η λήψη ορισμένων μέτρων, όπως:
— Δημιουργία νέου νομοθετικού αυστηρού πλαισίου που θα θεσμοθετεί τους κανόνες λειτουργίας των πράξεων των παραγώγων.
— Διεξαγωγή των πράξεων των παραγώγων μόνο από τράπεζες με υποχρέωση ανακοίνωσης των πράξεων αυτών στη κεντρική τράπεζα με σύγχρονη αλλαγή στον τρόπο λογιστικοποίησης αυτών
— Καλύτερη οργάνωση των τραπεζών στον τομέα της Διοίκησης Κινδύνου και εκπαίδευση του προσωπικού στον τομέα των παραγώγων.
— Ανάπτυξη νέων μεθόδων στις διαδικασίες λήψης αποφάσεων σχετικά με τα παράγωγα, δηλαδή κατασκευή μοντέλων που θα δίνουν τη δυνατότητα ευκολότερης και καλύτερης ποσοτικής ανάλυσης των κινδύνων [ 4 ].
Σκοπός της εργασίας αυτής είναι να παρουσιάσει ένα μοντέλο για τη λήψη αποφάσεων σχετικά με το Ευρωπαϊκό χρηματοοικονομικό δικαίωμα το οποίο είναι ένα παράγωγο χρηματοοικονομικό εργαλείο.
2. Χρηματοοικονομικό Δικαίωμα
Το χρηματοοικονομικό δικαίωμα [option] είναι ένα χρηματοοικονομικό εργαλείο το οποίο δίνει στον κάτοχό του το δικαίωμα, χωρίς υποχρέωση , αγοράς ή πώλησης ενός αξιόγραφου ή προϊόντος σε μια μελλοντική χρονική στιγμή και σε μια προκαθορισμένη τιμή η οποία λέγεται τιμή άσκησης δικαιώματος. Το δικαίωμα αυτό ισχύει για ένα χρονικό διάστημα που ορίζεται κατά την αγορά του χρηματοοικονομικού δικαιώματος. Το τέλος του χρονικού αυτού διαστήματος λέγεται λήξη του χρηματοοικονομικού δικαιώματος. Υπάρχουν δυο τύποι χρηματοοικονομικών δικαιωμάτων : Το χρηματοοικονομικό δικαίωμα αγοράς το οποίο δίνει στον κάτοχο του το δικαίωμα αγοράς ενός αξιόγραφου ή προϊόντος στην προκαθορισμένη τιμή και το χρηματοοικονομικό δικαίωμα πώλησης το οποίο δίνει στον κάτοχό του το δικαίωμα πώλησης ενός αξιόγραφου ή προϊόντος στην προκαθορισμένη τιμή, είναι προφανές ότι στην λήξη ενός χρηματοοικονομικού δικαιώματος, ο κάτοχός του έχει την δυνατότητα να χρησιμοποιήσει το "δικαίωμα" , δηλαδή να αγοράσει ή να πουλήσει το αξιόγραφο ή το αγαθό, μόνο αν η τιμή είναι συμφέρουσα γι αυτόν.
Στην αντίθετη περίπτωση δεν το κάνει και το χρηματοοικονομικό δικαίωμα λήγει. Σύμφωνα με το Ευρωπαϊκό χρηματοοικονομικό δικαίωμα η άσκηση του δικαιώματος πώλησης ή αγοράς γίνεται κατά τη Λήξη του χρηματοοικονομικού δικαιώματος. Σύμφωνα όμως με το Αμερικάνικο χρηματοοικονομικό δικαίωμα η άσκηση του δικαιώματος αγοράς ή πώλησης μπορεί να γίνει σε οποιαδήποτε χρονική στιγμή του χρονικού διαστήματος που ορίζεται από τη χρονική στιγμή αγοράς και τη χρονική στιγμή λήξης του χρηματοοικονομικού δικαιώματος [2].
Σκοπός της εργασίας αυτής είναι να παρουσιάσει με κάθε δυνατή λεπτομέρεια ένα μοντέλο υπολογισμού της αναμενόμενης αρχικής αξίας του Ευρωπαϊκού χρηματοοικονομικού δικαιώματος [3].
3. Υποθέσεις του Μοντέλου
Σκοπός του τρίτου μέρους της εργασίας είναι, να παρουσιάσει τις υποθέσεις στις οποίες βασίζεται το μοντέλο που αναπτύσσεται στο τέταρτο μέρος της εργασίας.
Το χρονικό διάστημα [που ορίζεται από τη χρονική στιγμή αγοράς και τη χρονική στιγμή της λήξης του χρηματοοικονομικού δικαιώματος χωρίζεται σε η ίσες χρονικές περιόδους. Το επιτόκιο κάθε χρονικής περιόδου είναι i και η τιμή αγοράς του αξιόγραφου κατά την χρονική στιγμή είναι 0 είναι S. Κατά τη διάρκεια μιας χρονικής περιόδου η τιμή του αξιόγραφου αυξάνεται με πιθανότητα p ή μειώνεται με πιθανότητα
 .
. Αύξηση της τιμής του αξιόγραφου κατά τη διάρκεια μιας χρονικής περιόδου σημαίνει ότι η τιμή του αξιόγραφου στο τέλος της χρονικής περιόδου είναι το αποτέλεσμα του πολλαπλασιασμού της τιμής του αξιόγραφου στην αρχή της χρονικής περιόδου με τον παράγοντα
 , όπου
, όπου 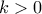 . Μείωση της τιμής του αξιόγραφου κατά τη διάρκεια μιας χρονικής περιόδου σημαίνει ότι η τιμή του αξιόγραφου στο τέλος της χρονικής περιόδου είναι το αποτέλεσμα του πολλαπλασιασμού της τιμής του αξιόγραφου στην αρχή της περιόδου με τον παράγοντα
. Μείωση της τιμής του αξιόγραφου κατά τη διάρκεια μιας χρονικής περιόδου σημαίνει ότι η τιμή του αξιόγραφου στο τέλος της χρονικής περιόδου είναι το αποτέλεσμα του πολλαπλασιασμού της τιμής του αξιόγραφου στην αρχή της περιόδου με τον παράγοντα  ,
, 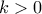
Η αύξηση ή η μείωση της τιμής του αξιόγραφου σε μια χρονική περίοδο είναι ανεξάρτητη από την αύξηση ή μείωση της τιμής του αξιόγραφου σε κάθε άλλη χρονική περίοδο.
4. Ανάπτυξη του Μοντέλου
Έστω Τ τυχαία μεταβλητή η οποία παριστάνει τον αριθμό των χρονικών περιόδων στις οποίες μειώθηκε η τιμή του αξιόγραφου. Η τυχαία μεταβλητή Τ παίρνει τις τιμές 0,1,…, η.
Η πιθανότητα αύξησης της τιμής του αξιόγραφου σε κάποια χρονική περίοδο είναι p και
 είναι η πιθανότητα μείωσης της τιμής του αξιόγραφου στην ίδια χρονική περίοδο. Επειδή η μείωση ή η αύξηση της τιμής του αξιόγραφου σε κάποια χρονική περίοδο είναι ανεξάρτητη από τη μείωση ή αύξηση της τιμής του αξιόγραφου σε κάθε άλλη χρονική περίοδο τότε η τυχαία μεταβλητή Τ ακολουθεί τη διωνυμική κατανομή [ 6 ].
είναι η πιθανότητα μείωσης της τιμής του αξιόγραφου στην ίδια χρονική περίοδο. Επειδή η μείωση ή η αύξηση της τιμής του αξιόγραφου σε κάποια χρονική περίοδο είναι ανεξάρτητη από τη μείωση ή αύξηση της τιμής του αξιόγραφου σε κάθε άλλη χρονική περίοδο τότε η τυχαία μεταβλητή Τ ακολουθεί τη διωνυμική κατανομή [ 6 ]. Η συνάρτηση πιθανότητας της τυχαίας μεταβλητής Τ είναι :
![\displaystyle{P\left[ {T = t} \right] = \left( \begin{array}{l}n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} } \displaystyle{P\left[ {T = t} \right] = \left( \begin{array}{l}n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} }](/forum/ext/geomar/texintegr/latexrender/pictures/a9361565f3362d8dbb30fcf3f173f25b.png) ,
, 
Υποθέτουμε ότι
 τότε η τιμή του αξιόγραφου κατά τη χρονική στιγμή n, η οποία είναι η στιγμή λήξης του χρηματοοικονομικού δικαιώματος, είναι
τότε η τιμή του αξιόγραφου κατά τη χρονική στιγμή n, η οποία είναι η στιγμή λήξης του χρηματοοικονομικού δικαιώματος, είναι 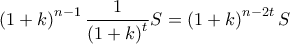
διότι η τιμή του αξιόγραφου αυξήθηκε σε
 χρονικές περιόδους και μειώθηκε σε i χρονικές περιόδους [ 5 ]. Συμβολίζουμε με Ε την τιμή άσκησης του δικαιώματος. Αν
χρονικές περιόδους και μειώθηκε σε i χρονικές περιόδους [ 5 ]. Συμβολίζουμε με Ε την τιμή άσκησης του δικαιώματος. Αν ,
, 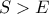
τότε η αξία του αξιόγραφου κατά την χρονική στιγμή η είναι:

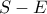
Αν

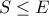
τότε η αξία του αξιόγραφου κατά την χρονική στιγμή η είναι 0. Επομένως η αξία του αξιόγραφου κατά την χρονική στιγμή η είναι:
![\displaystyle{\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \displaystyle{\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/b2bdbc7123863a940e02b84e85742951.png)
και
![\displaystyle{\frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1+k} \right)^{n - 2t} S - E} \right]} \displaystyle{\frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1+k} \right)^{n - 2t} S - E} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/1d838c2df6d737149c30e94d74e8ea9e.png)
είναι η αρχική αξία του αξιόγραφου κατά την χρονική στιγμή 0 όταν
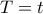 .
. Έστω V τυχαία μεταβλητή η οποία παριστάνει την αρχική αξία του αξιόγραφου κατά την χρονική στιγμή 0. Το ενδεχόμενο
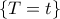 , συνεπάγεται το ενδεχόμενο
, συνεπάγεται το ενδεχόμενο![\displaystyle{\left\{ {V = \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \right\}} \displaystyle{\left\{ {V = \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \right\}}](/forum/ext/geomar/texintegr/latexrender/pictures/bf5d16119bbeceb62f4a1827f9a8879e.png)
και αντίστροφα. Επομένως από την (4.1) έχουμε:
![\displaystyle{P\left\{ {V = \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \right\} = P\left[ {T = t} \right] = \[\left( \begin{array}{l} n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} } \displaystyle{P\left\{ {V = \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \right\} = P\left[ {T = t} \right] = \[\left( \begin{array}{l} n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} }](/forum/ext/geomar/texintegr/latexrender/pictures/df6a970b0c06ad5e5858bf5f473ab167.png) ,
, 
Από την (4.2) προκύπτει ότι η αναμενόμενη τιμή της τυχαίας μεταβλητής V είναι:
![\displaystyle{E\left( V \right) = \mathop Z\limits_{t = 0}^n \left( \begin{array}{l}n \\ t \\\end{array} \right)\left( {1 - p} \right)^t p^{n - t} \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \displaystyle{E\left( V \right) = \mathop Z\limits_{t = 0}^n \left( \begin{array}{l}n \\ t \\\end{array} \right)\left( {1 - p} \right)^t p^{n - t} \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/b66458af6b0790bd7adfcc596272baf5.png)
Η αναμενόμενη τιμή γράφεται:
![\displaystyle{E\left( V \right) = \frac{1}{{\left( {1 + i} \right)^n }}\mathop Z\limits_{t = 0}^n \left( \begin{array}{l}n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]} \displaystyle{E\left( V \right) = \frac{1}{{\left( {1 + i} \right)^n }}\mathop Z\limits_{t = 0}^n \left( \begin{array}{l}n \\ t \\ \end{array} \right)\left( {1 - p} \right)^t p^{n - t} \frac{1}{{\left( {1 + i} \right)^n }}\max \left[ {0,\left( {1 + k} \right)^{n - 2t} S - E} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/6eeda6a9c9e67a5fe24ee4e7bcc96e35.png)
ΒΙΒΛΙΟΓΡΑΦΙΑ
[1] Brealy, R.A. and Myers, S.C. Principles of Corporate Finance, Third Edition, McGraw-Hill Inc. 1988.
[2] Cox, J.C. Ross, S.A. and Rubinstein, M. Option Pricing: A Simplified Approa Journal,of Financial Economics.
[3] Kellison, S.G. The Theory of Interest, Second Edition, R.D. Irwin, Inc. 1991.
[4] Καρακιουλάφης , X. «Κίνδυνος και Χρησιμότητα των Χρηματοπιστωτικών Εργαλείων», Οικονομικά Χρονικά, Ιανουάριος 1995, 8-49.
[5] McCutcheon, J.J. and Scott, W.F.,«An Introduction to the Mathematics of Finance», Heinemann: London, 1986
[6] Miller, R.B. and Wichern, D.W., «Intermediate Business Statistics», HoltRinerhart and Winstone, 1977
με εκτίμηση
Γιάννης Κερασαρίδης
πηγή: η εργασία των Αναστασίου Σουγιάννη [πανεπ. Πειραιά] και Θανάση Μπελά [πανεπ. Πάτρας] (Μ.Ε. τεύχος 43, εκδόσεις ΕΜΕ)
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
Προλεγόμενα Σ’ αυτό το σημείωμα θα δούμε πως η μαθηματική σκέψη συνδέεται με καταστάσεις κατά τις οποίες πρέπει να πάρουμε την βέλτιστη δυνατή απόφαση. Υπάρχει ένας κλάδος των Μαθηματικών, η Θεωρία Αποφάσεων, που αναφέρεται σε αλγόριθμους με βάση τους οποίους μπορούμε να πάρουμε τη βέλτιστη δυνατή απόφαση. Παρουσιάζουμε ένα τμήμα της μεταπτυχιακής εργασίας της Αγγελικής Βουδούρη
26ο ΣΗΜΕΙΩΜΑ
ΕΦΑΡΜΟΓΕΣ ΔΙΩΝΥΜΙΚΩΝ ΤΥΧΑΙΩΝ ΑΘΡΟΙΣΜΑΤΩΝ
ΣΤΗ ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ
ΑΓΓΕΛΙΚΗ ΒΟΥΔΟΥΡΗ
«1. Εισαγωγή
Μια απόφαση είναι το συμπέρασμα μιας διαδικασίας στάθμισης των σχετικών χρησιμοτήτων ενός συνόλου διαθέσιμων εναλλακτικών τρόπων δράσης με σκοπό να επιλεγεί ο πλέον επιθυμητός τρόπος δράσης. Η λήψη αποφάσεων περιλαμβάνει όλες τις δραστηριότητες που απαιτούνται για τον προσδιορισμό του πλέον επιθυμητού τρόπου δράσης. Οι αποφάσεις λαμβάνονται επειδή οι φυσικοί πόροι είναι σπάνιοι και επειδή οι άνθρωποι έχουν επιθυμίες και ανάγκες.
Η θεωρία αποφάσεων —το σύνολο των γνώσεων που σχετίζεται με την ανάλυση και λήψη αποφάσεων— είναι μια πολύ σημαντική περιοχή μελέτης. Αυτό είναι προφανές από τις συμβολές διαφόρων γνωστικών πεδίων, όπως είναι η φιλοσοφία, ψυχολογία, κοινωνιολογία, οικονομική επιστήμη, πολιτική επιστήμη και επιχειρησιακή έρευνα, στην περιοχή της θεωρίας αποφάσεων. Η λήψη αποφάσεων κάτω από συνθήκες αβεβαιότητας περιγράφει μια κατάσταση στην οποία όλη η σχετική πληροφορία που απαιτείται για τη λήψη μιας απόφασης δεν είναι γνωστή με βεβαιότητα. Επειδή ο άνθρωπος αντιμετωπίζει συχνότατα καταστάσεις μη πλήρους βεβαιότητας ή ισοδύναμα καταστάσεις αβεβαιότητας και επειδή η θεωρία πιθανοτήτων είναι η μελέτη τέτοιων καταστάσεων προκύπτει ότι η συμβολή της θεωρίας πιθανοτήτων στη λήψη αποφάσεων είναι πολύ σημαντική.
Σκοπός της εργασίας αυτής είναι να παρουσιάσει εφαρμογές του διωνυμικού τυχαίου αθροίσματος, η οποία είναι μια βασική έννοια της θεωρίας πιθανοτήτων, στη λήψη αποφάσεων κάτω από συνθήκες αβεβαιότητας.
2. Λήψη Αποφάσεων κάτω από Συνθήκες Αβεβαιότητας
Στη διαδικασία λήψης αποφάσεων κάτω από συνθήκες αβεβαιότητας υπεισέρχονται τα ακόλουθα σύνολα. Το σύνολο Α των τρόπων δράσης, το σύνολο Β των καταστάσεων και το σύνολο Ο των αποτελεσμάτων. Τα στοιχεία του συνόλου Α είναι οι διαφορετικοί τρόποι δράσης ενός ατόμου. Η επιλογή ενός τρόπου δράσης είναι μια απόφαση. Το άτομο μπορεί να επιλέξει μόνο ένα τρόπο δράσης. Τα στοιχεία του συνόλου Β είναι τυχαίες μεταβλητές που περιγράφουν παράγοντες οι οποίοι υπεισέρχονται στη διαμόρφωση των αποτελεσμάτων των αποφάσεων. Τα στοιχεία του συνόλου Ο είναι τυχαίες μεταβλητές που περιγράφουν τα αποτελέσματα των αποφάσεων. Μια απόφαση και όλα τα στοιχεία του συνόλου Β υπεισέρχονται στον ορισμό ενός στοιχείου του συνόλου O.
Η λήψη μιας απόφασης —η επιλογή ενός τρόπου δράσης— απαιτεί τη χρήση ενός κριτηρίου ή περισσοτέρων κριτηρίων. Ένα κριτήριο είναι ένας κανόνας με τον οποίο επιλέγεται ένας τρόπος δράσης. Η διαδικασία λήψης αποφάσεων κάτω από συνθήκες αβεβαιότητας χρησιμοποιεί συνήθως το κριτήριο της αναμενόμενης τιμής και το κριτήριο της αναμενόμενης χρησιμότητας. Η θεωρία αποφάσεων υποστηρίζει τη χρήση του κριτηρίου της αναμενόμενης χρησιμότητας. Το μόνο πλεονέκτημα που παρουσιάζει το κριτήριο της αναμενόμενης τιμής είναι η απλότητα. Το πλεονέκτημα αυτό είναι μερικές φορές αρκετό για τη χρήση του κριτηρίου της αναμενόμενης τιμής στη λήψη αποφάσεων κάτω από συνθήκες αβεβαιότητας [3].
3. Τυχαία Αθροίσματα
Έστω ακολουθία ανεξαρτήτων τυχαίων μεταβλητών με συνάρτηση κατανομής
ακολουθία ανεξαρτήτων τυχαίων μεταβλητών με συνάρτηση κατανομής  . Συμβολίζουμε με
. Συμβολίζουμε με  τη συνάρτηση κατανομής της τυχαίας μεταβλητής
τη συνάρτηση κατανομής της τυχαίας μεταβλητής  . Έστω Ν διακριτή τυχαία μεταβλητή ανεξάρτητη των
. Έστω Ν διακριτή τυχαία μεταβλητή ανεξάρτητη των 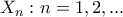 με συνάρτηση πιθανότητας
με συνάρτηση πιθανότητας
![\displaystyle{P\left[ {N = n} \right] = p_n ,} \displaystyle{P\left[ {N = n} \right] = p_n ,}](/forum/ext/geomar/texintegr/latexrender/pictures/d079625e5913f5340aa7f2cc0cc28c6e.png)

Η τυχαία μεταβλητή (3.1)
(3.1)
λέγεται τυχαίο άθροισμα, Feller [2]. Επειδή είναι η συνάρτηση κατανομής της τυχαίας μεταβλητής s όταν
είναι η συνάρτηση κατανομής της τυχαίας μεταβλητής s όταν  τότε:
τότε:
![\displaystyle{\begin{array}{l}F_s \left( s \right) = P\left[ {S \le s} \right] = \\ \sum\limits_{n = 0}^\infty {P\left[ {S \le s\left| {N = n} \right.} \right]} P\left[ {N = n} \right] = \sum\limits_{n = 0}^\infty {p_n } F_x^{\left( n \right)} \left( s \right) \\ \end{array}} \displaystyle{\begin{array}{l}F_s \left( s \right) = P\left[ {S \le s} \right] = \\ \sum\limits_{n = 0}^\infty {P\left[ {S \le s\left| {N = n} \right.} \right]} P\left[ {N = n} \right] = \sum\limits_{n = 0}^\infty {p_n } F_x^{\left( n \right)} \left( s \right) \\ \end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/a7f2f1d5741dc101d0ff438179f79197.png) (3.2)
(3.2)
είναι η συνάρτηση κατανομής του τυχαίου αθροίσματος s. Επειδή η συνάρτηση κατανομής του τυχαίου αθροίσματος s είναι πολύ περίπλοκη, η μελέτη των τυχαίων αθροισμάτων γίνεται συχνά με τη χρήση χαρακτηριστικών συναρτήσεων.
του τυχαίου αθροίσματος s είναι πολύ περίπλοκη, η μελέτη των τυχαίων αθροισμάτων γίνεται συχνά με τη χρήση χαρακτηριστικών συναρτήσεων.
Έστω
![\displaystyle{\varphi _x \left( u \right) = E\left[ {e^{iux} } \right]} \displaystyle{\varphi _x \left( u \right) = E\left[ {e^{iux} } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/620c18b712b74f09d3048d590c55bac4.png) ,
, 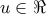
η χαρακτηριστική συνάρτηση της συνάρτησης κατανομής και
και ![\displaystyle{P_n \left( z \right) = E\left[ {z^N } \right],} \displaystyle{P_n \left( z \right) = E\left[ {z^N } \right],}](/forum/ext/geomar/texintegr/latexrender/pictures/3ee3369d966854a57b77746d8aee61a9.png)

η πιθανογεννήτρια συνάρτηση της τυχαίας μεταβλητής Ν. Επειδή είναι η χαρακτηριστική συνάρτηση της συνάρτησης κατανομής
είναι η χαρακτηριστική συνάρτηση της συνάρτησης κατανομής  τότε
τότε
![\displaystyle{\varphi _s \left( u \right) = E\left[ {e^{ius} } \right] = \sum\limits_{n = 0}^\infty {E\left[ {e^{ius} \left| {N = n} \right.} \right]} P\left[ {N = n} \right]} \displaystyle{\varphi _s \left( u \right) = E\left[ {e^{ius} } \right] = \sum\limits_{n = 0}^\infty {E\left[ {e^{ius} \left| {N = n} \right.} \right]} P\left[ {N = n} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/13f4c071c7913c35e3a6dd996cfa062c.png) )
)  είναι η χαρακτηριστική συνάρτηση του τυχαίου αθροίσματος s.
είναι η χαρακτηριστική συνάρτηση του τυχαίου αθροίσματος s.
Τα τυχαία αθροίσματα έχουν σημαντικότατες εφαρμογές στα συστήματα εξυπηρέτησης, στη θεωρία κινδύνου, στη χρηματοοικονομική διοίκηση και σε πολλά άλλα γνωστικά πεδία, [4]»
...........................................................................................................................................
«Βιβλιογραφία
1. Artikis, T. Jerwood, D. On the Unimodality of Present Value Distributions, European J. Operational Res., to appear
2.Feller, W. An Introduction to Probabilty Theory and its Applications, Vol. 2, 1971, John Wiley, New York
3.Mao, J. Quantitative Analysis of Financial Decisions, 1969, Macmillan, New York
4.Takacs, L. Stochastic Processes, 1966, Methuen, London»
26ο ΣΗΜΕΙΩΜΑ
ΕΦΑΡΜΟΓΕΣ ΔΙΩΝΥΜΙΚΩΝ ΤΥΧΑΙΩΝ ΑΘΡΟΙΣΜΑΤΩΝ
ΣΤΗ ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ
ΑΓΓΕΛΙΚΗ ΒΟΥΔΟΥΡΗ
«1. Εισαγωγή
Μια απόφαση είναι το συμπέρασμα μιας διαδικασίας στάθμισης των σχετικών χρησιμοτήτων ενός συνόλου διαθέσιμων εναλλακτικών τρόπων δράσης με σκοπό να επιλεγεί ο πλέον επιθυμητός τρόπος δράσης. Η λήψη αποφάσεων περιλαμβάνει όλες τις δραστηριότητες που απαιτούνται για τον προσδιορισμό του πλέον επιθυμητού τρόπου δράσης. Οι αποφάσεις λαμβάνονται επειδή οι φυσικοί πόροι είναι σπάνιοι και επειδή οι άνθρωποι έχουν επιθυμίες και ανάγκες.
Η θεωρία αποφάσεων —το σύνολο των γνώσεων που σχετίζεται με την ανάλυση και λήψη αποφάσεων— είναι μια πολύ σημαντική περιοχή μελέτης. Αυτό είναι προφανές από τις συμβολές διαφόρων γνωστικών πεδίων, όπως είναι η φιλοσοφία, ψυχολογία, κοινωνιολογία, οικονομική επιστήμη, πολιτική επιστήμη και επιχειρησιακή έρευνα, στην περιοχή της θεωρίας αποφάσεων. Η λήψη αποφάσεων κάτω από συνθήκες αβεβαιότητας περιγράφει μια κατάσταση στην οποία όλη η σχετική πληροφορία που απαιτείται για τη λήψη μιας απόφασης δεν είναι γνωστή με βεβαιότητα. Επειδή ο άνθρωπος αντιμετωπίζει συχνότατα καταστάσεις μη πλήρους βεβαιότητας ή ισοδύναμα καταστάσεις αβεβαιότητας και επειδή η θεωρία πιθανοτήτων είναι η μελέτη τέτοιων καταστάσεων προκύπτει ότι η συμβολή της θεωρίας πιθανοτήτων στη λήψη αποφάσεων είναι πολύ σημαντική.
Σκοπός της εργασίας αυτής είναι να παρουσιάσει εφαρμογές του διωνυμικού τυχαίου αθροίσματος, η οποία είναι μια βασική έννοια της θεωρίας πιθανοτήτων, στη λήψη αποφάσεων κάτω από συνθήκες αβεβαιότητας.
2. Λήψη Αποφάσεων κάτω από Συνθήκες Αβεβαιότητας
Στη διαδικασία λήψης αποφάσεων κάτω από συνθήκες αβεβαιότητας υπεισέρχονται τα ακόλουθα σύνολα. Το σύνολο Α των τρόπων δράσης, το σύνολο Β των καταστάσεων και το σύνολο Ο των αποτελεσμάτων. Τα στοιχεία του συνόλου Α είναι οι διαφορετικοί τρόποι δράσης ενός ατόμου. Η επιλογή ενός τρόπου δράσης είναι μια απόφαση. Το άτομο μπορεί να επιλέξει μόνο ένα τρόπο δράσης. Τα στοιχεία του συνόλου Β είναι τυχαίες μεταβλητές που περιγράφουν παράγοντες οι οποίοι υπεισέρχονται στη διαμόρφωση των αποτελεσμάτων των αποφάσεων. Τα στοιχεία του συνόλου Ο είναι τυχαίες μεταβλητές που περιγράφουν τα αποτελέσματα των αποφάσεων. Μια απόφαση και όλα τα στοιχεία του συνόλου Β υπεισέρχονται στον ορισμό ενός στοιχείου του συνόλου O.
Η λήψη μιας απόφασης —η επιλογή ενός τρόπου δράσης— απαιτεί τη χρήση ενός κριτηρίου ή περισσοτέρων κριτηρίων. Ένα κριτήριο είναι ένας κανόνας με τον οποίο επιλέγεται ένας τρόπος δράσης. Η διαδικασία λήψης αποφάσεων κάτω από συνθήκες αβεβαιότητας χρησιμοποιεί συνήθως το κριτήριο της αναμενόμενης τιμής και το κριτήριο της αναμενόμενης χρησιμότητας. Η θεωρία αποφάσεων υποστηρίζει τη χρήση του κριτηρίου της αναμενόμενης χρησιμότητας. Το μόνο πλεονέκτημα που παρουσιάζει το κριτήριο της αναμενόμενης τιμής είναι η απλότητα. Το πλεονέκτημα αυτό είναι μερικές φορές αρκετό για τη χρήση του κριτηρίου της αναμενόμενης τιμής στη λήψη αποφάσεων κάτω από συνθήκες αβεβαιότητας [3].
3. Τυχαία Αθροίσματα
Έστω
 ακολουθία ανεξαρτήτων τυχαίων μεταβλητών με συνάρτηση κατανομής
ακολουθία ανεξαρτήτων τυχαίων μεταβλητών με συνάρτηση κατανομής  . Συμβολίζουμε με
. Συμβολίζουμε με  τη συνάρτηση κατανομής της τυχαίας μεταβλητής
τη συνάρτηση κατανομής της τυχαίας μεταβλητής  . Έστω Ν διακριτή τυχαία μεταβλητή ανεξάρτητη των
. Έστω Ν διακριτή τυχαία μεταβλητή ανεξάρτητη των 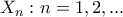 με συνάρτηση πιθανότητας
με συνάρτηση πιθανότητας ![\displaystyle{P\left[ {N = n} \right] = p_n ,} \displaystyle{P\left[ {N = n} \right] = p_n ,}](/forum/ext/geomar/texintegr/latexrender/pictures/d079625e5913f5340aa7f2cc0cc28c6e.png)

Η τυχαία μεταβλητή
 (3.1)
(3.1) λέγεται τυχαίο άθροισμα, Feller [2]. Επειδή
 είναι η συνάρτηση κατανομής της τυχαίας μεταβλητής s όταν
είναι η συνάρτηση κατανομής της τυχαίας μεταβλητής s όταν  τότε:
τότε: ![\displaystyle{\begin{array}{l}F_s \left( s \right) = P\left[ {S \le s} \right] = \\ \sum\limits_{n = 0}^\infty {P\left[ {S \le s\left| {N = n} \right.} \right]} P\left[ {N = n} \right] = \sum\limits_{n = 0}^\infty {p_n } F_x^{\left( n \right)} \left( s \right) \\ \end{array}} \displaystyle{\begin{array}{l}F_s \left( s \right) = P\left[ {S \le s} \right] = \\ \sum\limits_{n = 0}^\infty {P\left[ {S \le s\left| {N = n} \right.} \right]} P\left[ {N = n} \right] = \sum\limits_{n = 0}^\infty {p_n } F_x^{\left( n \right)} \left( s \right) \\ \end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/a7f2f1d5741dc101d0ff438179f79197.png) (3.2)
(3.2)είναι η συνάρτηση κατανομής του τυχαίου αθροίσματος s. Επειδή η συνάρτηση κατανομής
 του τυχαίου αθροίσματος s είναι πολύ περίπλοκη, η μελέτη των τυχαίων αθροισμάτων γίνεται συχνά με τη χρήση χαρακτηριστικών συναρτήσεων.
του τυχαίου αθροίσματος s είναι πολύ περίπλοκη, η μελέτη των τυχαίων αθροισμάτων γίνεται συχνά με τη χρήση χαρακτηριστικών συναρτήσεων. Έστω
![\displaystyle{\varphi _x \left( u \right) = E\left[ {e^{iux} } \right]} \displaystyle{\varphi _x \left( u \right) = E\left[ {e^{iux} } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/620c18b712b74f09d3048d590c55bac4.png) ,
, 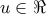
η χαρακτηριστική συνάρτηση της συνάρτησης κατανομής
 και
και ![\displaystyle{P_n \left( z \right) = E\left[ {z^N } \right],} \displaystyle{P_n \left( z \right) = E\left[ {z^N } \right],}](/forum/ext/geomar/texintegr/latexrender/pictures/3ee3369d966854a57b77746d8aee61a9.png)

η πιθανογεννήτρια συνάρτηση της τυχαίας μεταβλητής Ν. Επειδή
 είναι η χαρακτηριστική συνάρτηση της συνάρτησης κατανομής
είναι η χαρακτηριστική συνάρτηση της συνάρτησης κατανομής  τότε
τότε ![\displaystyle{\varphi _s \left( u \right) = E\left[ {e^{ius} } \right] = \sum\limits_{n = 0}^\infty {E\left[ {e^{ius} \left| {N = n} \right.} \right]} P\left[ {N = n} \right]} \displaystyle{\varphi _s \left( u \right) = E\left[ {e^{ius} } \right] = \sum\limits_{n = 0}^\infty {E\left[ {e^{ius} \left| {N = n} \right.} \right]} P\left[ {N = n} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/13f4c071c7913c35e3a6dd996cfa062c.png) )
)  είναι η χαρακτηριστική συνάρτηση του τυχαίου αθροίσματος s.
είναι η χαρακτηριστική συνάρτηση του τυχαίου αθροίσματος s. Τα τυχαία αθροίσματα έχουν σημαντικότατες εφαρμογές στα συστήματα εξυπηρέτησης, στη θεωρία κινδύνου, στη χρηματοοικονομική διοίκηση και σε πολλά άλλα γνωστικά πεδία, [4]»
...........................................................................................................................................
«Βιβλιογραφία
1. Artikis, T. Jerwood, D. On the Unimodality of Present Value Distributions, European J. Operational Res., to appear
2.Feller, W. An Introduction to Probabilty Theory and its Applications, Vol. 2, 1971, John Wiley, New York
3.Mao, J. Quantitative Analysis of Financial Decisions, 1969, Macmillan, New York
4.Takacs, L. Stochastic Processes, 1966, Methuen, London»
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
27ο ΣΗΜΕΙΩΜΑ
«ΟΠΟΙΟΣ ΞΕΡΕΙ ΚΑΛΑ ΜΑΘΗΜΑΤΙΚΑ ΞΕΡΕΙ ΚΑΙ ΚΑΛΟ...ΜΠΑΣΚΕΤ;»
Προλεγόμενα Χθες με επισκέφθηκε ένας καλός φίλος Γυμναστής. Ανάμεσα στα άλλα μου θύμισε ένα παλιό σημείωμα που είχα δημοσιεύσει με θέμα το μπάσκετ. Με αφορμή αυτή την υπενθύμιση, σκέφθηκα να αναδημοσιεύσω εκείνο το σημείωμα. Σας το παρουσιάζω όπως είχε δημοσιευθεί τότε. Ο «Γυμναστής» εκείνου του σημειώματος είναι ο φίλος που με επισκέφθηκε.
Το δημοσίευμα εκείνο
«Προ καιρού ένας καλός φίλος Γυμναστής, που ασχολείται με τα σπορ με τόση επιμέλεια, όση και ο ζήλος του Gauss για τα Μαθηματικά, μας ξάφνιασε όταν μας είπε πως, σε ένα σεμινάριο που έλαβε μέρος, άκουσε ότι τα Μαθηματικά χρησιμεύουν για την μελέτη ενός από τα πιο δημοφιλή αθλήματα, του μπάσκετ. Ψάξαμε τη σχετική βιβλιογραφία. Από το θησαυρό πληροφοριών που βγήκε στην επιφάνεια διαλέξαμε αυτό που βρήκαμε στο έγκυρο επιστημονικό περιοδικό (βιβλιοθήκης), το "QUANTUM" (εκδόσεις "Κάτοπτρο"), με τίτλο: "Άλματα και καλαθιές, κινηματική στο γήπεδο του μπάσκετ" του Roman Vinokur (τόμος 2, τεύχος 5). Σας παρουσιάζουμε τα κυριότερα σημεία του.
Στο σχήμα που βλέπετε με U παριστάνουμε τη διεύθυνση κατά την οποία κινείται η μπάλα, με Β το κέντρο της μπάλας λίγο πριν φύγει από τα χέρια του μπασκετμπολίστα, με θ τη γωνία βολής της μπάλας, με Α το κέντρο του στεφανιού του καλαθιού, με την εσωτερική διάμετρο του στεφανιού, με φ τη γωνία (ως προς την οριζόντια διεύθυνση) με την οποία η μπάλα μπαίνει στο καλάθι, με
την εσωτερική διάμετρο του στεφανιού, με φ τη γωνία (ως προς την οριζόντια διεύθυνση) με την οποία η μπάλα μπαίνει στο καλάθι, με  το ύψος του στεφανιού από το πάτωμα, με δ (περίπου ίσο με
το ύψος του στεφανιού από το πάτωμα, με δ (περίπου ίσο με ) τη διάμετρο της μπάλας, με h τη διαφορά υψομέτρου ανάμεσα στο σημείο Β και το επίπεδο του καλαθιού, με
) τη διάμετρο της μπάλας, με h τη διαφορά υψομέτρου ανάμεσα στο σημείο Β και το επίπεδο του καλαθιού, με  την απόσταση του κέντρου του στεφανιού και του κέντρου της μπάλας την στιγμή που αυτή φτάνει στο στεφάνι, με L την οριζόντια απόσταση του κέντρου της μπάλας (την στιγμή που φεύγει από τα χέρια του μπασκετμπολίστα) και του κέντρου του στεφανιού, με V την αρχική ταχύτητα της μπάλας και
την απόσταση του κέντρου του στεφανιού και του κέντρου της μπάλας την στιγμή που αυτή φτάνει στο στεφάνι, με L την οριζόντια απόσταση του κέντρου της μπάλας (την στιγμή που φεύγει από τα χέρια του μπασκετμπολίστα) και του κέντρου του στεφανιού, με V την αρχική ταχύτητα της μπάλας και 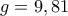
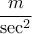 την επιτάχυνση της βαρύτητας.
την επιτάχυνση της βαρύτητας.
[attachment=0]ΜΠΑΣΚΕΤ [σχήμα].doc[/attachment]
Για να μπορέσει η μπάλα να περάσει μέσα στο στεφάνι, χωρίς να το αγγίξει, πρέπει
H συνθήκη αυτή έχει νόημα όταν , γιατί αν
, γιατί αν  η μπάλα θα χτυπήσει οπωσδήποτε στο χείλος του στεφανιού (ιδιαίτατα όταν η ταχύτητα της μπάλας είναι αρκετά μεγάλη τη στιγμή που χτυπά στο χείλος). Αν αυξήσουμε τη γωνία φ, αυξάνουμε τις πιθανότητές να "πετύχουμε" καλάθι. Μια "πολύ καλή" γωνία φ θεωρείται αυτή των
η μπάλα θα χτυπήσει οπωσδήποτε στο χείλος του στεφανιού (ιδιαίτατα όταν η ταχύτητα της μπάλας είναι αρκετά μεγάλη τη στιγμή που χτυπά στο χείλος). Αν αυξήσουμε τη γωνία φ, αυξάνουμε τις πιθανότητές να "πετύχουμε" καλάθι. Μια "πολύ καλή" γωνία φ θεωρείται αυτή των  .
.
Είναι φανερό ότι η γωνία φ αυξάνει όσο μεγαλύτερη γίνεται η γωνία θ. Αν προσπαθήσετε να σουτάρετε υπό μια μεγάλη γωνία θ (π.χ.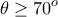 ) και από σχετικά μεγάλη απόσταση είναι μάλλον δύσκολο να πετύχετε καλάθι. Ορισμένες φορές μάλλιστα είναι δύσκολο να φτάσει η μπάλα στο στεφάνι. Όταν μερικές φορές οι παίκτες σουτάρουν από μακριά, αναγκάζονται να το κάνουν λόγω του ύψους και των μακριών χεριών των αντιπάλων.
) και από σχετικά μεγάλη απόσταση είναι μάλλον δύσκολο να πετύχετε καλάθι. Ορισμένες φορές μάλλιστα είναι δύσκολο να φτάσει η μπάλα στο στεφάνι. Όταν μερικές φορές οι παίκτες σουτάρουν από μακριά, αναγκάζονται να το κάνουν λόγω του ύψους και των μακριών χεριών των αντιπάλων.
Οι εξισώσεις που περιγράφουν την κίνηση του κέντρου της μπάλας είναι

Από τις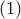 παίρνουμε
παίρνουμε
 ...........................
........................... 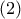
Από την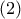 έπεται πως ένας παίχτης που απέχει δεδομένη απόσταση από τη μπασκέτα μπορεί να πετύχει ένα καλό σουτ με την ελάχιστη ταχύτητα – και, κατά συνέπεια, με την ελάχιστη κατανάλωση ενέργειας – όταν
έπεται πως ένας παίχτης που απέχει δεδομένη απόσταση από τη μπασκέτα μπορεί να πετύχει ένα καλό σουτ με την ελάχιστη ταχύτητα – και, κατά συνέπεια, με την ελάχιστη κατανάλωση ενέργειας – όταν 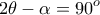 . Άρα η βέλτιστη γωνία βολής είναι
. Άρα η βέλτιστη γωνία βολής είναι
 .................
................. 
Η γωνία α εξαρτάται από το L. Στην περίπτωση μακρινού σουτ , η γωνία αυτή είναι πολύ μικρή και, σύμφωνα με την εξίσωση
, η γωνία αυτή είναι πολύ μικρή και, σύμφωνα με την εξίσωση  , η βέλτιστη γωνία βολής ισούται περίπου με
, η βέλτιστη γωνία βολής ισούται περίπου με  (ή ίσως κατά λίγες μοίρες μικρότερη).
(ή ίσως κατά λίγες μοίρες μικρότερη).
Ας ελέγξουμε αυτό το συμπέρασμα, υποθέτοντας ότι η μπάλα βρίσκεται σε ύψος 2 στην αρχική φάση της βολής (που είναι συνήθης περίπτωση εφόσον δεν είστε γίγαντας και σουτάρετε χωρίς να πηδάτε). Τότε
στην αρχική φάση της βολής (που είναι συνήθης περίπτωση εφόσον δεν είστε γίγαντας και σουτάρετε χωρίς να πηδάτε). Τότε 
 . Λαμβάνοντας ως απόσταση
. Λαμβάνοντας ως απόσταση 
 προκύπτει ότι
προκύπτει ότι 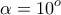 , δηλ.
, δηλ.  . Αντικαθιστώντας το αποτέλεσμα αυτό στην
. Αντικαθιστώντας το αποτέλεσμα αυτό στην  , υπολογίζουμε ότι η αρχική ταχύτητα της μπάλας θα έπρεπε (στην περίπτωσή μας) να ισούται με
, υπολογίζουμε ότι η αρχική ταχύτητα της μπάλας θα έπρεπε (στην περίπτωσή μας) να ισούται με 

Είναι ενδιαφέρον πως όταν η γωνία βολής είναι η βέλτιστη, η αρχική ταχύτητα εκτόξευσης της μπάλας είναι η ελάχιστη. Πρόκειται για μια ωραία ανακάλυψη. Αλλά η έννοια της βέλτιστης γωνίας έχει το πλεονέκτημα ότι μας οδηγεί σε ένα εκπληκτικό φαινόμενο: το μήκος του σουτ σχεδόν δεν εξαρτάται από μικρές αποκλίσεις της γωνίας βολής από τη βέλτιστη τιμή!! Το αποτέλεσμα αυτό είναι ιδιαίτερα χρήσιμο επειδή δυστυχώς (ή ευτυχώς) δεν είμαστε ρομπότ – διαπράττουμε σφάλματα και όχι μόνο κατά τη διάρκεια του μπάσκετ.
Η αντίσταση του αέρα
Σε όλους τους υπολογισμούς μας αγνοήσαμε την αντίσταση του αέρα. Όλοι, όμως, γνωρίζουμε πόσο σημαντικός είναι αυτός ο παράγοντας σε πολλά φυσικά φαινόμενα. Για παράδειγμα, η σφαίρα ενός τουφεκιού θα διένυε δεκαπλάσια απόσταση εάν δεν υπήρχε η ατμόσφαιρα. Η αντίσταση του αέρα εξαρτάται από το σχήμα του κινούμενου σώματος (σκεφτείτε τα αεροδυναμικά σχήματα των αεροπλάνων και των αγωνιστικών αυτοκινήτων), από τη μέγιστη διατομή κάθετα προς τη διεύθυνση κίνησης (γι' αυτό ένας μοτοσικλετιστής σκύβει μπροστά όταν τρέχει σε αγώνες), και ιδιαίτερα από την ταχύτητα του σώματος. Πιθανότατα έχετε προσέξει ότι ο αέρας αλλάζει την τροχιά της μπάλας του τένις, της μπάλας του ποδοσφαίρου, κ.ο.κ. Η μπάλα του μπάσκετ επηρεάζεται από τον αέρα σε μικρότερο βαθμό, κυρίως επειδή η κίνησή της είναι πολύ πιο αργή. Μια μπάλα αποκτά μεγαλύτερη αρχική ταχύτητα όταν τη χτυπήσουμε με μια ρακέτα ή την κλωτσήσουμε, παρά όταν τη σπρώξουμε με τα δάκτυλα. Οι μπάλες του τένις κινούνται με ταχύτητες έως
 , ενώ μια μπάλα του μπάσκετ συνήθως δεν κινείται ταχύτερα από 10
, ενώ μια μπάλα του μπάσκετ συνήθως δεν κινείται ταχύτερα από 10  .
.
Για να συμπεριλάβουμε την αντίσταση του αέρα στα σουτ του μπάσκετ θα χρειαζόταν να προσφύγουμε σε διαφορικές εξισώσεις.
Λίγη ιστορία
Το 1891, στο Σπρίγκφιλντ της Μασαχουσέτης, "γεννήθηκε" από τον Τζέϊμς Νέϊσμιθ το μπάσκετ, με καλάθι ένα πραγματικό καλάθι για ροδάκινα.
Το 1977 ο Τεντ Μάρτιν πέτυχε 2.036 καλαθιές σε ισάριθμες βολές.
Το 1978 ο Φρεντ Νιούμαν πέτυχε 88 συνεχείς καλαθιές με κλειστά μάτια !!»
Με εκτίμηση
Γιάννης Κερασαρίδης
«ΟΠΟΙΟΣ ΞΕΡΕΙ ΚΑΛΑ ΜΑΘΗΜΑΤΙΚΑ ΞΕΡΕΙ ΚΑΙ ΚΑΛΟ...ΜΠΑΣΚΕΤ;»
Προλεγόμενα Χθες με επισκέφθηκε ένας καλός φίλος Γυμναστής. Ανάμεσα στα άλλα μου θύμισε ένα παλιό σημείωμα που είχα δημοσιεύσει με θέμα το μπάσκετ. Με αφορμή αυτή την υπενθύμιση, σκέφθηκα να αναδημοσιεύσω εκείνο το σημείωμα. Σας το παρουσιάζω όπως είχε δημοσιευθεί τότε. Ο «Γυμναστής» εκείνου του σημειώματος είναι ο φίλος που με επισκέφθηκε.
Το δημοσίευμα εκείνο
«Προ καιρού ένας καλός φίλος Γυμναστής, που ασχολείται με τα σπορ με τόση επιμέλεια, όση και ο ζήλος του Gauss για τα Μαθηματικά, μας ξάφνιασε όταν μας είπε πως, σε ένα σεμινάριο που έλαβε μέρος, άκουσε ότι τα Μαθηματικά χρησιμεύουν για την μελέτη ενός από τα πιο δημοφιλή αθλήματα, του μπάσκετ. Ψάξαμε τη σχετική βιβλιογραφία. Από το θησαυρό πληροφοριών που βγήκε στην επιφάνεια διαλέξαμε αυτό που βρήκαμε στο έγκυρο επιστημονικό περιοδικό (βιβλιοθήκης), το "QUANTUM" (εκδόσεις "Κάτοπτρο"), με τίτλο: "Άλματα και καλαθιές, κινηματική στο γήπεδο του μπάσκετ" του Roman Vinokur (τόμος 2, τεύχος 5). Σας παρουσιάζουμε τα κυριότερα σημεία του.
Στο σχήμα που βλέπετε με U παριστάνουμε τη διεύθυνση κατά την οποία κινείται η μπάλα, με Β το κέντρο της μπάλας λίγο πριν φύγει από τα χέρια του μπασκετμπολίστα, με θ τη γωνία βολής της μπάλας, με Α το κέντρο του στεφανιού του καλαθιού, με
 την εσωτερική διάμετρο του στεφανιού, με φ τη γωνία (ως προς την οριζόντια διεύθυνση) με την οποία η μπάλα μπαίνει στο καλάθι, με
την εσωτερική διάμετρο του στεφανιού, με φ τη γωνία (ως προς την οριζόντια διεύθυνση) με την οποία η μπάλα μπαίνει στο καλάθι, με  το ύψος του στεφανιού από το πάτωμα, με δ (περίπου ίσο με
το ύψος του στεφανιού από το πάτωμα, με δ (περίπου ίσο με ) τη διάμετρο της μπάλας, με h τη διαφορά υψομέτρου ανάμεσα στο σημείο Β και το επίπεδο του καλαθιού, με
) τη διάμετρο της μπάλας, με h τη διαφορά υψομέτρου ανάμεσα στο σημείο Β και το επίπεδο του καλαθιού, με  την απόσταση του κέντρου του στεφανιού και του κέντρου της μπάλας την στιγμή που αυτή φτάνει στο στεφάνι, με L την οριζόντια απόσταση του κέντρου της μπάλας (την στιγμή που φεύγει από τα χέρια του μπασκετμπολίστα) και του κέντρου του στεφανιού, με V την αρχική ταχύτητα της μπάλας και
την απόσταση του κέντρου του στεφανιού και του κέντρου της μπάλας την στιγμή που αυτή φτάνει στο στεφάνι, με L την οριζόντια απόσταση του κέντρου της μπάλας (την στιγμή που φεύγει από τα χέρια του μπασκετμπολίστα) και του κέντρου του στεφανιού, με V την αρχική ταχύτητα της μπάλας και 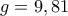
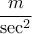 την επιτάχυνση της βαρύτητας.
την επιτάχυνση της βαρύτητας. [attachment=0]ΜΠΑΣΚΕΤ [σχήμα].doc[/attachment]
Για να μπορέσει η μπάλα να περάσει μέσα στο στεφάνι, χωρίς να το αγγίξει, πρέπει

H συνθήκη αυτή έχει νόημα όταν
 , γιατί αν
, γιατί αν  η μπάλα θα χτυπήσει οπωσδήποτε στο χείλος του στεφανιού (ιδιαίτατα όταν η ταχύτητα της μπάλας είναι αρκετά μεγάλη τη στιγμή που χτυπά στο χείλος). Αν αυξήσουμε τη γωνία φ, αυξάνουμε τις πιθανότητές να "πετύχουμε" καλάθι. Μια "πολύ καλή" γωνία φ θεωρείται αυτή των
η μπάλα θα χτυπήσει οπωσδήποτε στο χείλος του στεφανιού (ιδιαίτατα όταν η ταχύτητα της μπάλας είναι αρκετά μεγάλη τη στιγμή που χτυπά στο χείλος). Αν αυξήσουμε τη γωνία φ, αυξάνουμε τις πιθανότητές να "πετύχουμε" καλάθι. Μια "πολύ καλή" γωνία φ θεωρείται αυτή των  .
.Είναι φανερό ότι η γωνία φ αυξάνει όσο μεγαλύτερη γίνεται η γωνία θ. Αν προσπαθήσετε να σουτάρετε υπό μια μεγάλη γωνία θ (π.χ.
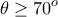 ) και από σχετικά μεγάλη απόσταση είναι μάλλον δύσκολο να πετύχετε καλάθι. Ορισμένες φορές μάλλιστα είναι δύσκολο να φτάσει η μπάλα στο στεφάνι. Όταν μερικές φορές οι παίκτες σουτάρουν από μακριά, αναγκάζονται να το κάνουν λόγω του ύψους και των μακριών χεριών των αντιπάλων.
) και από σχετικά μεγάλη απόσταση είναι μάλλον δύσκολο να πετύχετε καλάθι. Ορισμένες φορές μάλλιστα είναι δύσκολο να φτάσει η μπάλα στο στεφάνι. Όταν μερικές φορές οι παίκτες σουτάρουν από μακριά, αναγκάζονται να το κάνουν λόγω του ύψους και των μακριών χεριών των αντιπάλων. Οι εξισώσεις που περιγράφουν την κίνηση του κέντρου της μπάλας είναι

Από τις
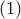 παίρνουμε
παίρνουμε ...........................
........................... 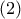
Από την
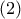 έπεται πως ένας παίχτης που απέχει δεδομένη απόσταση από τη μπασκέτα μπορεί να πετύχει ένα καλό σουτ με την ελάχιστη ταχύτητα – και, κατά συνέπεια, με την ελάχιστη κατανάλωση ενέργειας – όταν
έπεται πως ένας παίχτης που απέχει δεδομένη απόσταση από τη μπασκέτα μπορεί να πετύχει ένα καλό σουτ με την ελάχιστη ταχύτητα – και, κατά συνέπεια, με την ελάχιστη κατανάλωση ενέργειας – όταν 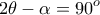 . Άρα η βέλτιστη γωνία βολής είναι
. Άρα η βέλτιστη γωνία βολής είναι .................
................. 
Η γωνία α εξαρτάται από το L. Στην περίπτωση μακρινού σουτ
 , η γωνία αυτή είναι πολύ μικρή και, σύμφωνα με την εξίσωση
, η γωνία αυτή είναι πολύ μικρή και, σύμφωνα με την εξίσωση  , η βέλτιστη γωνία βολής ισούται περίπου με
, η βέλτιστη γωνία βολής ισούται περίπου με  (ή ίσως κατά λίγες μοίρες μικρότερη).
(ή ίσως κατά λίγες μοίρες μικρότερη).Ας ελέγξουμε αυτό το συμπέρασμα, υποθέτοντας ότι η μπάλα βρίσκεται σε ύψος 2
 στην αρχική φάση της βολής (που είναι συνήθης περίπτωση εφόσον δεν είστε γίγαντας και σουτάρετε χωρίς να πηδάτε). Τότε
στην αρχική φάση της βολής (που είναι συνήθης περίπτωση εφόσον δεν είστε γίγαντας και σουτάρετε χωρίς να πηδάτε). Τότε 
 . Λαμβάνοντας ως απόσταση
. Λαμβάνοντας ως απόσταση 
 προκύπτει ότι
προκύπτει ότι 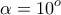 , δηλ.
, δηλ.  . Αντικαθιστώντας το αποτέλεσμα αυτό στην
. Αντικαθιστώντας το αποτέλεσμα αυτό στην 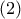 , υπολογίζουμε ότι η αρχική ταχύτητα της μπάλας θα έπρεπε (στην περίπτωσή μας) να ισούται με
, υπολογίζουμε ότι η αρχική ταχύτητα της μπάλας θα έπρεπε (στην περίπτωσή μας) να ισούται με 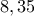

Είναι ενδιαφέρον πως όταν η γωνία βολής είναι η βέλτιστη, η αρχική ταχύτητα εκτόξευσης της μπάλας είναι η ελάχιστη. Πρόκειται για μια ωραία ανακάλυψη. Αλλά η έννοια της βέλτιστης γωνίας έχει το πλεονέκτημα ότι μας οδηγεί σε ένα εκπληκτικό φαινόμενο: το μήκος του σουτ σχεδόν δεν εξαρτάται από μικρές αποκλίσεις της γωνίας βολής από τη βέλτιστη τιμή!! Το αποτέλεσμα αυτό είναι ιδιαίτερα χρήσιμο επειδή δυστυχώς (ή ευτυχώς) δεν είμαστε ρομπότ – διαπράττουμε σφάλματα και όχι μόνο κατά τη διάρκεια του μπάσκετ.
Η αντίσταση του αέρα
Σε όλους τους υπολογισμούς μας αγνοήσαμε την αντίσταση του αέρα. Όλοι, όμως, γνωρίζουμε πόσο σημαντικός είναι αυτός ο παράγοντας σε πολλά φυσικά φαινόμενα. Για παράδειγμα, η σφαίρα ενός τουφεκιού θα διένυε δεκαπλάσια απόσταση εάν δεν υπήρχε η ατμόσφαιρα. Η αντίσταση του αέρα εξαρτάται από το σχήμα του κινούμενου σώματος (σκεφτείτε τα αεροδυναμικά σχήματα των αεροπλάνων και των αγωνιστικών αυτοκινήτων), από τη μέγιστη διατομή κάθετα προς τη διεύθυνση κίνησης (γι' αυτό ένας μοτοσικλετιστής σκύβει μπροστά όταν τρέχει σε αγώνες), και ιδιαίτερα από την ταχύτητα του σώματος. Πιθανότατα έχετε προσέξει ότι ο αέρας αλλάζει την τροχιά της μπάλας του τένις, της μπάλας του ποδοσφαίρου, κ.ο.κ. Η μπάλα του μπάσκετ επηρεάζεται από τον αέρα σε μικρότερο βαθμό, κυρίως επειδή η κίνησή της είναι πολύ πιο αργή. Μια μπάλα αποκτά μεγαλύτερη αρχική ταχύτητα όταν τη χτυπήσουμε με μια ρακέτα ή την κλωτσήσουμε, παρά όταν τη σπρώξουμε με τα δάκτυλα. Οι μπάλες του τένις κινούνται με ταχύτητες έως

 , ενώ μια μπάλα του μπάσκετ συνήθως δεν κινείται ταχύτερα από 10
, ενώ μια μπάλα του μπάσκετ συνήθως δεν κινείται ταχύτερα από 10  .
.Για να συμπεριλάβουμε την αντίσταση του αέρα στα σουτ του μπάσκετ θα χρειαζόταν να προσφύγουμε σε διαφορικές εξισώσεις.
Λίγη ιστορία
Το 1891, στο Σπρίγκφιλντ της Μασαχουσέτης, "γεννήθηκε" από τον Τζέϊμς Νέϊσμιθ το μπάσκετ, με καλάθι ένα πραγματικό καλάθι για ροδάκινα.
Το 1977 ο Τεντ Μάρτιν πέτυχε 2.036 καλαθιές σε ισάριθμες βολές.
Το 1978 ο Φρεντ Νιούμαν πέτυχε 88 συνεχείς καλαθιές με κλειστά μάτια !!»
Με εκτίμηση
Γιάννης Κερασαρίδης
- Συνημμένα
-
- ΜΠΑΣΚΕΤ [σχήμα].doc
- (34 KiB) Μεταφορτώθηκε 42 φορές
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
28ο ΣΗΜΕΙΩΜΑ
«ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ...BASEBALL»,
Προλεγόμενα Μετά το 27ο σημείωμα, σκεφθήκαμε να αναδημοσιεύσουμε άλλο ένα "αθλητικό" δημοσίευμά μας, με θέμα το baseball. Σας το παραθέτουμε:
«Ένα φρεσκάρισμα της μνήμης των μαθητών: Η ακολουθία των αριθμών 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,... είναι από τις πιο διάσημες και φέρει το όνομα του Ιταλού μαθηματικού Fibonacci ή Leonardo da Pisa (1170 – 1250 μΧ.). Παρατηρήστε ότι, αν σε κάθε όρο προσθέσουμε τον προηγούμενό του, παίρνουμε τον επόμενο. Έτσι 1,
Εδώ πρέπει να αναφέρουμε ότι, αν αρχίσουμε και διαιρούμε κάθε όρο της ακολουθίας Fibonacci (από τον δεύτερο και μετά), με τον πρηγούμενό του, θα δια-πιστώσουμε πως, το πηλίκο που θα προκύπτει κάθε φορά, θα πλησιάζει προς τον αριθμό . Αυτός ο αριθμός είναι γνωστός ως Χρυσή Αναλογία, θεωρείται συντελεστής ομορφιάς (αισθητικής απόλαυσης), τον συναντάμε στη Φύση, τον χρησιμοποίησαν μεγάλοι ζωγράφοι (Λεονάρντο ντα Βίντσι,...), γλύπτες (Φειδίας, Μύρων,...), αρχιτέκτονες (Φειδίας, Ικτίνος,...) και, τώρα, οι... κριτές στους αγώνες baseball.
. Αυτός ο αριθμός είναι γνωστός ως Χρυσή Αναλογία, θεωρείται συντελεστής ομορφιάς (αισθητικής απόλαυσης), τον συναντάμε στη Φύση, τον χρησιμοποίησαν μεγάλοι ζωγράφοι (Λεονάρντο ντα Βίντσι,...), γλύπτες (Φειδίας, Μύρων,...), αρχιτέκτονες (Φειδίας, Ικτίνος,...) και, τώρα, οι... κριτές στους αγώνες baseball.
και τώρα το baseball
Τι είναι το baseball: Αθλητικό παιχνίδι για 2 ομάδες από 9 παίκτες. Το γήπεδο του baseball είναι σκληρό και έχει διαστάσεις
 . Στο εσωτερικό του σημειώνεται ένα τετράγωνο με πλευρά
. Στο εσωτερικό του σημειώνεται ένα τετράγωνο με πλευρά 
 . Στην κάθε γωνία αυτού του τετραγώνου, υπάρχει ένα μικρό τετραγωνάκι, γνωστό σαν "εστία". Η μία ομάδα λέγεται "αμυντική" και η άλλη "επιθετική" [κλικ στο: ΕΙΚΟΝΑ ΓΗΠΕΔΟΥ BASEBALL]. Ο αγώνας διεξάγεται με 9 "αμυντικούς" και ένα "επιθετικό" (τον "μπάτσερ") που με το ρόπαλο στα χέρια χτυπά τη μπάλα και τη στέλνει μακριά, ώστε να δυσκολεύονται οι "αμυντικοί" να την πιάνουν αμέσως. Ο "μπάτσερ" παίρνει θέση στo κέντρο του τετραγώνου Απέναντί του, σε απόσταση
. Στην κάθε γωνία αυτού του τετραγώνου, υπάρχει ένα μικρό τετραγωνάκι, γνωστό σαν "εστία". Η μία ομάδα λέγεται "αμυντική" και η άλλη "επιθετική" [κλικ στο: ΕΙΚΟΝΑ ΓΗΠΕΔΟΥ BASEBALL]. Ο αγώνας διεξάγεται με 9 "αμυντικούς" και ένα "επιθετικό" (τον "μπάτσερ") που με το ρόπαλο στα χέρια χτυπά τη μπάλα και τη στέλνει μακριά, ώστε να δυσκολεύονται οι "αμυντικοί" να την πιάνουν αμέσως. Ο "μπάτσερ" παίρνει θέση στo κέντρο του τετραγώνου Απέναντί του, σε απόσταση 
 , παίρνει θέση ο υπ’ αριθ. 1 "αμυντικός" (ο "ρίπτης" ή "πίτσερ"), ενώ δίπλα και λίγο πίσω του "μπάτσερ" βρίσκεται ο υπ’ αριθ. 2 "αμυντικός", οι υπ’ αριθ 3,4,5,6 παίρνουν θέσεις στο μέσα μέρος του γηπέδου και οι άλλοι 7,8, 9 σκορπίζονται στον εξωτερικό χώρο, υπολογίζοντας να πιάσουν τη μπάλα στον αέρα, όταν θα πετύχει να τη στείλει ως εκεί ο "μπάτσερ".
, παίρνει θέση ο υπ’ αριθ. 1 "αμυντικός" (ο "ρίπτης" ή "πίτσερ"), ενώ δίπλα και λίγο πίσω του "μπάτσερ" βρίσκεται ο υπ’ αριθ. 2 "αμυντικός", οι υπ’ αριθ 3,4,5,6 παίρνουν θέσεις στο μέσα μέρος του γηπέδου και οι άλλοι 7,8, 9 σκορπίζονται στον εξωτερικό χώρο, υπολογίζοντας να πιάσουν τη μπάλα στον αέρα, όταν θα πετύχει να τη στείλει ως εκεί ο "μπάτσερ".
Το παιχνίδι αρχίζει με την ρίψη της μπάλας, με το χέρι, από τον "πίτσερ" προς τον "μπάτσερ". Η μπάλα δεν πρέπει να πεταχτεί χαμηλότερα από το ύψος του γόνατος ή ψηλότερα από το ύψος του ώμου και, επίσης, πρέπει να πάει σε ίσια βολή. Ο "μπάτσερ" προσπαθεί να χτυπήσει τη μπάλα. Κι αν το πετύχει και τη στείλει μακριά, αφήνει το ρόπαλο και τρέχει να φτάσει στην "εστία" της πρώτης γωνίας κι αν νομίζει ότι προλαβαίνει, πριν οι αντίπαλοί του πιάσουν τη μπάλα και του κόψουν το δρόμο στη μέση, τρέχει και στην άλλη εστία. Αν προλάβει να γυρίσει όλες τις εστίες (home run) κερδίζει ένα βαθμό. Αν πριν ακουμπήσει το πόδι του στο άσπρο σημάδι της εστίας, ο ευρισκόμενος εκεί αντίπαλός του προλάβει και πιάσει τη μπάλα που, κάποιος συμπαίκτης του, του την γύρισε από μακριά, τότε ο "μπάτσερ" που έτρεχε "καίγεται", δηλ. αποκλείεται και η αμυνόμενη ομάδα κερδίζει βαθμό. Τη θέση του παίρνει άλλος "επιθετικός" και ο αγώνας συνεχίζεται. Συμβαίνει, όμως, μερικές φορές ο "μπάτσερ" να αστοχήσει, να μη χτυπήσει τη μπάλα που πετάει ο "πίτσερ". Αν αυτό γίνει τρεις φορές και η μπάλα περάσει το σημείο και την πιάσει ο υπ’ αριθ 2 "αμυντικός", τότε ο "μπάτσερ" καίγεται και αποκλείεται, η άλλη ομάδα παίρνει βαθμό και νέος παίκτης παίρνει τη θέση του προηγούμενου "μπάτσερ". Αν βγουν τρεις παίχτες της ομάδας τελειώνει το "game".
Στην περίπτωση που "αμυνόμενος" παίκτης πιάσει τη μπάλα στον αέρα, ο "μπάτσερ" καίγεται και αντικαθίσταται. Το σπουδαιότερο ρόλο στο παιχνίδι έχει ο "πίτσερ". Εκτός του ότι έχει τις δυνατότητες να πετάει τόσο δυνατά τη μπάλα, ώστε αυτή να αναπτύσσει ταχύτητα...πάνω από 100 km, οπότε συνήθως δεν προλαβαίνει ο "μπάτσερ" να αποκρούσει, μερικές φορές, προσποι-ούμενος ότι στέλνει τη μπάλα με όλη τη δύναμή του, τη στέλνει με μικρότερη ταχύτητα και ξεγε-λά τον "μπάτσερ", που κάνει την κίνηση και βρίσκοντας κενό, δεν προλαβαίνει να χτυπήσει τη μπάλα, την οποία πιάνει ο υπ’ αριθ. 2 "αμυντικός"
Ο Fibonacci, o Bill James και η...μαθηματικοποίηση του baseball
Τι "μετρά", στην αξιολόγηση της απόδοσης, στο baseball: Τα στοιχεία που "μετρούν" στην αξιολόγηση της απόδοσης στους αγώνες baseball είναι α) οι νίκες, β) το ποσοστό των νι-κών, δηλ. το πηλίκο των νικών προς το άθροισμα των νικών και των ηττών, γ) η διαφορά νικών-ηττών.
Ο τύπος του Bill James: Ο Bill James είναι ένας άνθρωπος με μεγάλο πάθος για το baseball. Τον απασχόλησε ένα πρόβλημα: αν έχουμε δύο "πίτσερς" ("ρίπτες" της μπάλας) και θέ-λουμε να τους αξιολογήσουμε, δηλ. να τους συγκρίνουμε ως προς τις επιδόσεις τους, ποια είναι η προσφορότερη μέθοδος; Έκατσε, λοιπόν, και μελέτησε στατιστικά τις νίκες και τις ήττες πολλών "πίτσερς" του baseball, στη διάρκεια της ως τότε καριέρας τους. Το αποτέλεσμα αυτής της μελέ-της του, ήταν να γράψει ένα βιβλίο με τίτλο «The politics of glory: how baseball’s Hall of Fame really works?»
Στο βιβλίο αυτό, ο Bill James, καθιερώνει μια νέα κλίμακα βαθμολογίας που την κάθε μονάδα της την ονομάζει "Fibonacci βαθμό νίκης". Για να δούμε, για πιο λόγο η νέα κλίμακα βαθμολογίας ονομάσθηκε έτσι, θα πρέπει πρώτα να γνωρίσουμε τον μαθηματικό τύπο που επινόησε ο James. Αν παραστήσουμε με W το πλήθος των νικών, με L το πλήθος των ηττών και με το πλήθος των "Fibonacci βαθμών νίκης" που αντιστοιχούν στον κάθε παίκτη, τότε ισχύει ο τύπος:
το πλήθος των "Fibonacci βαθμών νίκης" που αντιστοιχούν στον κάθε παίκτη, τότε ισχύει ο τύπος:

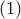
Ένα παράδειγμα: Θεωρούμε δύο "πίτσερς", τον Α και τον Β. Ο Α έχει 200 νίκες και 90 ήττες, ενώ ο Β έχει 250 νίκες και 180 ήττες. Παρατηρούμε ότι ο Α έχει 50 νίκες λιγότερες από τον Β, όμως έχει 90 ήττες λιγότερες από τον Β. Αν με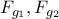 , παραστήσουμε τους "Fibonacci βαθμούς νίκης" των Α,Β αντίστοιχα, και αντικαταστήσουμε τις αντίστοιχες τιμές του καθενός στον τύπο
, παραστήσουμε τους "Fibonacci βαθμούς νίκης" των Α,Β αντίστοιχα, και αντικαταστήσουμε τις αντίστοιχες τιμές του καθενός στον τύπο  , τότε παίρνουμε
, τότε παίρνουμε  "Fibonacci βαθμούς νίκης" και
"Fibonacci βαθμούς νίκης" και  "Fibonacci βαθμούς νίκης". Από τη σύγκριση των αποτελεσμάτων αυτών, βγαίνει το συμπέρασμα, πως ο "ρίπτης" Α είναι καλύτερος από τον "ρίπτη" Β. Να, λοιπόν, μια ακόμη προσφορά των Μαθηματικών στον αθλητισμό.
"Fibonacci βαθμούς νίκης". Από τη σύγκριση των αποτελεσμάτων αυτών, βγαίνει το συμπέρασμα, πως ο "ρίπτης" Α είναι καλύτερος από τον "ρίπτη" Β. Να, λοιπόν, μια ακόμη προσφορά των Μαθηματικών στον αθλητισμό.
Ασκηση: Ο Sandy Coufax είχε 165 νίκες και 87 ήττες και ο Jim Bunnig 224 νίκες και 184 ήττες. Ποιος είναι καλύτερος;
Σχέση ανάμεσα στο baseball, την ακολουθία Fibonacci και τη Χρυσή Αναλογία
Στο κρίσιμο σημείο, όπου οι νίκες συμπίπτουν με τους "Fibonacci βαθμούς νίκης", έχουμε τελικά από την :
:

Να, λοιπόν, η Χρυσή Αναλογία και η σχέση της με το baseball.
και η σχέση της με το baseball.
Βιβλιογραφία
Το υλικό, για να γραφτεί αυτή η εργασία, το δανειστήκαμε από: 1) Μπάμπη Τουμάση «Χρυσή Τομή – Fibonacci – Λαγοί και Λουλούδια», 2) QUANTUM, 3) Ιστορία του Ελληνικού Έθνους, 4) Πάπυρος-Larousse-Britannica»
Υ.Γ. 1 Στο επόμενο σημείωμα θα δούμε αν, για να παίξουμε καλό μπιλιάρδο, χρειάζεται να ξέρουμε Μαθηματικά
Υ.Γ. 2 Με το 30ο σημείωμα θα κλείσουμε το θέμα «ΓΙΑ ΠΟΙΟ ΛΟΓΟ ΔΙΔΑΣΚΟΥΜΕ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΑ ΠΑΙΔΙΑ;»
με εκτίμηση
Γιάννης Κερασαρίδης
«ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΤΟ ...BASEBALL»,
Προλεγόμενα Μετά το 27ο σημείωμα, σκεφθήκαμε να αναδημοσιεύσουμε άλλο ένα "αθλητικό" δημοσίευμά μας, με θέμα το baseball. Σας το παραθέτουμε:
«Ένα φρεσκάρισμα της μνήμης των μαθητών: Η ακολουθία των αριθμών 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,... είναι από τις πιο διάσημες και φέρει το όνομα του Ιταλού μαθηματικού Fibonacci ή Leonardo da Pisa (1170 – 1250 μΧ.). Παρατηρήστε ότι, αν σε κάθε όρο προσθέσουμε τον προηγούμενό του, παίρνουμε τον επόμενο. Έτσι 1,

Εδώ πρέπει να αναφέρουμε ότι, αν αρχίσουμε και διαιρούμε κάθε όρο της ακολουθίας Fibonacci (από τον δεύτερο και μετά), με τον πρηγούμενό του, θα δια-πιστώσουμε πως, το πηλίκο που θα προκύπτει κάθε φορά, θα πλησιάζει προς τον αριθμό
 . Αυτός ο αριθμός είναι γνωστός ως Χρυσή Αναλογία, θεωρείται συντελεστής ομορφιάς (αισθητικής απόλαυσης), τον συναντάμε στη Φύση, τον χρησιμοποίησαν μεγάλοι ζωγράφοι (Λεονάρντο ντα Βίντσι,...), γλύπτες (Φειδίας, Μύρων,...), αρχιτέκτονες (Φειδίας, Ικτίνος,...) και, τώρα, οι... κριτές στους αγώνες baseball.
. Αυτός ο αριθμός είναι γνωστός ως Χρυσή Αναλογία, θεωρείται συντελεστής ομορφιάς (αισθητικής απόλαυσης), τον συναντάμε στη Φύση, τον χρησιμοποίησαν μεγάλοι ζωγράφοι (Λεονάρντο ντα Βίντσι,...), γλύπτες (Φειδίας, Μύρων,...), αρχιτέκτονες (Φειδίας, Ικτίνος,...) και, τώρα, οι... κριτές στους αγώνες baseball.και τώρα το baseball
Τι είναι το baseball: Αθλητικό παιχνίδι για 2 ομάδες από 9 παίκτες. Το γήπεδο του baseball είναι σκληρό και έχει διαστάσεις

 . Στο εσωτερικό του σημειώνεται ένα τετράγωνο με πλευρά
. Στο εσωτερικό του σημειώνεται ένα τετράγωνο με πλευρά 
 . Στην κάθε γωνία αυτού του τετραγώνου, υπάρχει ένα μικρό τετραγωνάκι, γνωστό σαν "εστία". Η μία ομάδα λέγεται "αμυντική" και η άλλη "επιθετική" [κλικ στο: ΕΙΚΟΝΑ ΓΗΠΕΔΟΥ BASEBALL]. Ο αγώνας διεξάγεται με 9 "αμυντικούς" και ένα "επιθετικό" (τον "μπάτσερ") που με το ρόπαλο στα χέρια χτυπά τη μπάλα και τη στέλνει μακριά, ώστε να δυσκολεύονται οι "αμυντικοί" να την πιάνουν αμέσως. Ο "μπάτσερ" παίρνει θέση στo κέντρο του τετραγώνου Απέναντί του, σε απόσταση
. Στην κάθε γωνία αυτού του τετραγώνου, υπάρχει ένα μικρό τετραγωνάκι, γνωστό σαν "εστία". Η μία ομάδα λέγεται "αμυντική" και η άλλη "επιθετική" [κλικ στο: ΕΙΚΟΝΑ ΓΗΠΕΔΟΥ BASEBALL]. Ο αγώνας διεξάγεται με 9 "αμυντικούς" και ένα "επιθετικό" (τον "μπάτσερ") που με το ρόπαλο στα χέρια χτυπά τη μπάλα και τη στέλνει μακριά, ώστε να δυσκολεύονται οι "αμυντικοί" να την πιάνουν αμέσως. Ο "μπάτσερ" παίρνει θέση στo κέντρο του τετραγώνου Απέναντί του, σε απόσταση 
 , παίρνει θέση ο υπ’ αριθ. 1 "αμυντικός" (ο "ρίπτης" ή "πίτσερ"), ενώ δίπλα και λίγο πίσω του "μπάτσερ" βρίσκεται ο υπ’ αριθ. 2 "αμυντικός", οι υπ’ αριθ 3,4,5,6 παίρνουν θέσεις στο μέσα μέρος του γηπέδου και οι άλλοι 7,8, 9 σκορπίζονται στον εξωτερικό χώρο, υπολογίζοντας να πιάσουν τη μπάλα στον αέρα, όταν θα πετύχει να τη στείλει ως εκεί ο "μπάτσερ".
, παίρνει θέση ο υπ’ αριθ. 1 "αμυντικός" (ο "ρίπτης" ή "πίτσερ"), ενώ δίπλα και λίγο πίσω του "μπάτσερ" βρίσκεται ο υπ’ αριθ. 2 "αμυντικός", οι υπ’ αριθ 3,4,5,6 παίρνουν θέσεις στο μέσα μέρος του γηπέδου και οι άλλοι 7,8, 9 σκορπίζονται στον εξωτερικό χώρο, υπολογίζοντας να πιάσουν τη μπάλα στον αέρα, όταν θα πετύχει να τη στείλει ως εκεί ο "μπάτσερ". Το παιχνίδι αρχίζει με την ρίψη της μπάλας, με το χέρι, από τον "πίτσερ" προς τον "μπάτσερ". Η μπάλα δεν πρέπει να πεταχτεί χαμηλότερα από το ύψος του γόνατος ή ψηλότερα από το ύψος του ώμου και, επίσης, πρέπει να πάει σε ίσια βολή. Ο "μπάτσερ" προσπαθεί να χτυπήσει τη μπάλα. Κι αν το πετύχει και τη στείλει μακριά, αφήνει το ρόπαλο και τρέχει να φτάσει στην "εστία" της πρώτης γωνίας κι αν νομίζει ότι προλαβαίνει, πριν οι αντίπαλοί του πιάσουν τη μπάλα και του κόψουν το δρόμο στη μέση, τρέχει και στην άλλη εστία. Αν προλάβει να γυρίσει όλες τις εστίες (home run) κερδίζει ένα βαθμό. Αν πριν ακουμπήσει το πόδι του στο άσπρο σημάδι της εστίας, ο ευρισκόμενος εκεί αντίπαλός του προλάβει και πιάσει τη μπάλα που, κάποιος συμπαίκτης του, του την γύρισε από μακριά, τότε ο "μπάτσερ" που έτρεχε "καίγεται", δηλ. αποκλείεται και η αμυνόμενη ομάδα κερδίζει βαθμό. Τη θέση του παίρνει άλλος "επιθετικός" και ο αγώνας συνεχίζεται. Συμβαίνει, όμως, μερικές φορές ο "μπάτσερ" να αστοχήσει, να μη χτυπήσει τη μπάλα που πετάει ο "πίτσερ". Αν αυτό γίνει τρεις φορές και η μπάλα περάσει το σημείο και την πιάσει ο υπ’ αριθ 2 "αμυντικός", τότε ο "μπάτσερ" καίγεται και αποκλείεται, η άλλη ομάδα παίρνει βαθμό και νέος παίκτης παίρνει τη θέση του προηγούμενου "μπάτσερ". Αν βγουν τρεις παίχτες της ομάδας τελειώνει το "game".
Στην περίπτωση που "αμυνόμενος" παίκτης πιάσει τη μπάλα στον αέρα, ο "μπάτσερ" καίγεται και αντικαθίσταται. Το σπουδαιότερο ρόλο στο παιχνίδι έχει ο "πίτσερ". Εκτός του ότι έχει τις δυνατότητες να πετάει τόσο δυνατά τη μπάλα, ώστε αυτή να αναπτύσσει ταχύτητα...πάνω από 100 km, οπότε συνήθως δεν προλαβαίνει ο "μπάτσερ" να αποκρούσει, μερικές φορές, προσποι-ούμενος ότι στέλνει τη μπάλα με όλη τη δύναμή του, τη στέλνει με μικρότερη ταχύτητα και ξεγε-λά τον "μπάτσερ", που κάνει την κίνηση και βρίσκοντας κενό, δεν προλαβαίνει να χτυπήσει τη μπάλα, την οποία πιάνει ο υπ’ αριθ. 2 "αμυντικός"
Ο Fibonacci, o Bill James και η...μαθηματικοποίηση του baseball
Τι "μετρά", στην αξιολόγηση της απόδοσης, στο baseball: Τα στοιχεία που "μετρούν" στην αξιολόγηση της απόδοσης στους αγώνες baseball είναι α) οι νίκες, β) το ποσοστό των νι-κών, δηλ. το πηλίκο των νικών προς το άθροισμα των νικών και των ηττών, γ) η διαφορά νικών-ηττών.
Ο τύπος του Bill James: Ο Bill James είναι ένας άνθρωπος με μεγάλο πάθος για το baseball. Τον απασχόλησε ένα πρόβλημα: αν έχουμε δύο "πίτσερς" ("ρίπτες" της μπάλας) και θέ-λουμε να τους αξιολογήσουμε, δηλ. να τους συγκρίνουμε ως προς τις επιδόσεις τους, ποια είναι η προσφορότερη μέθοδος; Έκατσε, λοιπόν, και μελέτησε στατιστικά τις νίκες και τις ήττες πολλών "πίτσερς" του baseball, στη διάρκεια της ως τότε καριέρας τους. Το αποτέλεσμα αυτής της μελέ-της του, ήταν να γράψει ένα βιβλίο με τίτλο «The politics of glory: how baseball’s Hall of Fame really works?»
Στο βιβλίο αυτό, ο Bill James, καθιερώνει μια νέα κλίμακα βαθμολογίας που την κάθε μονάδα της την ονομάζει "Fibonacci βαθμό νίκης". Για να δούμε, για πιο λόγο η νέα κλίμακα βαθμολογίας ονομάσθηκε έτσι, θα πρέπει πρώτα να γνωρίσουμε τον μαθηματικό τύπο που επινόησε ο James. Αν παραστήσουμε με W το πλήθος των νικών, με L το πλήθος των ηττών και με
 το πλήθος των "Fibonacci βαθμών νίκης" που αντιστοιχούν στον κάθε παίκτη, τότε ισχύει ο τύπος:
το πλήθος των "Fibonacci βαθμών νίκης" που αντιστοιχούν στον κάθε παίκτη, τότε ισχύει ο τύπος: 
Ένα παράδειγμα: Θεωρούμε δύο "πίτσερς", τον Α και τον Β. Ο Α έχει 200 νίκες και 90 ήττες, ενώ ο Β έχει 250 νίκες και 180 ήττες. Παρατηρούμε ότι ο Α έχει 50 νίκες λιγότερες από τον Β, όμως έχει 90 ήττες λιγότερες από τον Β. Αν με
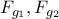 , παραστήσουμε τους "Fibonacci βαθμούς νίκης" των Α,Β αντίστοιχα, και αντικαταστήσουμε τις αντίστοιχες τιμές του καθενός στον τύπο
, παραστήσουμε τους "Fibonacci βαθμούς νίκης" των Α,Β αντίστοιχα, και αντικαταστήσουμε τις αντίστοιχες τιμές του καθενός στον τύπο 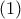 , τότε παίρνουμε
, τότε παίρνουμε  "Fibonacci βαθμούς νίκης" και
"Fibonacci βαθμούς νίκης" και  "Fibonacci βαθμούς νίκης". Από τη σύγκριση των αποτελεσμάτων αυτών, βγαίνει το συμπέρασμα, πως ο "ρίπτης" Α είναι καλύτερος από τον "ρίπτη" Β. Να, λοιπόν, μια ακόμη προσφορά των Μαθηματικών στον αθλητισμό.
"Fibonacci βαθμούς νίκης". Από τη σύγκριση των αποτελεσμάτων αυτών, βγαίνει το συμπέρασμα, πως ο "ρίπτης" Α είναι καλύτερος από τον "ρίπτη" Β. Να, λοιπόν, μια ακόμη προσφορά των Μαθηματικών στον αθλητισμό. Ασκηση: Ο Sandy Coufax είχε 165 νίκες και 87 ήττες και ο Jim Bunnig 224 νίκες και 184 ήττες. Ποιος είναι καλύτερος;
Σχέση ανάμεσα στο baseball, την ακολουθία Fibonacci και τη Χρυσή Αναλογία
Στο κρίσιμο σημείο, όπου οι νίκες συμπίπτουν με τους "Fibonacci βαθμούς νίκης", έχουμε τελικά από την
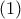 :
:
Να, λοιπόν, η Χρυσή Αναλογία
 και η σχέση της με το baseball.
και η σχέση της με το baseball.Βιβλιογραφία
Το υλικό, για να γραφτεί αυτή η εργασία, το δανειστήκαμε από: 1) Μπάμπη Τουμάση «Χρυσή Τομή – Fibonacci – Λαγοί και Λουλούδια», 2) QUANTUM, 3) Ιστορία του Ελληνικού Έθνους, 4) Πάπυρος-Larousse-Britannica»
Υ.Γ. 1 Στο επόμενο σημείωμα θα δούμε αν, για να παίξουμε καλό μπιλιάρδο, χρειάζεται να ξέρουμε Μαθηματικά
Υ.Γ. 2 Με το 30ο σημείωμα θα κλείσουμε το θέμα «ΓΙΑ ΠΟΙΟ ΛΟΓΟ ΔΙΔΑΣΚΟΥΜΕ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΑ ΠΑΙΔΙΑ;»
με εκτίμηση
Γιάννης Κερασαρίδης
- Συνημμένα
-
- Έγγραφο3.doc
- (499 KiB) Μεταφορτώθηκε 30 φορές
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
ΣΗΜΕΙΩΜΑ 29ο
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΜΠΙΛΙΑΡΔΟ
ή
πως θα γίνετε... η πιο "δυνατή στέκα"
Προλεγόμενα Όσο παράξενο κι αν σας φανεί, μαθηματικοί ερευνητές, μελετούν την τροχιά της μπάλας του μπιλιάρδου σε σενάρια τραπεζιών που έχουν τα πιο "τρελλά" καμπυλόγραμμα σχήματα. Να τι έγραφε ο Anatoly Savin: «Λύσεις σε προβλήματα του συγκεκριμένου τύπου μας βοηθούν να κατανοήσουμε τους νόμους της κίνησης των μορίων των αερίων ή δεσμών σωματιδίων σε κλειστούς όγκους, και τούτοι οι νόμοι είναι χρήσιμοι σε πολλές περιοχές της φυσικής, ιδιαίτερα στην κβαντική ηλεκτρονική. Τα μόρια ανακλώνται στα τοιχώματα ακριβώς όπως μια μπάλα του μπιλιάρδου στο τοίχωμα του τραπεζιού». Δεν πρέπει να ξεχνάμε ότι στα 1835 ο πε-ρίφημος Γάλλος Φυσικός – Μηχανικός - Μαθηματικός Gaspard Coriolis έγραψε ολόκληρο βιβλίο με θέμα «Η μαθηματική θεωρία των φαινομένων του μπιλιάρδου», στο οποίο μελετούσε τα μη κεντρικά χτυπήματα της μπάλας. Ένα μη κεντρικό χτύπημα της μπάλας την εξαναγκάζει, μεταξύ των άλλων, και σε περιστροφική κίνηση που, εξ αιτίας της τριβής της με την τσόχα του τραπε-ζιού, καμπυλώνει την τροχιά της.
{Απαραίτητες υπενθυμίσεις για αναγνώστες μαθητές
Γωνία πρόσπτωσης και γωνία ανάκλασης: Η ευθεία (ε) είναι εφαπτόμενη της καμπύλης C στο σημείο Α. Από τη Φυσική (Οπτική) γνωρίζουμε ότι η γωνία πρόσπτωσης είναι ίση με τη γωνία ανάκλασης. Δηλ. γων.ΧΑΖ=γων.ΖΑΨ
Συμμετρία ως προς άξονα: Θεωρούμε την ευθεία (ε) και ένα σημείο Α έξω απ' αυτήν . Από το σημείο Α φέρ-νουμε μια ευθεία (ε΄) κάθετη στην (ε), που τέμνει την (ε) στο σημείο Ο. Πάνω στην (ε΄) παίρνουμε ένα τμήμα ΟΑ1=ΟΑ. Τα σημεία Α και Α1 λέμε ότι είναι συμμετρικά μεταξύ τους με άξονα συμμετρίας την ευθεία (ε). Το σημείο Ο λέγεται προ-βολή του σημείου Α πάνω στην ευθεία (ε)}
Και τώρα, η ώρα του μπιλιάρδου
Μπιλιάρδο σε τραπέζι σχήματος ορθογωνίου
Πρόβλημα α΄ Στο τραπέζι μια μπάλα βρίσκεται στο σημείο Μ. Αν η κορυφή Δ του τραπεζιού είναι "τσέπη", ζητείται να βρεθεί η πορεία της μπάλας, για να μπει στην "τσέπη", αφού αυτή ανακλαστεί, υποχρεωτικά, στο τοίχωμα ΑΒ. (Σημ. "τσέπη" λέγεται η οπή που υπάρχει σε μια από τις κορυφές του τραπεζιού του μπιλιάρδου, στην οποία, ο παίκτης, πρέπει να κατευθύνει τις μπάλες)
Απάντηση
Έστω είναι η πορεία της μπάλας. Έστω ακόμη ότι το
είναι η πορεία της μπάλας. Έστω ακόμη ότι το  είναι το συμμετρικό του Δ με άξονα συμμετρίας το τοίχωμα ΑΒ του τραπεζιού. Σ’ αυτή την περίπτωση τα σημεία Μ, Κ,
είναι το συμμετρικό του Δ με άξονα συμμετρίας το τοίχωμα ΑΒ του τραπεζιού. Σ’ αυτή την περίπτωση τα σημεία Μ, Κ,  βρίσκονται στην ίδια ευθεία. Αρκεί λοιπόν ο παίκτης να βάλει την στέκα στην προέκταση του ευθγραμμου τμήματος
βρίσκονται στην ίδια ευθεία. Αρκεί λοιπόν ο παίκτης να βάλει την στέκα στην προέκταση του ευθγραμμου τμήματος  Μ (προς το μέρος του Μ) και να χτυπήσει κεντρικά τη μπάλα. Βέβαια εδώ μπαίνει ένα ερώτημα˙ πως θα εντοπίζουμε κάθε φορά τη θέση του
Μ (προς το μέρος του Μ) και να χτυπήσει κεντρικά τη μπάλα. Βέβαια εδώ μπαίνει ένα ερώτημα˙ πως θα εντοπίζουμε κάθε φορά τη θέση του  ; Υπάρχουν δύο απαντήσεις:
; Υπάρχουν δύο απαντήσεις:
Η πρώτη είναι να εξασκηθεί το μάτι ως προς τη θέση του σημείου Δ1 σε σχέση με αντικεί-μενα του περιβάλλοντος χώρου (εδώ πρέπει να σημειώσουμε ότι για οποιαδήποτε θέση της μπάλας Μ το σημείο Δ1 είναι πάντα στην ίδια θέση).
Η δεύτερη απάντηση είναι να τοποθετηθεί ένα μικρό καθρεφτάκι με την ανα-κλώσα επιφάνεια προς το μέρος του παίκτη, κάθετα προς την επιφάνεια του τραπεζιού και κατά μήκος του τοιχώματος ΑΒ. Αρκεί να χτυπήσουμε κεντρικά τη μπάλα, τοποθετώντας τη στέκα στην προέκταση της ευθείας που συνδέει τη μπάλα Μ με το είδωλο , της κορυφής Δ, ως προς τον καθρέφτη.
, της κορυφής Δ, ως προς τον καθρέφτη.
Πρόβλημα β΄ Στην τσόχα του μπιλιάρδου ΑΒΓΔ υπάρχουν δύο μπάλες, μια κόκκινη Κ και μια μαύρη Μ. Ζητείται, η μαύρη μπάλα να χτυπήσει την κόκκινη, αφού προηγούμενα ανα-κλαστεί πρώτα στο τοίχωμα ΓΒ και μετά στο τοίχωμα ΒΑ.
Απάντηση
Θεωρούμε το παραλ/μο που είναι συμμετρικό του ΑΒΓΔ (με άξονα το ΒΓ). Θεωρούμε, ακόμη, το παραλ/μο
που είναι συμμετρικό του ΑΒΓΔ (με άξονα το ΒΓ). Θεωρούμε, ακόμη, το παραλ/μο  που είναι συμμετρικό του
που είναι συμμετρικό του  (με άξονα το
(με άξονα το  ). Έστω
). Έστω  το συμμετρικό της Κ ( με άξονα το ΒΓ) και
το συμμετρικό της Κ ( με άξονα το ΒΓ) και  το συμμετρικό του
το συμμετρικό του  (με άξονα το
(με άξονα το  )
)
Η ευθεία που συνδέει τα σημεία Μ, τέμνει το "τοίχωμα" ΒΓ στο σημείο Π και το "τοίχωμα"
τέμνει το "τοίχωμα" ΒΓ στο σημείο Π και το "τοίχωμα"  στο σημείο
στο σημείο  . Αν Λ είναι το συμμετρικό του
. Αν Λ είναι το συμμετρικό του  (με άξονα συμμετρίας το τοίχωμα ΒΓ), τότε η σωστή πορεία της μπάλας είναι η
(με άξονα συμμετρίας το τοίχωμα ΒΓ), τότε η σωστή πορεία της μπάλας είναι η 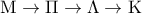 . Άρα ο παίκτης, αρκεί να χτυπήσει κεντρικά την μπάλα Μ, τοποθετώντας την στέκα στην προέκταση του ευθύγραμμου τμήματος
. Άρα ο παίκτης, αρκεί να χτυπήσει κεντρικά την μπάλα Μ, τοποθετώντας την στέκα στην προέκταση του ευθύγραμμου τμήματος 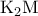 Μ. Οι τρόποι με τους οποίους πετυχαίνουμε κάτι τέτοιο είναι οι ίδιοι, (όπως στην περίπτωση του προ-βλήματος α΄), μόνο που τώρα χρησιμοποιούμε δύο καθρεφτάκια˙ ένα κατά μήκος του τοιχώμα-τος ΒΓ και ένα κατά μήκος του τοιχώματος ΒΑ.
Μ. Οι τρόποι με τους οποίους πετυχαίνουμε κάτι τέτοιο είναι οι ίδιοι, (όπως στην περίπτωση του προ-βλήματος α΄), μόνο που τώρα χρησιμοποιούμε δύο καθρεφτάκια˙ ένα κατά μήκος του τοιχώμα-τος ΒΓ και ένα κατά μήκος του τοιχώματος ΒΑ.
Το μπιλιάρδο και το πρόβλημα του S. Pankov
Ένας γυάλινος αγωγός φωτός έχει τη μορφή κόλουρου κώνου και είναι καλυμμένος στο εσωτερικό του από άργυρο (καθρέφτης). Τα επίπεδα των βάσεων του κώνου είναι κάθετα στον άξονά του, οι διάμετροί τους είναι d, και το ύψος
και το ύψος  . Μια δέσμη φωτός, παράλληλη με τον άξονα του κώνου, προσπίπτει στη μεγάλη του βάση (η φωτεινή δέσμη δεν είναι απαραίτητο να περιέχει τον άξονα του κώνου).
. Μια δέσμη φωτός, παράλληλη με τον άξονα του κώνου, προσπίπτει στη μεγάλη του βάση (η φωτεινή δέσμη δεν είναι απαραίτητο να περιέχει τον άξονα του κώνου).
Ερώτημα: Όλες οι ακτίνες της φωτεινής δέσμης θα βγουν από τη μικρή βάση αφού υποστούν πολλαπλές ανακλάσεις στα εσωτερικά τοιχώματα;
Υπόδειξη: το ότι η επιφάνεια είναι κωνική δεν έχει καμιά σημασία. Αρκεί να εξετάσετε τις "ακραίες" φωτεινές ακτίνες που προσπίπτουν στο σύνορο της μεγάλης βάσης.
Υ.Γ. Με το επόμενο [ΣΗΜΕΙΩΜΑ 30ο], κλείνει η σειρά των σημειωμάτων μας με θέμα "Για ποιο λόγο διδάσκουμε τα Μαθηματικά στα παιδιά". Αυτό, όμως, δεν σημαίνει πως εξαντλήθηκε το θέμα, γιατί ακριβώς μπορούμε να το δούμε από πολλές οπτικές [πχ., η αισθητική απόλαυση που μπορεί να μας προσφέρει η ενασχόληση με τα Μαθηματικά κλπ, κλπ]
με εκτίμηση
Γιάννης Κερασαρίδης
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΜΠΙΛΙΑΡΔΟ
ή
πως θα γίνετε... η πιο "δυνατή στέκα"
Προλεγόμενα Όσο παράξενο κι αν σας φανεί, μαθηματικοί ερευνητές, μελετούν την τροχιά της μπάλας του μπιλιάρδου σε σενάρια τραπεζιών που έχουν τα πιο "τρελλά" καμπυλόγραμμα σχήματα. Να τι έγραφε ο Anatoly Savin: «Λύσεις σε προβλήματα του συγκεκριμένου τύπου μας βοηθούν να κατανοήσουμε τους νόμους της κίνησης των μορίων των αερίων ή δεσμών σωματιδίων σε κλειστούς όγκους, και τούτοι οι νόμοι είναι χρήσιμοι σε πολλές περιοχές της φυσικής, ιδιαίτερα στην κβαντική ηλεκτρονική. Τα μόρια ανακλώνται στα τοιχώματα ακριβώς όπως μια μπάλα του μπιλιάρδου στο τοίχωμα του τραπεζιού». Δεν πρέπει να ξεχνάμε ότι στα 1835 ο πε-ρίφημος Γάλλος Φυσικός – Μηχανικός - Μαθηματικός Gaspard Coriolis έγραψε ολόκληρο βιβλίο με θέμα «Η μαθηματική θεωρία των φαινομένων του μπιλιάρδου», στο οποίο μελετούσε τα μη κεντρικά χτυπήματα της μπάλας. Ένα μη κεντρικό χτύπημα της μπάλας την εξαναγκάζει, μεταξύ των άλλων, και σε περιστροφική κίνηση που, εξ αιτίας της τριβής της με την τσόχα του τραπε-ζιού, καμπυλώνει την τροχιά της.
{Απαραίτητες υπενθυμίσεις για αναγνώστες μαθητές
Γωνία πρόσπτωσης και γωνία ανάκλασης: Η ευθεία (ε) είναι εφαπτόμενη της καμπύλης C στο σημείο Α. Από τη Φυσική (Οπτική) γνωρίζουμε ότι η γωνία πρόσπτωσης είναι ίση με τη γωνία ανάκλασης. Δηλ. γων.ΧΑΖ=γων.ΖΑΨ
Συμμετρία ως προς άξονα: Θεωρούμε την ευθεία (ε) και ένα σημείο Α έξω απ' αυτήν . Από το σημείο Α φέρ-νουμε μια ευθεία (ε΄) κάθετη στην (ε), που τέμνει την (ε) στο σημείο Ο. Πάνω στην (ε΄) παίρνουμε ένα τμήμα ΟΑ1=ΟΑ. Τα σημεία Α και Α1 λέμε ότι είναι συμμετρικά μεταξύ τους με άξονα συμμετρίας την ευθεία (ε). Το σημείο Ο λέγεται προ-βολή του σημείου Α πάνω στην ευθεία (ε)}
Και τώρα, η ώρα του μπιλιάρδου
Μπιλιάρδο σε τραπέζι σχήματος ορθογωνίου
Πρόβλημα α΄ Στο τραπέζι μια μπάλα βρίσκεται στο σημείο Μ. Αν η κορυφή Δ του τραπεζιού είναι "τσέπη", ζητείται να βρεθεί η πορεία της μπάλας, για να μπει στην "τσέπη", αφού αυτή ανακλαστεί, υποχρεωτικά, στο τοίχωμα ΑΒ. (Σημ. "τσέπη" λέγεται η οπή που υπάρχει σε μια από τις κορυφές του τραπεζιού του μπιλιάρδου, στην οποία, ο παίκτης, πρέπει να κατευθύνει τις μπάλες)
Απάντηση
Έστω
 είναι η πορεία της μπάλας. Έστω ακόμη ότι το
είναι η πορεία της μπάλας. Έστω ακόμη ότι το  είναι το συμμετρικό του Δ με άξονα συμμετρίας το τοίχωμα ΑΒ του τραπεζιού. Σ’ αυτή την περίπτωση τα σημεία Μ, Κ,
είναι το συμμετρικό του Δ με άξονα συμμετρίας το τοίχωμα ΑΒ του τραπεζιού. Σ’ αυτή την περίπτωση τα σημεία Μ, Κ,  βρίσκονται στην ίδια ευθεία. Αρκεί λοιπόν ο παίκτης να βάλει την στέκα στην προέκταση του ευθγραμμου τμήματος
βρίσκονται στην ίδια ευθεία. Αρκεί λοιπόν ο παίκτης να βάλει την στέκα στην προέκταση του ευθγραμμου τμήματος  Μ (προς το μέρος του Μ) και να χτυπήσει κεντρικά τη μπάλα. Βέβαια εδώ μπαίνει ένα ερώτημα˙ πως θα εντοπίζουμε κάθε φορά τη θέση του
Μ (προς το μέρος του Μ) και να χτυπήσει κεντρικά τη μπάλα. Βέβαια εδώ μπαίνει ένα ερώτημα˙ πως θα εντοπίζουμε κάθε φορά τη θέση του  ; Υπάρχουν δύο απαντήσεις:
; Υπάρχουν δύο απαντήσεις: Η πρώτη είναι να εξασκηθεί το μάτι ως προς τη θέση του σημείου Δ1 σε σχέση με αντικεί-μενα του περιβάλλοντος χώρου (εδώ πρέπει να σημειώσουμε ότι για οποιαδήποτε θέση της μπάλας Μ το σημείο Δ1 είναι πάντα στην ίδια θέση).
Η δεύτερη απάντηση είναι να τοποθετηθεί ένα μικρό καθρεφτάκι με την ανα-κλώσα επιφάνεια προς το μέρος του παίκτη, κάθετα προς την επιφάνεια του τραπεζιού και κατά μήκος του τοιχώματος ΑΒ. Αρκεί να χτυπήσουμε κεντρικά τη μπάλα, τοποθετώντας τη στέκα στην προέκταση της ευθείας που συνδέει τη μπάλα Μ με το είδωλο
 , της κορυφής Δ, ως προς τον καθρέφτη.
, της κορυφής Δ, ως προς τον καθρέφτη. Πρόβλημα β΄ Στην τσόχα του μπιλιάρδου ΑΒΓΔ υπάρχουν δύο μπάλες, μια κόκκινη Κ και μια μαύρη Μ. Ζητείται, η μαύρη μπάλα να χτυπήσει την κόκκινη, αφού προηγούμενα ανα-κλαστεί πρώτα στο τοίχωμα ΓΒ και μετά στο τοίχωμα ΒΑ.
Απάντηση
Θεωρούμε το παραλ/μο
 που είναι συμμετρικό του ΑΒΓΔ (με άξονα το ΒΓ). Θεωρούμε, ακόμη, το παραλ/μο
που είναι συμμετρικό του ΑΒΓΔ (με άξονα το ΒΓ). Θεωρούμε, ακόμη, το παραλ/μο  που είναι συμμετρικό του
που είναι συμμετρικό του  (με άξονα το
(με άξονα το  ). Έστω
). Έστω  το συμμετρικό της Κ ( με άξονα το ΒΓ) και
το συμμετρικό της Κ ( με άξονα το ΒΓ) και  το συμμετρικό του
το συμμετρικό του  (με άξονα το
(με άξονα το  )
)Η ευθεία που συνδέει τα σημεία Μ,
 τέμνει το "τοίχωμα" ΒΓ στο σημείο Π και το "τοίχωμα"
τέμνει το "τοίχωμα" ΒΓ στο σημείο Π και το "τοίχωμα"  στο σημείο
στο σημείο  . Αν Λ είναι το συμμετρικό του
. Αν Λ είναι το συμμετρικό του  (με άξονα συμμετρίας το τοίχωμα ΒΓ), τότε η σωστή πορεία της μπάλας είναι η
(με άξονα συμμετρίας το τοίχωμα ΒΓ), τότε η σωστή πορεία της μπάλας είναι η 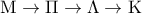 . Άρα ο παίκτης, αρκεί να χτυπήσει κεντρικά την μπάλα Μ, τοποθετώντας την στέκα στην προέκταση του ευθύγραμμου τμήματος
. Άρα ο παίκτης, αρκεί να χτυπήσει κεντρικά την μπάλα Μ, τοποθετώντας την στέκα στην προέκταση του ευθύγραμμου τμήματος 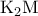 Μ. Οι τρόποι με τους οποίους πετυχαίνουμε κάτι τέτοιο είναι οι ίδιοι, (όπως στην περίπτωση του προ-βλήματος α΄), μόνο που τώρα χρησιμοποιούμε δύο καθρεφτάκια˙ ένα κατά μήκος του τοιχώμα-τος ΒΓ και ένα κατά μήκος του τοιχώματος ΒΑ.
Μ. Οι τρόποι με τους οποίους πετυχαίνουμε κάτι τέτοιο είναι οι ίδιοι, (όπως στην περίπτωση του προ-βλήματος α΄), μόνο που τώρα χρησιμοποιούμε δύο καθρεφτάκια˙ ένα κατά μήκος του τοιχώμα-τος ΒΓ και ένα κατά μήκος του τοιχώματος ΒΑ. Το μπιλιάρδο και το πρόβλημα του S. Pankov
Ένας γυάλινος αγωγός φωτός έχει τη μορφή κόλουρου κώνου και είναι καλυμμένος στο εσωτερικό του από άργυρο (καθρέφτης). Τα επίπεδα των βάσεων του κώνου είναι κάθετα στον άξονά του, οι διάμετροί τους είναι d,
 και το ύψος
και το ύψος  . Μια δέσμη φωτός, παράλληλη με τον άξονα του κώνου, προσπίπτει στη μεγάλη του βάση (η φωτεινή δέσμη δεν είναι απαραίτητο να περιέχει τον άξονα του κώνου).
. Μια δέσμη φωτός, παράλληλη με τον άξονα του κώνου, προσπίπτει στη μεγάλη του βάση (η φωτεινή δέσμη δεν είναι απαραίτητο να περιέχει τον άξονα του κώνου). Ερώτημα: Όλες οι ακτίνες της φωτεινής δέσμης θα βγουν από τη μικρή βάση αφού υποστούν πολλαπλές ανακλάσεις στα εσωτερικά τοιχώματα;
Υπόδειξη: το ότι η επιφάνεια είναι κωνική δεν έχει καμιά σημασία. Αρκεί να εξετάσετε τις "ακραίες" φωτεινές ακτίνες που προσπίπτουν στο σύνορο της μεγάλης βάσης.
Υ.Γ. Με το επόμενο [ΣΗΜΕΙΩΜΑ 30ο], κλείνει η σειρά των σημειωμάτων μας με θέμα "Για ποιο λόγο διδάσκουμε τα Μαθηματικά στα παιδιά". Αυτό, όμως, δεν σημαίνει πως εξαντλήθηκε το θέμα, γιατί ακριβώς μπορούμε να το δούμε από πολλές οπτικές [πχ., η αισθητική απόλαυση που μπορεί να μας προσφέρει η ενασχόληση με τα Μαθηματικά κλπ, κλπ]
με εκτίμηση
Γιάννης Κερασαρίδης
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
ΣΗΜΕΙΩΜΑ 30ο [ΤΕΛΕΥΤΑΙΟ]
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΑΙΣΘΗΤΙΚΗ
Προλεγόμενα Με το σημείωμα τούτο κλείνουμε αυτόν τον φάκελο [«Για ποιο λόγο διδάσκουμε τα Μαθηματικά στα παιδιά»], όχι γιατί έχει εξαντληθεί το θέμα, αλλά γιατί υπάρχει α) μια ολόκληρη θάλασσα σχετικών θεμάτων και β) γιατί ο φιλόξενος χώρος του ιστοτόπου μας είναι πολύτιμος για τους συναδέλφους. Κλείνοντας, θεωρήσαμε πως θα ήταν μέγιστη παράλειψή μας, αν δεν παραθέταμε την άποψη του Ακαδημαϊκού Φίλωνος Βασιλείου, για τη σχέση της επιστήμης των Μαθηματικών και της αισθητικής.
το κείμενο
«Είναι δύσκολο για τους πολλούς να κατανοήσουν την ύπαρξη οποιασδήποτε συγγένειας ανάμεσα στα Μαθηματικά και την Αισθητική. Κι αυτό, γιατί ο κοινός άνθρωπος θεωρεί τα Μαθηματικά ως μια επιστήμη σκοτεινή και ψυχρή, που περισσότερο αποκρούει παρά θέλγει και που γι αυτό κάθε αισθητικό στοιχείο της είναι ξένο και απρόσιτο. Ο ίδιος ακόμα συναρτά την ύπαρξη του Ωραίου μόνο με τη Φύση και την Καλλιτεχνία. Δεν μπορεί λοιπόν να σκεφτεί με ποιό τρόπο μια τόσο έκδηλα νοητική δραστηριότητα, όπως εκείνη του μαθηματικού, είναι δυνατόν να σχετίζεται με τον συναισθηματικό κόσμο, μέσα στον οποίον πολλές φορές ο καλλιτέχνης κινείται και δημιουργεί.
Ωστόσο, αν δεν σταθεί κανείς στην απλοϊκή αυτή αντίληψη και αν ζητήσει ακόμα κι ως μη ειδικός να ερευνήσει για βαθύτερες αναλογίες, δεν θ' αργήσει να εντυπωσιαστεί από πολύ στενές ομοιότητες, που υπάρχουν στις επιφανειακά τόσο διαφορετικές λειτουργίες του μαθηματικού και του καλλιτεχνικού νου. Δεν αποκλείεται η έκπληξη να οδηγήσει ακόμα και στην ακραία άποψη, πως δηλαδή τα Μαθηματικά πρέπει κι αυτά να θεωρηθούν ως μια Καλή Τέχνη.
Οι ομοιότητες, για τις οποίες έγινε λόγος, αφορούν είτε στον τρόπο λειτουργίας του δημιουργικού νου, στις δύο εξεταζόμενες περιπτώσεις , είτε σε κοινές βασικές έννοιες που χρησιμοποιεί τόσον ο μαθηματικός όσον και ο καλλιτέχνης. Εξάλλου η θεώρηση καθ' εαυτήν οποιασδήποτε μαθηματικής δομής μαζί με την χρησιμοποιούμενη μέθοδο δόμησής της παρέχει πραγματικά μια καθαρά αισθητική απόλαυση με τη θαυμαστή αρμονία αρχιτεκτονικής και την κομψότητα στην έκθεση των θεωριών της»
............................................................................................................................................
«Μια βασική τώρα έννοια, κοινή στα Μαθηματικά και στην Καλλιτεχνία, εκτός από τις γνωστές σε όλους χ ρ υ σ ή τ ο μ ή και σ υ μ μ ε τα ρ ί α, είναι εκείνη του σ υ μ π λ έ γ μ α τ ο ς , αλλιώς ο μ ά δ α ς , που πηγάζει απ' αυτήν την έννοια της συμμετρίας. Σε ένα γεωμετρικό σχήμα συμμετρία είναι μια αμφιμονοσήμαντη απεικόνιση των σημείων του σχήματος επάνω στα ίδια αυτά σημεία με διατήρηση της απόστασής τους ανά δυο. Η πράξη της αλλεπάλληλης εφαρμογής δύο τέτοιων απεικονίσεων, που έχει ορισμένες ιδιότητες, παρέχει ένα σύστημα από απεικονίσεις. Γενίκευση του συστήματος αυτού σε οποιαδήποτε αφηρημένα στοιχεία (στη θέση απεικονίσεων) για τα οποία ορίζεται, μια μονοσήμαντη διμελής πράξη που υπακούει. σε ίδιες ιδιότητες όπως οι απεικονίσεις, αποτελεί αυτό που ονομάζουμε σύστημα συμπλεγμάτων.
Η έννοια του συμπλέγματος εισέρχεται σε κάθε σχεδόν κλάδο των σύγχρονων Μαθηματικών. Ιδιαίτερα μια από τις πιο βαθιές και ωραίες μαθηματικές θεωρίες, η λεγόμενη θεωρία του Ε. Galois , έχει τις ρίζες της στα συμπλέγματα. Στις Καλές Τέχνες, ιδιαίτερα στη Μουσική, η έννοια του συμπλέγματος παίζει επίσης σπουδαιότατο ρόλο. Έτσι, η "Τέχνη της Φούγκας" του J.S. Bach δείχνει, πόσο βαθειά εισδύουν στη μουσική σύνθεση μαθηματικές έννοιες. Άλλωστε η σημασία της επίδρασης καταφαίνεται και από το γεγονός, ότι το έργο αυτό θεωρείται ως το πιο μεγαλεπήβολο δείγμα σύνθεσης στη Μουσική της Δύσης. Δεν μπορεί φυσικά να υποστηριχθεί, ότι ο συνθέτης του υπ' όψη έργου καθοδηγείτο ενσυνείδητα από κάποια μαθηματική θεωρία. Ακριβώς όμως η σύνθεση αυτή καταδεικνύει, μια στενή συγγένεια ανάμεσα στη Μουσική και στα Μαθηματικά.
Από μουσικοκριτικές αναλύσεις της Σονάτας 15, Op.28 για πιάνο του L.van Beethoven συμπεραίνομαι ακόμα, ότι, το έργο αυτό έχει συντεθεί, φυσικά με τρόπο μη συνειδητό, απάνω σε μαθηματικά πρότυπα, συγκεκριμένα στη θεωρία των συμπλεγμάτων. Το ίδιο μπορεί να ειπωθεί και, για άλλες μουσικές
συνθέσεις, όπως για μερικά όχι τόσο γνωστά έργα του W.Α. Μozart και του J. Haydn .
Αλλά και σχετικά με την ίδια τη δομή μιας μαθηματικής θεωρίας υπάρχει υψηλή αισθητική απόλαυση, που για να τη δοκιμάσει όμως κανείς απαιτείται - όπως και στην Τέχνη - προηγούμενη καλλιέργεια αυτού που ονομάζομε μ α θ η μ α τ ι κ ό γ ο ύ σ τ ο, ανάλογο με το καλλιτεχνικό. Την αισθητική απόλαυση, στην περίπτωση μιας μαθηματικής θεωρίας, τη δίνει η τ ε λ ε ι ό τ η τ α στις αποδείξεις, η α ρ μ ο ν ί α ανάμεσα στα διάφορα μέρη και η αυστηρή α ρ χ ι τ ε κ τ ο ν ι κ ή του όλου. Στην αρμονία αυτή, τη συμμετρία και την πλήρη ισορρόπηση των μερών, αποδίδει ο Poincare την αίσθηση της κομψότητας, που χαρακτηρίζει τα Μαθηματικά.
Αναφορικά με τη μέθοδο δόμησης σημειώνουμε, ότι ένα από τα κύρια εφόδια στα Μαθηματικά είναι οι συμβολικοί τ ύ π ο ι, που αντιπροσωπεύουν αυτές τις ίδιες τις μαθηματικές ι δ έ ε ς. Ώστε, η ακολουθούμενη αξιωματική μεθοδολογία για τον χειρισμό των τύπων αυτών εμφανίζει έναν πρόσθετο τομέα, άξιο να εξεταστεί για τον αισθητικό του χαρακτήρα.
Μια από τις σύγχρονες Σχολές, που θέλει να ερμηνεύσει την ίδρυση των Μαθηματικών, είναι η "Φορμαλιστική Σχολή" που οφείλεται στον D. Hilbert . Πρόκειται για την θεώρηση εκείνη των Μαθηματικών, που τα βλέπει κανείς πρώτα ως ένα σύστημα από τύπους, χωρίς οποιαδήποτε σημασία, και από πράξεις επάνω στους τύπους αυτούς - πράξεις που εκτελούνται σύμφωνα με ορισμένους κανόνες. Στο σύστημα αυτό ξεκινά κανείς από ορισμένους τύπους-αξιώματα και απ' αυτά συνάγει, τους λοιπούς τύπους του συστήματος με βάση τις δοθείσες τυπικές πράξεις. Έπειτα η εφαρμογή μιας άλλης , εποπτικής τη φορά αυτή, θεωρίας - που φέρει το όνομα Μεταμαθηματικά-συμπληρώνει αυτό που ονομάζουμε, κατά τον D. Hilbert, Μαθηματικά. Είναι πολύ προσφυής ο παραλληλισμός της φορμαλιστικής θεωρίας με το γνωστό παιγνίδι του σκακιού. Ο παραλληλισμός αυτός πραγματοποιείται, αν αντιστοιχήσαμε τους τύπους-αξιώματα με την αρχική θέση που έχουν οι φιγούρες στο παιγνίδι, τον τρόπο παραγωγής των τύπων με τους κανόνες κινήσεων στις φιγούρες και τις αποδείξεις με τις σειρές κινήσεων του παιγνιδιού.
Όσα είπαμε πιο πάνω για τον φορμαλιστικό τρόπο δόμησης των Μαθηματικών νομίζομε ότι αποκαλύπτουν με ενάργεια τον αισθητικό χαρακτήρα της μεθόδου αυτής , μεθόδου που σε αδρές γραμμές μας δίνει μια πλήρη εποπτική εικόνα της λειτουργίας σε ένα τόσο εκτεταμένο και πολυδαίδαλο οικοδόμημα»
.........................................................................................................................................
«Εκείνο που θα μπορούσε να ερωτήσει κανείς είναι, αν υπάρχουν αντικειμενικά κριτήρια για την αξιολόγηση και την συγκριτική αποτίμηση των αισθητικών αξιών μέσα σε μια και την ίδια μαθηματική δημιουργία ή στις αισθητικές αξίες διαφόρων δημιουργιών. Η απάντηση στο ερώτημα αυτό δεν είναι καθόλου εύκολη, για να μη πούμε πως στην ουσία είναι, αρνητική. Είναι, φανερό ότι, η ύπαρξη αντικειμενικού κριτηρίου αποτίμησης των μαθηματικών αξιών ισοδυναμεί με την εύρεση κανόνων για τη δημιουργία αισθητικών αριστουργημάτων. Ούτε ακόμα είναι, δυνατή η συγχώνευση σε ένα κανόνα των διαφόρων γνωρισμάτων για καθένα χωριστά μαθηματικό επίτευγμα, που έχει, αισθητική αξία. Το βέβαιο είναι,, ότι, κ ά θ ε μαθηματικό επίτευγμα έχει, τη δική του αισθητική αξία και ότι, κατά κάποιο τρόπο, θα μπορούσε κανείς να το αντιμετωπίσει ως ένα έργο τέχνης. Στο σημείο αυτό ας μη ξεχνούμε, ότι, ο Η. Weyl παρομοιάζει την μαθηματική με την μουσική δημιουργία. Υπάρχουν αν και σπανιότερα, μαθηματικοί που αισθάνονται, την ανάγκη να προσφύγουν στον καλλιτέχνη για την αισθητική αξιολόγηση του έργου τους. Δεν θα ήταν άραγε επιθυμητό να βρίσκονταν κάποτε και καλλιτέχνες που θα συμβουλεύονταν τους μαθηματικούς για τον ίδιο λόγο;
Ένα τελευταίο ερώτημα άφορα στο κατά πόσον η συγκίνηση, η ευαισθησία και γενικά ο συναισθηματικός κόσμος του μαθηματικού, ασκεί οποιαδήποτε επίδραση στο δημιουργικό του έργο, ανάλογα με ότι, συμβαίνει, στον καλλιτέχνη. Θέλουμε να πιστεύουμε, ότι, και στο σημείο αυτό υπάρχει, αναλογία ανάμεσα στο έργο ενός καλλιτέχνη και ενός μαθηματικού, αφού άλλωστε η αγάπη και το πάθος για την επιστήμη του οδηγούν τον μαθηματικό στο δημιουργικό του έργο»
Φίλων ΒΑΣΙΛΕΙΟΥ, της Ακαδημίας Αθηνών
[πηγή: Μ.Ε., τεύχ.9 (Νέα Σειρά), εκδ. ΕΜΕ, 1978]
με εκτίμηση
Γιάννης Κερασαρίδης
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΑΙΣΘΗΤΙΚΗ
Προλεγόμενα Με το σημείωμα τούτο κλείνουμε αυτόν τον φάκελο [«Για ποιο λόγο διδάσκουμε τα Μαθηματικά στα παιδιά»], όχι γιατί έχει εξαντληθεί το θέμα, αλλά γιατί υπάρχει α) μια ολόκληρη θάλασσα σχετικών θεμάτων και β) γιατί ο φιλόξενος χώρος του ιστοτόπου μας είναι πολύτιμος για τους συναδέλφους. Κλείνοντας, θεωρήσαμε πως θα ήταν μέγιστη παράλειψή μας, αν δεν παραθέταμε την άποψη του Ακαδημαϊκού Φίλωνος Βασιλείου, για τη σχέση της επιστήμης των Μαθηματικών και της αισθητικής.
το κείμενο
«Είναι δύσκολο για τους πολλούς να κατανοήσουν την ύπαρξη οποιασδήποτε συγγένειας ανάμεσα στα Μαθηματικά και την Αισθητική. Κι αυτό, γιατί ο κοινός άνθρωπος θεωρεί τα Μαθηματικά ως μια επιστήμη σκοτεινή και ψυχρή, που περισσότερο αποκρούει παρά θέλγει και που γι αυτό κάθε αισθητικό στοιχείο της είναι ξένο και απρόσιτο. Ο ίδιος ακόμα συναρτά την ύπαρξη του Ωραίου μόνο με τη Φύση και την Καλλιτεχνία. Δεν μπορεί λοιπόν να σκεφτεί με ποιό τρόπο μια τόσο έκδηλα νοητική δραστηριότητα, όπως εκείνη του μαθηματικού, είναι δυνατόν να σχετίζεται με τον συναισθηματικό κόσμο, μέσα στον οποίον πολλές φορές ο καλλιτέχνης κινείται και δημιουργεί.
Ωστόσο, αν δεν σταθεί κανείς στην απλοϊκή αυτή αντίληψη και αν ζητήσει ακόμα κι ως μη ειδικός να ερευνήσει για βαθύτερες αναλογίες, δεν θ' αργήσει να εντυπωσιαστεί από πολύ στενές ομοιότητες, που υπάρχουν στις επιφανειακά τόσο διαφορετικές λειτουργίες του μαθηματικού και του καλλιτεχνικού νου. Δεν αποκλείεται η έκπληξη να οδηγήσει ακόμα και στην ακραία άποψη, πως δηλαδή τα Μαθηματικά πρέπει κι αυτά να θεωρηθούν ως μια Καλή Τέχνη.
Οι ομοιότητες, για τις οποίες έγινε λόγος, αφορούν είτε στον τρόπο λειτουργίας του δημιουργικού νου, στις δύο εξεταζόμενες περιπτώσεις , είτε σε κοινές βασικές έννοιες που χρησιμοποιεί τόσον ο μαθηματικός όσον και ο καλλιτέχνης. Εξάλλου η θεώρηση καθ' εαυτήν οποιασδήποτε μαθηματικής δομής μαζί με την χρησιμοποιούμενη μέθοδο δόμησής της παρέχει πραγματικά μια καθαρά αισθητική απόλαυση με τη θαυμαστή αρμονία αρχιτεκτονικής και την κομψότητα στην έκθεση των θεωριών της»
............................................................................................................................................
«Μια βασική τώρα έννοια, κοινή στα Μαθηματικά και στην Καλλιτεχνία, εκτός από τις γνωστές σε όλους χ ρ υ σ ή τ ο μ ή και σ υ μ μ ε τα ρ ί α, είναι εκείνη του σ υ μ π λ έ γ μ α τ ο ς , αλλιώς ο μ ά δ α ς , που πηγάζει απ' αυτήν την έννοια της συμμετρίας. Σε ένα γεωμετρικό σχήμα συμμετρία είναι μια αμφιμονοσήμαντη απεικόνιση των σημείων του σχήματος επάνω στα ίδια αυτά σημεία με διατήρηση της απόστασής τους ανά δυο. Η πράξη της αλλεπάλληλης εφαρμογής δύο τέτοιων απεικονίσεων, που έχει ορισμένες ιδιότητες, παρέχει ένα σύστημα από απεικονίσεις. Γενίκευση του συστήματος αυτού σε οποιαδήποτε αφηρημένα στοιχεία (στη θέση απεικονίσεων) για τα οποία ορίζεται, μια μονοσήμαντη διμελής πράξη που υπακούει. σε ίδιες ιδιότητες όπως οι απεικονίσεις, αποτελεί αυτό που ονομάζουμε σύστημα συμπλεγμάτων.
Η έννοια του συμπλέγματος εισέρχεται σε κάθε σχεδόν κλάδο των σύγχρονων Μαθηματικών. Ιδιαίτερα μια από τις πιο βαθιές και ωραίες μαθηματικές θεωρίες, η λεγόμενη θεωρία του Ε. Galois , έχει τις ρίζες της στα συμπλέγματα. Στις Καλές Τέχνες, ιδιαίτερα στη Μουσική, η έννοια του συμπλέγματος παίζει επίσης σπουδαιότατο ρόλο. Έτσι, η "Τέχνη της Φούγκας" του J.S. Bach δείχνει, πόσο βαθειά εισδύουν στη μουσική σύνθεση μαθηματικές έννοιες. Άλλωστε η σημασία της επίδρασης καταφαίνεται και από το γεγονός, ότι το έργο αυτό θεωρείται ως το πιο μεγαλεπήβολο δείγμα σύνθεσης στη Μουσική της Δύσης. Δεν μπορεί φυσικά να υποστηριχθεί, ότι ο συνθέτης του υπ' όψη έργου καθοδηγείτο ενσυνείδητα από κάποια μαθηματική θεωρία. Ακριβώς όμως η σύνθεση αυτή καταδεικνύει, μια στενή συγγένεια ανάμεσα στη Μουσική και στα Μαθηματικά.
Από μουσικοκριτικές αναλύσεις της Σονάτας 15, Op.28 για πιάνο του L.van Beethoven συμπεραίνομαι ακόμα, ότι, το έργο αυτό έχει συντεθεί, φυσικά με τρόπο μη συνειδητό, απάνω σε μαθηματικά πρότυπα, συγκεκριμένα στη θεωρία των συμπλεγμάτων. Το ίδιο μπορεί να ειπωθεί και, για άλλες μουσικές
συνθέσεις, όπως για μερικά όχι τόσο γνωστά έργα του W.Α. Μozart και του J. Haydn .
Αλλά και σχετικά με την ίδια τη δομή μιας μαθηματικής θεωρίας υπάρχει υψηλή αισθητική απόλαυση, που για να τη δοκιμάσει όμως κανείς απαιτείται - όπως και στην Τέχνη - προηγούμενη καλλιέργεια αυτού που ονομάζομε μ α θ η μ α τ ι κ ό γ ο ύ σ τ ο, ανάλογο με το καλλιτεχνικό. Την αισθητική απόλαυση, στην περίπτωση μιας μαθηματικής θεωρίας, τη δίνει η τ ε λ ε ι ό τ η τ α στις αποδείξεις, η α ρ μ ο ν ί α ανάμεσα στα διάφορα μέρη και η αυστηρή α ρ χ ι τ ε κ τ ο ν ι κ ή του όλου. Στην αρμονία αυτή, τη συμμετρία και την πλήρη ισορρόπηση των μερών, αποδίδει ο Poincare την αίσθηση της κομψότητας, που χαρακτηρίζει τα Μαθηματικά.
Αναφορικά με τη μέθοδο δόμησης σημειώνουμε, ότι ένα από τα κύρια εφόδια στα Μαθηματικά είναι οι συμβολικοί τ ύ π ο ι, που αντιπροσωπεύουν αυτές τις ίδιες τις μαθηματικές ι δ έ ε ς. Ώστε, η ακολουθούμενη αξιωματική μεθοδολογία για τον χειρισμό των τύπων αυτών εμφανίζει έναν πρόσθετο τομέα, άξιο να εξεταστεί για τον αισθητικό του χαρακτήρα.
Μια από τις σύγχρονες Σχολές, που θέλει να ερμηνεύσει την ίδρυση των Μαθηματικών, είναι η "Φορμαλιστική Σχολή" που οφείλεται στον D. Hilbert . Πρόκειται για την θεώρηση εκείνη των Μαθηματικών, που τα βλέπει κανείς πρώτα ως ένα σύστημα από τύπους, χωρίς οποιαδήποτε σημασία, και από πράξεις επάνω στους τύπους αυτούς - πράξεις που εκτελούνται σύμφωνα με ορισμένους κανόνες. Στο σύστημα αυτό ξεκινά κανείς από ορισμένους τύπους-αξιώματα και απ' αυτά συνάγει, τους λοιπούς τύπους του συστήματος με βάση τις δοθείσες τυπικές πράξεις. Έπειτα η εφαρμογή μιας άλλης , εποπτικής τη φορά αυτή, θεωρίας - που φέρει το όνομα Μεταμαθηματικά-συμπληρώνει αυτό που ονομάζουμε, κατά τον D. Hilbert, Μαθηματικά. Είναι πολύ προσφυής ο παραλληλισμός της φορμαλιστικής θεωρίας με το γνωστό παιγνίδι του σκακιού. Ο παραλληλισμός αυτός πραγματοποιείται, αν αντιστοιχήσαμε τους τύπους-αξιώματα με την αρχική θέση που έχουν οι φιγούρες στο παιγνίδι, τον τρόπο παραγωγής των τύπων με τους κανόνες κινήσεων στις φιγούρες και τις αποδείξεις με τις σειρές κινήσεων του παιγνιδιού.
Όσα είπαμε πιο πάνω για τον φορμαλιστικό τρόπο δόμησης των Μαθηματικών νομίζομε ότι αποκαλύπτουν με ενάργεια τον αισθητικό χαρακτήρα της μεθόδου αυτής , μεθόδου που σε αδρές γραμμές μας δίνει μια πλήρη εποπτική εικόνα της λειτουργίας σε ένα τόσο εκτεταμένο και πολυδαίδαλο οικοδόμημα»
.........................................................................................................................................
«Εκείνο που θα μπορούσε να ερωτήσει κανείς είναι, αν υπάρχουν αντικειμενικά κριτήρια για την αξιολόγηση και την συγκριτική αποτίμηση των αισθητικών αξιών μέσα σε μια και την ίδια μαθηματική δημιουργία ή στις αισθητικές αξίες διαφόρων δημιουργιών. Η απάντηση στο ερώτημα αυτό δεν είναι καθόλου εύκολη, για να μη πούμε πως στην ουσία είναι, αρνητική. Είναι, φανερό ότι, η ύπαρξη αντικειμενικού κριτηρίου αποτίμησης των μαθηματικών αξιών ισοδυναμεί με την εύρεση κανόνων για τη δημιουργία αισθητικών αριστουργημάτων. Ούτε ακόμα είναι, δυνατή η συγχώνευση σε ένα κανόνα των διαφόρων γνωρισμάτων για καθένα χωριστά μαθηματικό επίτευγμα, που έχει, αισθητική αξία. Το βέβαιο είναι,, ότι, κ ά θ ε μαθηματικό επίτευγμα έχει, τη δική του αισθητική αξία και ότι, κατά κάποιο τρόπο, θα μπορούσε κανείς να το αντιμετωπίσει ως ένα έργο τέχνης. Στο σημείο αυτό ας μη ξεχνούμε, ότι, ο Η. Weyl παρομοιάζει την μαθηματική με την μουσική δημιουργία. Υπάρχουν αν και σπανιότερα, μαθηματικοί που αισθάνονται, την ανάγκη να προσφύγουν στον καλλιτέχνη για την αισθητική αξιολόγηση του έργου τους. Δεν θα ήταν άραγε επιθυμητό να βρίσκονταν κάποτε και καλλιτέχνες που θα συμβουλεύονταν τους μαθηματικούς για τον ίδιο λόγο;
Ένα τελευταίο ερώτημα άφορα στο κατά πόσον η συγκίνηση, η ευαισθησία και γενικά ο συναισθηματικός κόσμος του μαθηματικού, ασκεί οποιαδήποτε επίδραση στο δημιουργικό του έργο, ανάλογα με ότι, συμβαίνει, στον καλλιτέχνη. Θέλουμε να πιστεύουμε, ότι, και στο σημείο αυτό υπάρχει, αναλογία ανάμεσα στο έργο ενός καλλιτέχνη και ενός μαθηματικού, αφού άλλωστε η αγάπη και το πάθος για την επιστήμη του οδηγούν τον μαθηματικό στο δημιουργικό του έργο»
Φίλων ΒΑΣΙΛΕΙΟΥ, της Ακαδημίας Αθηνών
[πηγή: Μ.Ε., τεύχ.9 (Νέα Σειρά), εκδ. ΕΜΕ, 1978]
με εκτίμηση
Γιάννης Κερασαρίδης
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
ΣΗΜΕΙΩΜΑ 30ο [ΤΕΛΕΥΤΑΙΟ]
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΑΙΣΘΗΤΙΚΗ
Προλεγόμενα Με το σημείωμα τούτο κλείνουμε αυτόν τον φάκελο [«Για ποιο λόγο διδάσκουμε τα Μαθηματικά στα παιδιά»], όχι γιατί έχει εξαντληθεί το θέμα, αλλά γιατί υπάρχει α) μια ολόκληρη θάλασσα σχετικών θεμάτων και β) γιατί ο φιλόξενος χώρος του ιστοτόπου μας είναι πολύτιμος για τους συναδέλφους. Κλείνοντας, θεωρήσαμε πως θα ήταν μέγιστη παράλειψή μας, αν δεν παραθέταμε την άποψη του Ακαδημαϊκού Φίλωνος Βασιλείου, για τη σχέση της επιστήμης των Μαθηματικών και της αισθητικής.
το κείμενο
«Είναι δύσκολο για τους πολλούς να κατανοήσουν την ύπαρξη οποιασδήποτε συγγένειας ανάμεσα στα Μαθηματικά και την Αισθητική. Κι αυτό, γιατί ο κοινός άνθρωπος θεωρεί τα Μαθηματικά ως μια επιστήμη σκοτεινή και ψυχρή, που περισσότερο αποκρούει παρά θέλγει και που γι αυτό κάθε αισθητικό στοιχείο της είναι ξένο και απρόσιτο. Ο ίδιος ακόμα συναρτά την ύπαρξη του Ωραίου μόνο με τη Φύση και την Καλλιτεχνία. Δεν μπορεί λοιπόν να σκεφτεί με ποιό τρόπο μια τόσο έκδηλα νοητική δραστηριότητα, όπως εκείνη του μαθηματικού, είναι δυνατόν να σχετίζεται με τον συναισθηματικό κόσμο, μέσα στον οποίον πολλές φορές ο καλλιτέχνης κινείται και δημιουργεί.
Ωστόσο, αν δεν σταθεί κανείς στην απλοϊκή αυτή αντίληψη και αν ζητήσει ακόμα κι ως μη ειδικός να ερευνήσει για βαθύτερες αναλογίες, δεν θ' αργήσει να εντυπωσιαστεί από πολύ στενές ομοιότητες, που υπάρχουν στις επιφανειακά τόσο διαφορετικές λειτουργίες του μαθηματικού και του καλλιτεχνικού νου. Δεν αποκλείεται η έκπληξη να οδηγήσει ακόμα και στην ακραία άποψη, πως δηλαδή τα Μαθηματικά πρέπει κι αυτά να θεωρηθούν ως μια Καλή Τέχνη.
Οι ομοιότητες, για τις οποίες έγινε λόγος, αφορούν είτε στον τρόπο λειτουργίας του δημιουργικού νου, στις δύο εξεταζόμενες περιπτώσεις , είτε σε κοινές βασικές έννοιες που χρησιμοποιεί τόσον ο μαθηματικός όσον και ο καλλιτέχνης. Εξάλλου η θεώρηση καθ' εαυτήν οποιασδήποτε μαθηματικής δομής μαζί με την χρησιμοποιούμενη μέθοδο δόμησής της παρέχει πραγματικά μια καθαρά αισθητική απόλαυση με τη θαυμαστή αρμονία αρχιτεκτονικής και την κομψότητα στην έκθεση των θεωριών της»
............................................................................................................................................
«Μια βασική τώρα έννοια, κοινή στα Μαθηματικά και στην Καλλιτεχνία, εκτός από τις γνωστές σε όλους χ ρ υ σ ή τ ο μ ή και σ υ μ μ ε τα ρ ί α, είναι εκείνη του σ υ μ π λ έ γ μ α τ ο ς , αλλιώς ο μ ά δ α ς , που πηγάζει απ' αυτήν την έννοια της συμμετρίας. Σε ένα γεωμετρικό σχήμα συμμετρία είναι μια αμφιμονοσήμαντη απεικόνιση των σημείων του σχήματος επάνω στα ίδια αυτά σημεία με διατήρηση της απόστασής τους ανά δυο. Η πράξη της αλλεπάλληλης εφαρμογής δύο τέτοιων απεικονίσεων, που έχει ορισμένες ιδιότητες, παρέχει ένα σύστημα από απεικονίσεις. Γενίκευση του συστήματος αυτού σε οποιαδήποτε αφηρημένα στοιχεία (στη θέση απεικονίσεων) για τα οποία ορίζεται, μια μονοσήμαντη διμελής πράξη που υπακούει. σε ίδιες ιδιότητες όπως οι απεικονίσεις, αποτελεί αυτό που ονομάζουμε σύστημα συμπλεγμάτων.
Η έννοια του συμπλέγματος εισέρχεται σε κάθε σχεδόν κλάδο των σύγχρονων Μαθηματικών. Ιδιαίτερα μια από τις πιο βαθιές και ωραίες μαθηματικές θεωρίες, η λεγόμενη θεωρία του Ε. Galois , έχει τις ρίζες της στα συμπλέγματα. Στις Καλές Τέχνες, ιδιαίτερα στη Μουσική, η έννοια του συμπλέγματος παίζει επίσης σπουδαιότατο ρόλο. Έτσι, η "Τέχνη της Φούγκας" του J.S. Bach δείχνει, πόσο βαθειά εισδύουν στη μουσική σύνθεση μαθηματικές έννοιες. Άλλωστε η σημασία της επίδρασης καταφαίνεται και από το γεγονός, ότι το έργο αυτό θεωρείται ως το πιο μεγαλεπήβολο δείγμα σύνθεσης στη Μουσική της Δύσης. Δεν μπορεί φυσικά να υποστηριχθεί, ότι ο συνθέτης του υπ' όψη έργου καθοδηγείτο ενσυνείδητα από κάποια μαθηματική θεωρία. Ακριβώς όμως η σύνθεση αυτή καταδεικνύει, μια στενή συγγένεια ανάμεσα στη Μουσική και στα Μαθηματικά.
Από μουσικοκριτικές αναλύσεις της Σονάτας 15, Op.28 για πιάνο του L.van Beethoven συμπεραίνομαι ακόμα, ότι, το έργο αυτό έχει συντεθεί, φυσικά με τρόπο μη συνειδητό, απάνω σε μαθηματικά πρότυπα, συγκεκριμένα στη θεωρία των συμπλεγμάτων. Το ίδιο μπορεί να ειπωθεί και, για άλλες μουσικές
συνθέσεις, όπως για μερικά όχι τόσο γνωστά έργα του W.Α. Μozart και του J. Haydn .
Αλλά και σχετικά με την ίδια τη δομή μιας μαθηματικής θεωρίας υπάρχει υψηλή αισθητική απόλαυση, που για να τη δοκιμάσει όμως κανείς απαιτείται - όπως και στην Τέχνη - προηγούμενη καλλιέργεια αυτού που ονομάζομε μ α θ η μ α τ ι κ ό γ ο ύ σ τ ο, ανάλογο με το καλλιτεχνικό. Την αισθητική απόλαυση, στην περίπτωση μιας μαθηματικής θεωρίας, τη δίνει η τ ε λ ε ι ό τ η τ α στις αποδείξεις, η α ρ μ ο ν ί α ανάμεσα στα διάφορα μέρη και η αυστηρή α ρ χ ι τ ε κ τ ο ν ι κ ή του όλου. Στην αρμονία αυτή, τη συμμετρία και την πλήρη ισορρόπηση των μερών, αποδίδει ο Poincare την αίσθηση της κομψότητας, που χαρακτηρίζει τα Μαθηματικά.
Αναφορικά με τη μέθοδο δόμησης σημειώνουμε, ότι ένα από τα κύρια εφόδια στα Μαθηματικά είναι οι συμβολικοί τ ύ π ο ι, που αντιπροσωπεύουν αυτές τις ίδιες τις μαθηματικές ι δ έ ε ς. Ώστε, η ακολουθούμενη αξιωματική μεθοδολογία για τον χειρισμό των τύπων αυτών εμφανίζει έναν πρόσθετο τομέα, άξιο να εξεταστεί για τον αισθητικό του χαρακτήρα.
Μια από τις σύγχρονες Σχολές, που θέλει να ερμηνεύσει την ίδρυση των Μαθηματικών, είναι η "Φορμαλιστική Σχολή" που οφείλεται στον D. Hilbert . Πρόκειται για την θεώρηση εκείνη των Μαθηματικών, που τα βλέπει κανείς πρώτα ως ένα σύστημα από τύπους, χωρίς οποιαδήποτε σημασία, και από πράξεις επάνω στους τύπους αυτούς - πράξεις που εκτελούνται σύμφωνα με ορισμένους κανόνες. Στο σύστημα αυτό ξεκινά κανείς από ορισμένους τύπους-αξιώματα και απ' αυτά συνάγει, τους λοιπούς τύπους του συστήματος με βάση τις δοθείσες τυπικές πράξεις. Έπειτα η εφαρμογή μιας άλλης , εποπτικής τη φορά αυτή, θεωρίας - που φέρει το όνομα Μεταμαθηματικά-συμπληρώνει αυτό που ονομάζουμε, κατά τον D. Hilbert, Μαθηματικά. Είναι πολύ προσφυής ο παραλληλισμός της φορμαλιστικής θεωρίας με το γνωστό παιγνίδι του σκακιού. Ο παραλληλισμός αυτός πραγματοποιείται, αν αντιστοιχήσαμε τους τύπους-αξιώματα με την αρχική θέση που έχουν οι φιγούρες στο παιγνίδι, τον τρόπο παραγωγής των τύπων με τους κανόνες κινήσεων στις φιγούρες και τις αποδείξεις με τις σειρές κινήσεων του παιγνιδιού.
Όσα είπαμε πιο πάνω για τον φορμαλιστικό τρόπο δόμησης των Μαθηματικών νομίζομε ότι αποκαλύπτουν με ενάργεια τον αισθητικό χαρακτήρα της μεθόδου αυτής , μεθόδου που σε αδρές γραμμές μας δίνει μια πλήρη εποπτική εικόνα της λειτουργίας σε ένα τόσο εκτεταμένο και πολυδαίδαλο οικοδόμημα»
.........................................................................................................................................
«Εκείνο που θα μπορούσε να ερωτήσει κανείς είναι, αν υπάρχουν αντικειμενικά κριτήρια για την αξιολόγηση και την συγκριτική αποτίμηση των αισθητικών αξιών μέσα σε μια και την ίδια μαθηματική δημιουργία ή στις αισθητικές αξίες διαφόρων δημιουργιών. Η απάντηση στο ερώτημα αυτό δεν είναι καθόλου εύκολη, για να μη πούμε πως στην ουσία είναι, αρνητική. Είναι, φανερό ότι, η ύπαρξη αντικειμενικού κριτηρίου αποτίμησης των μαθηματικών αξιών ισοδυναμεί με την εύρεση κανόνων για τη δημιουργία αισθητικών αριστουργημάτων. Ούτε ακόμα είναι, δυνατή η συγχώνευση σε ένα κανόνα των διαφόρων γνωρισμάτων για καθένα χωριστά μαθηματικό επίτευγμα, που έχει, αισθητική αξία. Το βέβαιο είναι,, ότι, κ ά θ ε μαθηματικό επίτευγμα έχει, τη δική του αισθητική αξία και ότι, κατά κάποιο τρόπο, θα μπορούσε κανείς να το αντιμετωπίσει ως ένα έργο τέχνης. Στο σημείο αυτό ας μη ξεχνούμε, ότι, ο Η. Weyl παρομοιάζει την μαθηματική με την μουσική δημιουργία. Υπάρχουν αν και σπανιότερα, μαθηματικοί που αισθάνονται, την ανάγκη να προσφύγουν στον καλλιτέχνη για την αισθητική αξιολόγηση του έργου τους. Δεν θα ήταν άραγε επιθυμητό να βρίσκονταν κάποτε και καλλιτέχνες που θα συμβουλεύονταν τους μαθηματικούς για τον ίδιο λόγο;
Ένα τελευταίο ερώτημα άφορα στο κατά πόσον η συγκίνηση, η ευαισθησία και γενικά ο συναισθηματικός κόσμος του μαθηματικού, ασκεί οποιαδήποτε επίδραση στο δημιουργικό του έργο, ανάλογα με ότι, συμβαίνει, στον καλλιτέχνη. Θέλουμε να πιστεύουμε, ότι, και στο σημείο αυτό υπάρχει, αναλογία ανάμεσα στο έργο ενός καλλιτέχνη και ενός μαθηματικού, αφού άλλωστε η αγάπη και το πάθος για την επιστήμη του οδηγούν τον μαθηματικό στο δημιουργικό του έργο»
Φίλων ΒΑΣΙΛΕΙΟΥ, της Ακαδημίας Αθηνών
[πηγή: Μ.Ε., τεύχ.9 (Νέα Σειρά), εκδ. ΕΜΕ, 1978]
με εκτίμηση
Γιάννης Κερασαρίδης
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΑΙΣΘΗΤΙΚΗ
Προλεγόμενα Με το σημείωμα τούτο κλείνουμε αυτόν τον φάκελο [«Για ποιο λόγο διδάσκουμε τα Μαθηματικά στα παιδιά»], όχι γιατί έχει εξαντληθεί το θέμα, αλλά γιατί υπάρχει α) μια ολόκληρη θάλασσα σχετικών θεμάτων και β) γιατί ο φιλόξενος χώρος του ιστοτόπου μας είναι πολύτιμος για τους συναδέλφους. Κλείνοντας, θεωρήσαμε πως θα ήταν μέγιστη παράλειψή μας, αν δεν παραθέταμε την άποψη του Ακαδημαϊκού Φίλωνος Βασιλείου, για τη σχέση της επιστήμης των Μαθηματικών και της αισθητικής.
το κείμενο
«Είναι δύσκολο για τους πολλούς να κατανοήσουν την ύπαρξη οποιασδήποτε συγγένειας ανάμεσα στα Μαθηματικά και την Αισθητική. Κι αυτό, γιατί ο κοινός άνθρωπος θεωρεί τα Μαθηματικά ως μια επιστήμη σκοτεινή και ψυχρή, που περισσότερο αποκρούει παρά θέλγει και που γι αυτό κάθε αισθητικό στοιχείο της είναι ξένο και απρόσιτο. Ο ίδιος ακόμα συναρτά την ύπαρξη του Ωραίου μόνο με τη Φύση και την Καλλιτεχνία. Δεν μπορεί λοιπόν να σκεφτεί με ποιό τρόπο μια τόσο έκδηλα νοητική δραστηριότητα, όπως εκείνη του μαθηματικού, είναι δυνατόν να σχετίζεται με τον συναισθηματικό κόσμο, μέσα στον οποίον πολλές φορές ο καλλιτέχνης κινείται και δημιουργεί.
Ωστόσο, αν δεν σταθεί κανείς στην απλοϊκή αυτή αντίληψη και αν ζητήσει ακόμα κι ως μη ειδικός να ερευνήσει για βαθύτερες αναλογίες, δεν θ' αργήσει να εντυπωσιαστεί από πολύ στενές ομοιότητες, που υπάρχουν στις επιφανειακά τόσο διαφορετικές λειτουργίες του μαθηματικού και του καλλιτεχνικού νου. Δεν αποκλείεται η έκπληξη να οδηγήσει ακόμα και στην ακραία άποψη, πως δηλαδή τα Μαθηματικά πρέπει κι αυτά να θεωρηθούν ως μια Καλή Τέχνη.
Οι ομοιότητες, για τις οποίες έγινε λόγος, αφορούν είτε στον τρόπο λειτουργίας του δημιουργικού νου, στις δύο εξεταζόμενες περιπτώσεις , είτε σε κοινές βασικές έννοιες που χρησιμοποιεί τόσον ο μαθηματικός όσον και ο καλλιτέχνης. Εξάλλου η θεώρηση καθ' εαυτήν οποιασδήποτε μαθηματικής δομής μαζί με την χρησιμοποιούμενη μέθοδο δόμησής της παρέχει πραγματικά μια καθαρά αισθητική απόλαυση με τη θαυμαστή αρμονία αρχιτεκτονικής και την κομψότητα στην έκθεση των θεωριών της»
............................................................................................................................................
«Μια βασική τώρα έννοια, κοινή στα Μαθηματικά και στην Καλλιτεχνία, εκτός από τις γνωστές σε όλους χ ρ υ σ ή τ ο μ ή και σ υ μ μ ε τα ρ ί α, είναι εκείνη του σ υ μ π λ έ γ μ α τ ο ς , αλλιώς ο μ ά δ α ς , που πηγάζει απ' αυτήν την έννοια της συμμετρίας. Σε ένα γεωμετρικό σχήμα συμμετρία είναι μια αμφιμονοσήμαντη απεικόνιση των σημείων του σχήματος επάνω στα ίδια αυτά σημεία με διατήρηση της απόστασής τους ανά δυο. Η πράξη της αλλεπάλληλης εφαρμογής δύο τέτοιων απεικονίσεων, που έχει ορισμένες ιδιότητες, παρέχει ένα σύστημα από απεικονίσεις. Γενίκευση του συστήματος αυτού σε οποιαδήποτε αφηρημένα στοιχεία (στη θέση απεικονίσεων) για τα οποία ορίζεται, μια μονοσήμαντη διμελής πράξη που υπακούει. σε ίδιες ιδιότητες όπως οι απεικονίσεις, αποτελεί αυτό που ονομάζουμε σύστημα συμπλεγμάτων.
Η έννοια του συμπλέγματος εισέρχεται σε κάθε σχεδόν κλάδο των σύγχρονων Μαθηματικών. Ιδιαίτερα μια από τις πιο βαθιές και ωραίες μαθηματικές θεωρίες, η λεγόμενη θεωρία του Ε. Galois , έχει τις ρίζες της στα συμπλέγματα. Στις Καλές Τέχνες, ιδιαίτερα στη Μουσική, η έννοια του συμπλέγματος παίζει επίσης σπουδαιότατο ρόλο. Έτσι, η "Τέχνη της Φούγκας" του J.S. Bach δείχνει, πόσο βαθειά εισδύουν στη μουσική σύνθεση μαθηματικές έννοιες. Άλλωστε η σημασία της επίδρασης καταφαίνεται και από το γεγονός, ότι το έργο αυτό θεωρείται ως το πιο μεγαλεπήβολο δείγμα σύνθεσης στη Μουσική της Δύσης. Δεν μπορεί φυσικά να υποστηριχθεί, ότι ο συνθέτης του υπ' όψη έργου καθοδηγείτο ενσυνείδητα από κάποια μαθηματική θεωρία. Ακριβώς όμως η σύνθεση αυτή καταδεικνύει, μια στενή συγγένεια ανάμεσα στη Μουσική και στα Μαθηματικά.
Από μουσικοκριτικές αναλύσεις της Σονάτας 15, Op.28 για πιάνο του L.van Beethoven συμπεραίνομαι ακόμα, ότι, το έργο αυτό έχει συντεθεί, φυσικά με τρόπο μη συνειδητό, απάνω σε μαθηματικά πρότυπα, συγκεκριμένα στη θεωρία των συμπλεγμάτων. Το ίδιο μπορεί να ειπωθεί και, για άλλες μουσικές
συνθέσεις, όπως για μερικά όχι τόσο γνωστά έργα του W.Α. Μozart και του J. Haydn .
Αλλά και σχετικά με την ίδια τη δομή μιας μαθηματικής θεωρίας υπάρχει υψηλή αισθητική απόλαυση, που για να τη δοκιμάσει όμως κανείς απαιτείται - όπως και στην Τέχνη - προηγούμενη καλλιέργεια αυτού που ονομάζομε μ α θ η μ α τ ι κ ό γ ο ύ σ τ ο, ανάλογο με το καλλιτεχνικό. Την αισθητική απόλαυση, στην περίπτωση μιας μαθηματικής θεωρίας, τη δίνει η τ ε λ ε ι ό τ η τ α στις αποδείξεις, η α ρ μ ο ν ί α ανάμεσα στα διάφορα μέρη και η αυστηρή α ρ χ ι τ ε κ τ ο ν ι κ ή του όλου. Στην αρμονία αυτή, τη συμμετρία και την πλήρη ισορρόπηση των μερών, αποδίδει ο Poincare την αίσθηση της κομψότητας, που χαρακτηρίζει τα Μαθηματικά.
Αναφορικά με τη μέθοδο δόμησης σημειώνουμε, ότι ένα από τα κύρια εφόδια στα Μαθηματικά είναι οι συμβολικοί τ ύ π ο ι, που αντιπροσωπεύουν αυτές τις ίδιες τις μαθηματικές ι δ έ ε ς. Ώστε, η ακολουθούμενη αξιωματική μεθοδολογία για τον χειρισμό των τύπων αυτών εμφανίζει έναν πρόσθετο τομέα, άξιο να εξεταστεί για τον αισθητικό του χαρακτήρα.
Μια από τις σύγχρονες Σχολές, που θέλει να ερμηνεύσει την ίδρυση των Μαθηματικών, είναι η "Φορμαλιστική Σχολή" που οφείλεται στον D. Hilbert . Πρόκειται για την θεώρηση εκείνη των Μαθηματικών, που τα βλέπει κανείς πρώτα ως ένα σύστημα από τύπους, χωρίς οποιαδήποτε σημασία, και από πράξεις επάνω στους τύπους αυτούς - πράξεις που εκτελούνται σύμφωνα με ορισμένους κανόνες. Στο σύστημα αυτό ξεκινά κανείς από ορισμένους τύπους-αξιώματα και απ' αυτά συνάγει, τους λοιπούς τύπους του συστήματος με βάση τις δοθείσες τυπικές πράξεις. Έπειτα η εφαρμογή μιας άλλης , εποπτικής τη φορά αυτή, θεωρίας - που φέρει το όνομα Μεταμαθηματικά-συμπληρώνει αυτό που ονομάζουμε, κατά τον D. Hilbert, Μαθηματικά. Είναι πολύ προσφυής ο παραλληλισμός της φορμαλιστικής θεωρίας με το γνωστό παιγνίδι του σκακιού. Ο παραλληλισμός αυτός πραγματοποιείται, αν αντιστοιχήσαμε τους τύπους-αξιώματα με την αρχική θέση που έχουν οι φιγούρες στο παιγνίδι, τον τρόπο παραγωγής των τύπων με τους κανόνες κινήσεων στις φιγούρες και τις αποδείξεις με τις σειρές κινήσεων του παιγνιδιού.
Όσα είπαμε πιο πάνω για τον φορμαλιστικό τρόπο δόμησης των Μαθηματικών νομίζομε ότι αποκαλύπτουν με ενάργεια τον αισθητικό χαρακτήρα της μεθόδου αυτής , μεθόδου που σε αδρές γραμμές μας δίνει μια πλήρη εποπτική εικόνα της λειτουργίας σε ένα τόσο εκτεταμένο και πολυδαίδαλο οικοδόμημα»
.........................................................................................................................................
«Εκείνο που θα μπορούσε να ερωτήσει κανείς είναι, αν υπάρχουν αντικειμενικά κριτήρια για την αξιολόγηση και την συγκριτική αποτίμηση των αισθητικών αξιών μέσα σε μια και την ίδια μαθηματική δημιουργία ή στις αισθητικές αξίες διαφόρων δημιουργιών. Η απάντηση στο ερώτημα αυτό δεν είναι καθόλου εύκολη, για να μη πούμε πως στην ουσία είναι, αρνητική. Είναι, φανερό ότι, η ύπαρξη αντικειμενικού κριτηρίου αποτίμησης των μαθηματικών αξιών ισοδυναμεί με την εύρεση κανόνων για τη δημιουργία αισθητικών αριστουργημάτων. Ούτε ακόμα είναι, δυνατή η συγχώνευση σε ένα κανόνα των διαφόρων γνωρισμάτων για καθένα χωριστά μαθηματικό επίτευγμα, που έχει, αισθητική αξία. Το βέβαιο είναι,, ότι, κ ά θ ε μαθηματικό επίτευγμα έχει, τη δική του αισθητική αξία και ότι, κατά κάποιο τρόπο, θα μπορούσε κανείς να το αντιμετωπίσει ως ένα έργο τέχνης. Στο σημείο αυτό ας μη ξεχνούμε, ότι, ο Η. Weyl παρομοιάζει την μαθηματική με την μουσική δημιουργία. Υπάρχουν αν και σπανιότερα, μαθηματικοί που αισθάνονται, την ανάγκη να προσφύγουν στον καλλιτέχνη για την αισθητική αξιολόγηση του έργου τους. Δεν θα ήταν άραγε επιθυμητό να βρίσκονταν κάποτε και καλλιτέχνες που θα συμβουλεύονταν τους μαθηματικούς για τον ίδιο λόγο;
Ένα τελευταίο ερώτημα άφορα στο κατά πόσον η συγκίνηση, η ευαισθησία και γενικά ο συναισθηματικός κόσμος του μαθηματικού, ασκεί οποιαδήποτε επίδραση στο δημιουργικό του έργο, ανάλογα με ότι, συμβαίνει, στον καλλιτέχνη. Θέλουμε να πιστεύουμε, ότι, και στο σημείο αυτό υπάρχει, αναλογία ανάμεσα στο έργο ενός καλλιτέχνη και ενός μαθηματικού, αφού άλλωστε η αγάπη και το πάθος για την επιστήμη του οδηγούν τον μαθηματικό στο δημιουργικό του έργο»
Φίλων ΒΑΣΙΛΕΙΟΥ, της Ακαδημίας Αθηνών
[πηγή: Μ.Ε., τεύχ.9 (Νέα Σειρά), εκδ. ΕΜΕ, 1978]
με εκτίμηση
Γιάννης Κερασαρίδης
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
Γιάννη,σου οφείλουμε ένα μεγάλο ΕΥΧΑΡΙΣΤΩ για την πολύ όμορφη εργασία που μας παρουσίασες. Ο καθένας από εμάς μπορεί να χρησιμοποιήσει μέρος της δουλειάς σου και να την παρουσιάσει και στους μαθητές. Είναι μια πλήρης απάντηση στο ερώτημα:
¨Γιατί διδάσκουμε τα μαθηματικά"
Να είσαι πάντα καλά και να μας προσφέρεις έτσι απλόχερα την γνώση και την εμπειρία σου.
¨Γιατί διδάσκουμε τα μαθηματικά"
Να είσαι πάντα καλά και να μας προσφέρεις έτσι απλόχερα την γνώση και την εμπειρία σου.
Re: Γιά ποιό λόγο διδάσκουμε τα Μαθηματικά στα παιδιά;
Φίλε Δημήτρη,
σε ευχαριστώ για τα καλά σου λόγια κι αυτό με ικανοποιεί ψυχικά. Όσον αφορά την άποψή σου να τα χρησιμοποιήσεις στο Σχολείο και βέβαια μπορείς. Η γνώση είναι "κοινωνικό" αγαθό και σαν τέτοιο δίνει το δικαίωμα σε κάθε άνθρωπο να έχει πρόσβαση σ’ αυτήν.
Δημήτρη,
με την ευκαιρία αυτή μπαίνω στον πειρασμό να παραθέσω τρεις υπομνήσεις:
α) Όταν ρωτήθηκε ο Η. Poincare γιατί δεν δημοσιοποίησε τις απόψεις του για την Σχετικότητα (είχε προηγηθεί ο Einstein με τη δική του Σχετικότητα), ο μεγάλος διανοητής απάντησε: «δεν αρκεί να ξέρεις κάτι˙ αν δεν το βγάλεις προς τα έξω, ισοδυναμεί σαν μη το ήξερες»
β) όταν ο Ραμσή Β΄ έγινε Φαραώ, ζήτησε από το ιερατείο να του "παραδώσουν" όλη τη γνώση τους, μια κι αυτή (που τους έδινε τη δύναμή τους), τους την εμπιστεύθηκε σ’ αυτούς, ο πατέρας του ο θεός Ήλιος. Το ιερατείο μπρος στον κίνδυνο να φύγει η δύναμη απ’ τα χέρια τους, φρόντισαν κι "έστειλαν" τον Ραμσή Β΄ να συναντήσει αυτοπροσώπως τον πατέρα του…
γ) δεν πρέπει να ξεχνάμε πως οι θεοί τιμώρησαν τον Προμηθέα επειδή μετέφερε στους ανθρώπου γνώση
με εκτίμηση
Γιάννης Κερασαρίδης
σε ευχαριστώ για τα καλά σου λόγια κι αυτό με ικανοποιεί ψυχικά. Όσον αφορά την άποψή σου να τα χρησιμοποιήσεις στο Σχολείο και βέβαια μπορείς. Η γνώση είναι "κοινωνικό" αγαθό και σαν τέτοιο δίνει το δικαίωμα σε κάθε άνθρωπο να έχει πρόσβαση σ’ αυτήν.
Δημήτρη,
με την ευκαιρία αυτή μπαίνω στον πειρασμό να παραθέσω τρεις υπομνήσεις:
α) Όταν ρωτήθηκε ο Η. Poincare γιατί δεν δημοσιοποίησε τις απόψεις του για την Σχετικότητα (είχε προηγηθεί ο Einstein με τη δική του Σχετικότητα), ο μεγάλος διανοητής απάντησε: «δεν αρκεί να ξέρεις κάτι˙ αν δεν το βγάλεις προς τα έξω, ισοδυναμεί σαν μη το ήξερες»
β) όταν ο Ραμσή Β΄ έγινε Φαραώ, ζήτησε από το ιερατείο να του "παραδώσουν" όλη τη γνώση τους, μια κι αυτή (που τους έδινε τη δύναμή τους), τους την εμπιστεύθηκε σ’ αυτούς, ο πατέρας του ο θεός Ήλιος. Το ιερατείο μπρος στον κίνδυνο να φύγει η δύναμη απ’ τα χέρια τους, φρόντισαν κι "έστειλαν" τον Ραμσή Β΄ να συναντήσει αυτοπροσώπως τον πατέρα του…
γ) δεν πρέπει να ξεχνάμε πως οι θεοί τιμώρησαν τον Προμηθέα επειδή μετέφερε στους ανθρώπου γνώση
με εκτίμηση
Γιάννης Κερασαρίδης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες
