
Μέγιστος Κοινός Διαιρέτης
Συντονιστής: spyros
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Μέγιστος Κοινός Διαιρέτης
Το αποτέλεσμα είναι προφανές για  οπότε θα υποθέσουμε ότι
οπότε θα υποθέσουμε ότι  .
.
Έστω ότι . Τότε
. Τότε 
Άρα
Έστω όπου
όπου  . Τότε
. Τότε 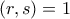 και παίρνουμε
και παίρνουμε 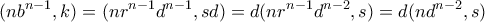
Έχουμε επίσης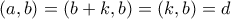 άρα
άρα

οπότε έχουμε το ζητούμενο.
 οπότε θα υποθέσουμε ότι
οπότε θα υποθέσουμε ότι  .
.Έστω ότι
 . Τότε
. Τότε 
Άρα

Έστω
 όπου
όπου  . Τότε
. Τότε 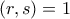 και παίρνουμε
και παίρνουμε 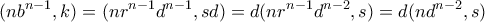
Έχουμε επίσης
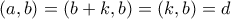 άρα
άρα
οπότε έχουμε το ζητούμενο.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες
