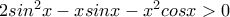 για
για  .
.[Η προέλευση θα αποκαλυφθεί αργότερα.]
Συντονιστής: nsmavrogiannis
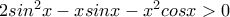 για
για  .
.Καλημέρα Γιώργο.
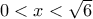 .
. οι ανισότητες (βγαίνουν και με σχολική ύλη)
οι ανισότητες (βγαίνουν και με σχολική ύλη)


Σταύρο καλησπέρα, και σ' ευχαριστώ για την ενασχόληση. Οι γνωστές-άγνωστες ανισότητες είναι πράγματι ο εύκολος δρόμος, που προτιμώ όμως να αποφεύγω όταν αυτό είναι δυνατόν ... ιδίως ύστερα από το 'συμβάν' στις περυσινές πανελλαδικέςΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Μάιος 28, 2019 9:47 amΚαλημέρα Γιώργο.
Θα την απαντήσω σαν να ήταν στο φάκελλο Ανάλυση.
Επίσης ισχύει τουλάχιστον για.
Είναι γνωστές γιαοι ανισότητες (βγαίνουν και με σχολική ύλη)
Αν τις εφαρμόσουμε τότε η αριστερή παράσταση στην ανισότητα είναι
μεγαλύτερη από

Καλησπέρα Γιώργο.gbaloglou έγραψε: ↑Τετ Μάιος 29, 2019 4:46 pmΣταύρο καλησπέρα, και σ' ευχαριστώ για την ενασχόληση. Οι γνωστές-άγνωστες ανισότητες είναι πράγματι ο εύκολος δρόμος, που προτιμώ όμως να αποφεύγω όταν αυτό είναι δυνατόν ... ιδίως ύστερα από το 'συμβάν' στις περυσινές πανελλαδικέςΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Μάιος 28, 2019 9:47 amΚαλημέρα Γιώργο.
Θα την απαντήσω σαν να ήταν στο φάκελλο Ανάλυση.
Επίσης ισχύει τουλάχιστον για.
Είναι γνωστές γιαοι ανισότητες (βγαίνουν και με σχολική ύλη)
Αν τις εφαρμόσουμε τότε η αριστερή παράσταση στην ανισότητα είναι
μεγαλύτερη από

Θα ήταν ίσως επίσης καλύτερη ιδέα να έβαζα την άσκηση στον Φάκελλο Καθηγητή -- Γενικά ... αλλά μάλλον δεν βγαίνει με 'ανισοτική παραγώγιση' ... οπότε την έβαλα εδώ, υπαινισσόμενος ότι βγαίνει και με (πολύ) παραδοσιακά μέσα, χωρίς Γ' Λυκείου...
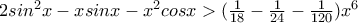
Τα παρακάτω περιέχουν σοβαρό ΛΑΘΟΣ


 (1)
(1)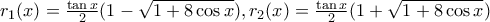



 για
για  έχει γεωμετρική απόδειξη
έχει γεωμετρική απόδειξη 
Λοιπόν, ας πάρουμε τα πράγματα από την αρχή: η παρούσα συζήτηση οφείλεται σε πρόβλημα του Βασίλη Μαυροφρύδη στο Μαθηματικό Εργαστήρι (ΦΒ), που ζητούσε να αποδειχθεί ότι είναι αύξουσα η
 στο
στο  , πρόβλημα που μέσω παραγώγισης ανάγεται στην αρνητικότητα της
, πρόβλημα που μέσω παραγώγισης ανάγεται στην αρνητικότητα της  και, μέσω δεύτερης παραγώγισης, στην αρνητικότητα της
και, μέσω δεύτερης παραγώγισης, στην αρνητικότητα της  ... την οποία απέδειξα και με προσεγγίσεις Taylor (ακριβώς όπως ο Σταύρος παραπάνω) και τριωνυμικά με χρήση των παλιών αγαπημένων τύπων
... την οποία απέδειξα και με προσεγγίσεις Taylor (ακριβώς όπως ο Σταύρος παραπάνω) και τριωνυμικά με χρήση των παλιών αγαπημένων τύπων 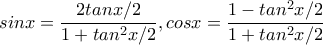 (όπως περίπου ο Σταύρος δηλαδή).
(όπως περίπου ο Σταύρος δηλαδή). :
: , που 'ανάγεται' εύκολα ('μέσω'
, που 'ανάγεται' εύκολα ('μέσω'  για
για  ) στην ΜΗ ΙΣΧΥΟΥΣΑ
) στην ΜΗ ΙΣΧΥΟΥΣΑ  .
. , όπου
, όπου  , που 'ανάγεται' εύκολα ('μέσω'
, που 'ανάγεται' εύκολα ('μέσω'  για
για  ) στην ΜΗ ΙΣΧΥΟΥΣΑ
) στην ΜΗ ΙΣΧΥΟΥΣΑ  .
. :
: , που 'ανάγεται' εύκολα στην ΜΗ ΙΣΧΥΟΥΣΑ
, που 'ανάγεται' εύκολα στην ΜΗ ΙΣΧΥΟΥΣΑ  .
. , που 'ανάγεται' εύκολα στην ΜΗ ΙΣΧΥΟΥΣΑ
, που 'ανάγεται' εύκολα στην ΜΗ ΙΣΧΥΟΥΣΑ  .
. .]
.]Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες