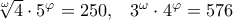
(Πολυτ. 1930)
Το πήρα από ένα παλιό βιβλίο. Αργότερα μπορούμε να δούμε και την λύση που προτείνει ο συγγραφέας.
Συντονιστής: nsmavrogiannis
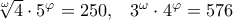
Στα σχολικά μου χρόνια, το πάλαι ποτέ, τέτοιες ασκήσεις ήταν στο ρεπερτόριο της στάνταρ διδασκαλίας.nsmavrogiannis έγραψε: ↑Τετ Απρ 26, 2023 10:19 pmΝα λυθεί το σύστημα
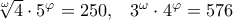
(Πολυτ. 1930)
Το πήρα από ένα παλιό βιβλίο.
system01.png
Αργότερα μπορούμε να δούμε και την λύση που προτείνει ο συγγραφέας.
 και κάναμε εκτενή χρήση λογαριθμικών πινάκων) έχουμε
και κάναμε εκτενή χρήση λογαριθμικών πινάκων) έχουμε 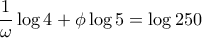 και
και 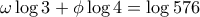
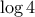 , την δεύτερη επί
, την δεύτερη επί 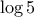 και αφαιρούμε. Θα προκύψει
και αφαιρούμε. Θα προκύψει 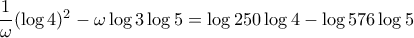
 , αντικαθιστούμε στην πρώτη, και λοιπά. Αφήνω τις πράξεις.
, αντικαθιστούμε στην πρώτη, και λοιπά. Αφήνω τις πράξεις.Τοnsmavrogiannis έγραψε: ↑Τετ Απρ 26, 2023 10:19 pmΝα λυθεί το σύστημα
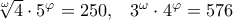
(Πολυτ. 1930)
Το πήρα από ένα παλιό βιβλίο.
system01.png
Αργότερα μπορούμε να δούμε και την λύση που προτείνει ο συγγραφέας.
 είναι πραγματικός αριθμός και
είναι πραγματικός αριθμός και 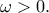 Η πρώτη εξίσωση, υψώνοντας στην
Η πρώτη εξίσωση, υψώνοντας στην  γράφεται:
γράφεται: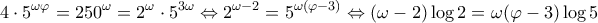
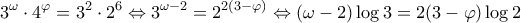
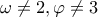 και διαιρώ κατά μέλη.
και διαιρώ κατά μέλη.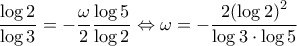 που είναι άτοπο, αφού
που είναι άτοπο, αφού 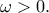
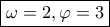 που επαληθεύει και τις δύο εξισώσεις του συστήματος.
που επαληθεύει και τις δύο εξισώσεις του συστήματος.![\sqrt[n]{a} \sqrt[n]{a}](/forum/ext/geomar/texintegr/latexrender/pictures/fc5a3fbda2d8c1b1f371fd66c5c718c0.png) .
.![\sqrt[-n]{a}=\frac{1}{ \sqrt[n]{a}} \sqrt[-n]{a}=\frac{1}{ \sqrt[n]{a}}](/forum/ext/geomar/texintegr/latexrender/pictures/560c2f48eb4e343bc029ed32ccbd3732.png) υπάρχει άλλο ένα ζευγάρι νομίζω.
υπάρχει άλλο ένα ζευγάρι νομίζω.Christos.N έγραψε: ↑Παρ Απρ 28, 2023 6:32 pmΜήπως γνωρίζετε τι ορισμό έδιναν εκείνη την εποχή στο συμβολισμό.
Γιατί αν δεχτούμε ότιυπάρχει άλλο ένα ζευγάρι νομίζω.
 (νιοστή) ρίζα, ένθα
(νιοστή) ρίζα, ένθα  φυσικός αριθμός, αριθμού τινός
φυσικός αριθμός, αριθμού τινός  , ο αριθμός ο οποίος υψούμενος εις την
, ο αριθμός ο οποίος υψούμενος εις την  (νιοστήν) δύναμιν, δίδει τον αριθμόν
(νιοστήν) δύναμιν, δίδει τον αριθμόν 
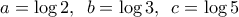
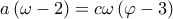
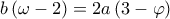
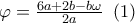
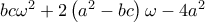
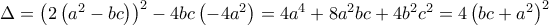
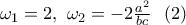
 μας δίνουν
μας δίνουν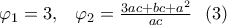
 .
.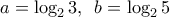 θα έχουμε τις εξισώσεις:
θα έχουμε τις εξισώσεις: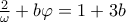
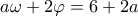
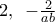 για το
για το  με αντίστοιχες τιμές για το
με αντίστοιχες τιμές για το  τις
τις 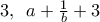 .
. ακεραίους και αξιοποιεί το μονοσήμαντο της ανάλυσης σε γινόμενο πρώτων παραγόντων.
Διαπίστωσα ότι η ίδια λύση παρατίθεται και στον τρίτο τόμο της Μεγάλης Άλγεβρας του Αρ. Πάλλα έκδοση του 1946.
ακεραίους και αξιοποιεί το μονοσήμαντο της ανάλυσης σε γινόμενο πρώτων παραγόντων.
Διαπίστωσα ότι η ίδια λύση παρατίθεται και στον τρίτο τόμο της Μεγάλης Άλγεβρας του Αρ. Πάλλα έκδοση του 1946.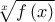 οι συγγραφείς εκείνης της εποχής. Κοιτώντας κάποιες Άλγεβρες (Παπανικολάου, Τόγκας, Μπαρπαστάθης, Πάλλας) δεν κατόρθωσα να βρω κάποιο σαφή ορισμό. Ορίζουν το σύμβολο
οι συγγραφείς εκείνης της εποχής. Κοιτώντας κάποιες Άλγεβρες (Παπανικολάου, Τόγκας, Μπαρπαστάθης, Πάλλας) δεν κατόρθωσα να βρω κάποιο σαφή ορισμό. Ορίζουν το σύμβολο 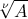 για
για  θετικό ακέραιο (όπως αναφέρει ο Γιώργος στο 5#) και μετά κάπου στις εκθετικές εξισώσεις εμφανίζεται άγνωστος και στο δείκτη της ρίζας. Ο Παπανικολάου στην αμέσως προηγούμενη άσκηση δέχεται και τιμή
θετικό ακέραιο (όπως αναφέρει ο Γιώργος στο 5#) και μετά κάπου στις εκθετικές εξισώσεις εμφανίζεται άγνωστος και στο δείκτη της ρίζας. Ο Παπανικολάου στην αμέσως προηγούμενη άσκηση δέχεται και τιμή  για τoν δείκτη.
για τoν δείκτη.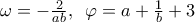 , όπου
, όπου 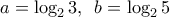
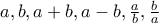 δεν βλέπω (για την ώρα ; ) κάτι για τους
δεν βλέπω (για την ώρα ; ) κάτι για τους 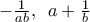 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης