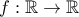 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 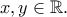
Συντονιστής: emouroukos
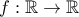 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 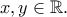
Η (1) γιαsocrates έγραψε:Να προσδιορίσετε όλες τις συνεχείς συναρτήσειςτέτοιες ώστε (1)
για κάθε
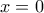 δίνει
δίνει  , άρα η
, άρα η  είναι 1-1 και επί.
είναι 1-1 και επί. θα είναι γνησίως μονότονη.
θα είναι γνησίως μονότονη. ώστε
ώστε 
 δίνει
δίνει  (2)
(2)
 είναι γνησίως φθίνουσα, τότε από τη σχέση
είναι γνησίως φθίνουσα, τότε από τη σχέση  παίρνουμε
παίρνουμε (3) και επειδή
(3) και επειδή  (4) με πολλαπλασιασμό κατά μέλη των (3) και (4) έχουμε
(4) με πολλαπλασιασμό κατά μέλη των (3) και (4) έχουμε  , αντίφαση
, αντίφαση με
με  , τότε
, τότε  , άτοπο.
, άτοπο. με
με  , τότε
, τότε  , άτοπο.
, άτοπο. , που αληθεύει την συναρτησιακή εξίσωση.
, που αληθεύει την συναρτησιακή εξίσωση. .
. και
και  η δοσμένη δίνει
η δοσμένη δίνει  , οπότε η
, οπότε η  είναι επί. Ειδικότερα, υπάρχει
είναι επί. Ειδικότερα, υπάρχει  με
με  . Με
. Με  η αρχική δίνει
η αρχική δίνει  , οπότε
, οπότε  , και αφού
, και αφού  , προκύπτει ότι
, προκύπτει ότι  , όπως θέλαμε
, όπως θέλαμε 
 είναι ενέλιξη.
είναι ενέλιξη. στην δοσμένη
στην δοσμένη 
 .
. στην δοσμένη
στην δοσμένη 
 είναι Cauchy.
είναι Cauchy. υπάρχει
υπάρχει  ώστε
ώστε  . Αφού η
. Αφού η  είναι επί, υπάρχει
είναι επί, υπάρχει  ώστε
ώστε  . Για αυτό το
. Για αυτό το  , είναι
, είναι  , οπότε
, οπότε  , όπως θέλαμε. Τώρα, για κάθε
, όπως θέλαμε. Τώρα, για κάθε  , αν ο
, αν ο  είναι τέτοιος ώστε
είναι τέτοιος ώστε  , με
, με  και
και  η αρχική δίνει
η αρχική δίνει  , άρα πράγματι η
, άρα πράγματι η  είναι Cauchy
είναι Cauchy 
 στην
στην  προκύπτει ότι
προκύπτει ότι  και με
και με  στην
στην  έχουμε ότι
έχουμε ότι  , οπότε
, οπότε  . Επίσης, με
. Επίσης, με  στην ίδια σχέση, έχουμε (χρησιμοποιούμε ότι η
στην ίδια σχέση, έχουμε (χρησιμοποιούμε ότι η  είναι Cauchy)
είναι Cauchy) , άρα
, άρα 
 .
. και κάνοντας τις απλοποιήσεις, προκύπτει ότι
και κάνοντας τις απλοποιήσεις, προκύπτει ότι  . Με
. Με  σε αυτήν, έχουμε (χρησιμοποιούμε ότι η
σε αυτήν, έχουμε (χρησιμοποιούμε ότι η  είναι Cauchy)
είναι Cauchy)
 , και αφού
, και αφού , προκύπτει ότι
, προκύπτει ότι  , το οποίο δίνει ότι
, το οποίο δίνει ότι  .
. .
. τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης