Έστω οι θετικοί πραγματικοί αριθμοί
 ,
,  με
με  και τα
και τα 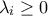 ,
,  τέτοια ώστε
τέτοια ώστε  . Να προσδιορίσετε το:
. Να προσδιορίσετε το: 
Φιλικά,
Μάριος
Συντονιστής: emouroukos
 ,
,  με
με  και τα
και τα 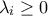 ,
,  τέτοια ώστε
τέτοια ώστε  . Να προσδιορίσετε το:
. Να προσδιορίσετε το: 




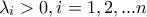
 αγνώστους
αγνώστους 
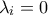
 στο
στο  και κάνοντας τα ίδια φτάνουμε στο
και κάνοντας τα ίδια φτάνουμε στο  .
. .
. (πανεύκολο)
(πανεύκολο) και
και  συνάρτηση
συνάρτηση στο
στο  ώστε να μεγιστοποιείτε το
ώστε να μεγιστοποιείτε το 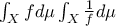
Μάριε,M.S.Vovos έγραψε: Δύσκολη άσκηση τελικά. Δεν μου πήγε καν το μυαλό για πολλαπλασιαστές Lagrange.
 μπορεί να προκύψει η ανισότητα του Kantorovich.
μπορεί να προκύψει η ανισότητα του Kantorovich.

 η εξίσωση της ευθείας που συνδέει τα
η εξίσωση της ευθείας που συνδέει τα  και
και 

 με μάζες
με μάζες 
 και
και 


 είναι τριώνυμο και η τιμή του στα
είναι τριώνυμο και η τιμή του στα 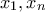 είναι
είναι 


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες