Θεωρούμε
 2 φορές παραγωγίσιμη για την οποία ισχύει
2 φορές παραγωγίσιμη για την οποία ισχύει  ,
, 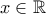
1)Δείξτε ότι οι ρίζες της
 δεν έχουν σημείο συσσώρευσης.
δεν έχουν σημείο συσσώρευσης.Δηλαδή αν
 τότε υπάρχει
τότε υπάρχει  ώστε
ώστε 
2)Αν
 δύο διαδοχικές ρίζες και
δύο διαδοχικές ρίζες και 
τότε

3)Αν
 δύο διαδοχικές ρίζες και
δύο διαδοχικές ρίζες και 
τότε

Συντονιστής: emouroukos
 2 φορές παραγωγίσιμη για την οποία ισχύει
2 φορές παραγωγίσιμη για την οποία ισχύει  ,
, 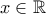
 δεν έχουν σημείο συσσώρευσης.
δεν έχουν σημείο συσσώρευσης. τότε υπάρχει
τότε υπάρχει  ώστε
ώστε 
 δύο διαδοχικές ρίζες και
δύο διαδοχικές ρίζες και 

 δύο διαδοχικές ρίζες και
δύο διαδοχικές ρίζες και 

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Ιαν 19, 2018 7:59 pmΜε αφορμή το viewtopic.php?f=61&t=60831
Θεωρούμε2 φορές παραγωγίσιμη για την οποία ισχύει
,
1)Δείξτε ότι οι ρίζες τηςδεν έχουν σημείο συσσώρευσης.
Δηλαδή αντότε υπάρχει
ώστε
2)Ανδύο διαδοχικές ρίζες και
τότε
3)Ανδύο διαδοχικές ρίζες και
τότε
 και
και 




![\Leftrightarrow [f'(x)sin(x+\phi_0)]_{a}^{b}-\int_{a}^{b}f'(x)cos(x+\phi_0)dx-[cos(x+\phi_0)f(x)]_{a}^{b}+\int_{a}^{b}cos(x+\phi_0)f'(x)dx>0 \Leftrightarrow [f'(x)sin(x+\phi_0)]_{a}^{b}-\int_{a}^{b}f'(x)cos(x+\phi_0)dx-[cos(x+\phi_0)f(x)]_{a}^{b}+\int_{a}^{b}cos(x+\phi_0)f'(x)dx>0](/forum/ext/geomar/texintegr/latexrender/pictures/55966d39c775392ffe353b221742289c.png)

 ΑΤΟΠΟ
ΑΤΟΠΟ![b\notin (a,a+\pi] b\notin (a,a+\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/b8e08c16d06f77eb6ea1fed7481a1c39.png)



 τότε
τότε 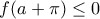 ΑΤΟΠΟ
ΑΤΟΠΟ 
Μπορείς να εξηγήσεις τα παρακάτω. Συγκεκριμένα πως πας από το πρώτο στο δεύτερο και από το δεύτερο στο τρίτο.

![\Leftrightarrow [f'(x)sin(x+\phi_0)]_{a}^{b}-\int_{a}^{b}f'(x)cos(x+\phi_0)dx-[cos(x+\phi_0)f(x)]_{a}^{b}+\int_{a}^{b}cos(x+\phi_0)f(x)dx>0 \Leftrightarrow [f'(x)sin(x+\phi_0)]_{a}^{b}-\int_{a}^{b}f'(x)cos(x+\phi_0)dx-[cos(x+\phi_0)f(x)]_{a}^{b}+\int_{a}^{b}cos(x+\phi_0)f(x)dx>0](/forum/ext/geomar/texintegr/latexrender/pictures/31e963f16ecf22c32a62006d18442976.png)

Εφαρμόζω Παραγοντική ολοκλήρωσηΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Ιαν 20, 2018 7:35 pmΜπορείς να εξηγήσεις τα παρακάτω. Συγκεκριμένα πως πας από το πρώτο στο δεύτερο και από το δεύτερο στο τρίτο.



![=[-f(x)cos(x+\phi_0)]_{a}^{b}-\int_{a}^{b}f'(x)(-cos(x+\phi_0))dx+[f'(x)sin(x+\phi_0)]_{a}^{b}-\int_{a}^{b}f'(x)(sin(x+\phi_0))'dx =[-f(x)cos(x+\phi_0)]_{a}^{b}-\int_{a}^{b}f'(x)(-cos(x+\phi_0))dx+[f'(x)sin(x+\phi_0)]_{a}^{b}-\int_{a}^{b}f'(x)(sin(x+\phi_0))'dx](/forum/ext/geomar/texintegr/latexrender/pictures/4c38f53e4b1c874742c93baacf4cad94.png)


 και
και 
 .
. και
και 
 έχουμε
έχουμε 
ΜΠΡΑΒΟmikemoke έγραψε: ↑Σάβ Ιαν 20, 2018 8:17 pmΕφαρμόζω Παραγοντική ολοκλήρωσηΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Ιαν 20, 2018 7:35 pmΜπορείς να εξηγήσεις τα παρακάτω. Συγκεκριμένα πως πας από το πρώτο στο δεύτερο και από το δεύτερο στο τρίτο.

και
άρα καταλήγουμε στο.
Στο δεύτερο κάνουμε τα ίδια αλλά με άκρα τοκαι
καταλήγουμε στο
και αφούέχουμε

 διαδοχικές ρίζες της
διαδοχικές ρίζες της  (από το 1 έτσι είναι όλες)
(από το 1 έτσι είναι όλες)




 παρουσιάζει συσσώρευση ριζών στο
παρουσιάζει συσσώρευση ριζών στο  τότε υπάρχει ακολουθία
τότε υπάρχει ακολουθία  και
και 
 και
και 

 αφού
αφού  συνεχής
συνεχής

Η λύση είναι σωστότατη και ακριβώς ίδια με την δική μου.
 παρουσιάζει συσσώρευση ριζών στο
παρουσιάζει συσσώρευση ριζών στο  τότε
τότε  με διαφορετικούς ανά δύο όρους
με διαφορετικούς ανά δύο όρους  και
και  για κάθε
για κάθε 
 μεταξύ των
μεταξύ των 


 συνεχής είναι
συνεχής είναι 



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες