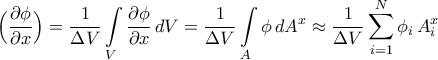
Αυτό που δεν καταλαβαίνω είναι πως είναι δυνατόν οι πρώτες δυο ισότητες να είναι αληθείς;
Θα περίμενα το παρακάτω σαν σωστή ισότητα
Ευχαριστώ εκ των προτέρων.
Συντονιστής: emouroukos
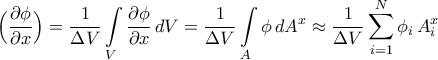
Η πρώτη ισότηταgdimitris έγραψε: ↑Πέμ Οκτ 04, 2018 2:17 amΚαλησπέρα σας, είμαι μηχανικός και προς το παρόν μελετάω την επιστήμη του CFD (Computational Fluid Dynamics), οπου ισως η πιο σοβαρή διαδικασία είναι η διακριτοποίηση μια γεωμετρίας με πλέγμα. Έτσι λοιπόν μια μέθοδος επίλυσης των διαφορικών εξισώσεων πάνω σε ένα τέτοιο πλέγμα είναι η μέθοδος των πεπερασμένων όγκων (Finite Volume Method), οπου το βιβλίο που διαβάζω δίνει την παρακάτω ισότητα
Αυτό που δεν καταλαβαίνω είναι πως είναι δυνατόν οι πρώτες δυο ισότητες να είναι αληθείς;..
 είναι εφαρμογή του θεωρήματος μέσης τιμής για ολοκληρώματα (εξ ου και το "προσέγγιση"). Για την δεύτερη ισότητα θα πρέπει να διευκρινιστεί τι είναι τα
είναι εφαρμογή του θεωρήματος μέσης τιμής για ολοκληρώματα (εξ ου και το "προσέγγιση"). Για την δεύτερη ισότητα θα πρέπει να διευκρινιστεί τι είναι τα  , αν και μοιάζει σαν εφαρμογή του θεωρήματος απόκλισης με δεδομένη κάποια συνθήκη, η οποία δεν αναφέρεται στην δημοσίευση.
, αν και μοιάζει σαν εφαρμογή του θεωρήματος απόκλισης με δεδομένη κάποια συνθήκη, η οποία δεν αναφέρεται στην δημοσίευση.
Ευχαριστώ για την απάντηση όμως υπάρχει κάτι που δεν καταλαβαίνω,grigkost έγραψε: ↑Πέμ Οκτ 04, 2018 7:47 amΗ πρώτη ισότηταgdimitris έγραψε: ↑Πέμ Οκτ 04, 2018 2:17 amΚαλησπέρα σας, είμαι μηχανικός και προς το παρόν μελετάω την επιστήμη του CFD (Computational Fluid Dynamics), οπου ισως η πιο σοβαρή διαδικασία είναι η διακριτοποίηση μια γεωμετρίας με πλέγμα. Έτσι λοιπόν μια μέθοδος επίλυσης των διαφορικών εξισώσεων πάνω σε ένα τέτοιο πλέγμα είναι η μέθοδος των πεπερασμένων όγκων (Finite Volume Method), οπου το βιβλίο που διαβάζω δίνει την παρακάτω ισότητα
Αυτό που δεν καταλαβαίνω είναι πως είναι δυνατόν οι πρώτες δυο ισότητες να είναι αληθείς;..είναι εφαρμογή του θεωρήματος μέσης τιμής για ολοκληρώματα (εξ ου και το "προσέγγιση"). Για την δεύτερη ισότητα θα πρέπει να διευκρινιστεί τι είναι τα
, αν και μοιάζει σαν εφαρμογή του θεωρήματος απόκλισης με δεδομένη κάποια συνθήκη, η οποία δεν αναφέρεται στην δημοσίευση.
1) Αυτό που αναφέρεις σαν θεώρημα μέσης τιμής έχει το σύμβολοgdimitris έγραψε: ↑Πέμ Οκτ 04, 2018 10:44 amΕυχαριστώ για την απάντηση όμως υπάρχει κάτι που δεν καταλαβαίνω,
1)Γιατί το παραπάνω είναι εφαρμογή του θεωρηματος της μεσης τιμης και δεν ειναι αυτο που παραθέτω παρακάτω
2)Επίσης, ισως κάτι δεν έχει γινει κατανοητό απο μέρους μου, η έκφρασηειναι αριθμός, σωστά;
Ηειναι αριθμός ή συνάρτηση ?
 που δεν σημαίνει τίποτα άλλο παρά αντιπαραγώγιση. Το θ.μ.τ. αφορά ολοκλήρωση σε "διάστημα" (χωρίο) και είναι αυτό που δίνει την "προσέγγιση".
που δεν σημαίνει τίποτα άλλο παρά αντιπαραγώγιση. Το θ.μ.τ. αφορά ολοκλήρωση σε "διάστημα" (χωρίο) και είναι αυτό που δίνει την "προσέγγιση". , θεωρώντας δεδομένο ότι έχει (μαθηματικώς) νόημα, πρέπει το ολοκλήρωμα να εκφράζεται σαν συνάρτηση του
, θεωρώντας δεδομένο ότι έχει (μαθηματικώς) νόημα, πρέπει το ολοκλήρωμα να εκφράζεται σαν συνάρτηση του  .
.
Η πρώτη ισότητα ισχύει σίγουρα αν ηgdimitris έγραψε: ↑Πέμ Οκτ 04, 2018 2:17 amΚαλησπέρα σας, είμαι μηχανικός και προς το παρόν μελετάω την επιστήμη του CFD (Computational Fluid Dynamics), οπου ισως η πιο σοβαρή διαδικασία είναι η διακριτοποίηση μια γεωμετρίας με πλέγμα. Έτσι λοιπόν μια μέθοδος επίλυσης των διαφορικών εξισώσεων πάνω σε ένα τέτοιο πλέγμα είναι η μέθοδος των πεπερασμένων όγκων (Finite Volume Method), οπου το βιβλίο που διαβάζω δίνει την παρακάτω ισότητα
Αυτό που δεν καταλαβαίνω είναι πως είναι δυνατόν οι πρώτες δυο ισότητες να είναι αληθείς;
Θα περίμενα το παρακάτω σαν σωστή ισότητα
Ευχαριστώ εκ των προτέρων.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Οκτ 04, 2018 1:56 pmΗ πρώτη ισότητα ισχύει σίγουρα αν ηgdimitris έγραψε: ↑Πέμ Οκτ 04, 2018 2:17 amΚαλησπέρα σας, είμαι μηχανικός και προς το παρόν μελετάω την επιστήμη του CFD (Computational Fluid Dynamics), οπου ισως η πιο σοβαρή διαδικασία είναι η διακριτοποίηση μια γεωμετρίας με πλέγμα. Έτσι λοιπόν μια μέθοδος επίλυσης των διαφορικών εξισώσεων πάνω σε ένα τέτοιο πλέγμα είναι η μέθοδος των πεπερασμένων όγκων (Finite Volume Method), οπου το βιβλίο που διαβάζω δίνει την παρακάτω ισότητα
Αυτό που δεν καταλαβαίνω είναι πως είναι δυνατόν οι πρώτες δυο ισότητες να είναι αληθείς;
Θα περίμενα το παρακάτω σαν σωστή ισότητα
Ευχαριστώ εκ των προτέρων.
είναι αρμονική συνάρτηση.
Για τις άλλες δεν έχω γνώμη γιατί υπάρχουν σύμβολα που δεν γνωρίζω τι είναι.
Απλά να σημειώσω ότι οι μηχανικοί χρησιμοποιούν συμβολισμούς διαφορετικούς από τους μαθηματικούς.
 υπολογιστικά.
υπολογιστικά.  και όγκου
και όγκου 


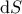 είναι το προς τα έξω κατευθυνόμενο διάνυσμα επιφανείας. Σε περίπτωση που το πεπερασμένο στοιχείο όγκου μας έχει διακριτές "έδρες" (faces) η παραπάνω σχέση γράφεται
είναι το προς τα έξω κατευθυνόμενο διάνυσμα επιφανείας. Σε περίπτωση που το πεπερασμένο στοιχείο όγκου μας έχει διακριτές "έδρες" (faces) η παραπάνω σχέση γράφεται
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες