R BORIS έγραψε: ↑Πέμ Μαρ 05, 2020 7:26 pm
πως σκέφτηκα

Θετω

Tότε
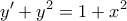
Riccati με προφανή λυση

Θετω
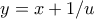
Tότε

ή

ή

ή

άρα

kαι
**** ***
***
μαλλον καποιο λάθος υπαρχει αλλά δεν το βλεπω
Λάθος υπάρχει στη τελευταία σχέση.(την έχω βάλει σε
*)
Αν θέσουμε

τότε παίρνουμε

Δεν έχουμε την γενική λύση και ο λόγος είναι απλός.
Εχουμε υποθέσει ότι

.
Πέρα από την πλάκα(την βρήκα με το μάτι) την

την βρήκα με πολύ κόπο και πολύ τύχη.
Αφού έκανα αποτυχημένες προσπάθειες με αλλαγή μεταβλητής
πήγα να βρω την λύση με δυναμοσειρά και δοκιμάζοντας την βρήκα.
Τώρα που το βλέπω μπορεί να προκύψει θέτοντας

.
Από την εμπειρία μου συνήθως στην επίλυση διαφορικών εξισώσεων
που δεν λύνονται με κάποια μέθοδο τα καταφέρνουν καλά οι Φυσικοί και οι Μηχανικοί.
 αν
αν 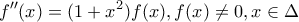






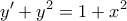 Riccati με προφανή λυση
Riccati με προφανή λυση 
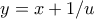
 ή
ή  ή
ή ή
ή 




 .
.
 .
.