 και για
και για  , ισχύει :
, ισχύει : , ενώ δεν ισχύει για
, ενώ δεν ισχύει για  ( δείξτε το ! ) .
( δείξτε το ! ) .Μπορούμε άραγε να βρούμε το μέγιστο άνω φράγμα για τον
 , ώστε να είναι :
, ώστε να είναι :  ;
;Σημείωση : Στο σχήμα φαίνεται ότι για
 ισχύει , αντίθετα δεν ισχύει για
ισχύει , αντίθετα δεν ισχύει για  ...
...Συντονιστής: emouroukos
 και για
και για  , ισχύει :
, ισχύει : , ενώ δεν ισχύει για
, ενώ δεν ισχύει για  ( δείξτε το ! ) .
( δείξτε το ! ) . , ώστε να είναι :
, ώστε να είναι :  ;
; ισχύει , αντίθετα δεν ισχύει για
ισχύει , αντίθετα δεν ισχύει για  ...
...Δεν ισχύει για
 διότι για
διότι για  έχουμε
έχουμε  .
. παρατηρούμε ότι για ανισότητα της μορφής
παρατηρούμε ότι για ανισότητα της μορφής  σίγουρα ισχύει στο διάστημα
σίγουρα ισχύει στο διάστημα  διότι
διότι  . Άρα προς έλεγχο είναι τα
. Άρα προς έλεγχο είναι τα  . Σε αυτή την περίπτωση έχουμε ισοδύναμα
. Σε αυτή την περίπτωση έχουμε ισοδύναμα  που διαιρώντας με το (θετικό)
που διαιρώντας με το (θετικό) 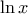 δίνει
δίνει  . Δηλαδή το βέλτιστο
. Δηλαδή το βέλτιστο  είναι η ελάχιστη τιμή, αν υπάρχει, της
είναι η ελάχιστη τιμή, αν υπάρχει, της  στο
στο ![[1, \infty ] [1, \infty ]](/forum/ext/geomar/texintegr/latexrender/pictures/f29ebb2c6344df404896fc4202fad3fa.png) . Αυτή σίγουρα υπάρχει γιατί τα όριά της στο
. Αυτή σίγουρα υπάρχει γιατί τα όριά της στο  και
και  είναι (άμεσο)
είναι (άμεσο)  .
. λαμβάνεται για
λαμβάνεται για  και η τιμή του είναι
και η τιμή του είναι  . To τελευταίο επιβεβαιώνει (όσο πιστεύουμε τον από μηχανής θεό) τους ισχυρισμούς του Θανάση ότι
. To τελευταίο επιβεβαιώνει (όσο πιστεύουμε τον από μηχανής θεό) τους ισχυρισμούς του Θανάση ότι  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες