 και η μέγιστη τιμή του
και η μέγιστη τιμή του 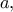 ώστε να ισχύει
ώστε να ισχύει 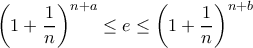
για κάθε θετικό ακέραιο
 .
.Συντονιστής: emouroukos
 και η μέγιστη τιμή του
και η μέγιστη τιμή του 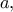 ώστε να ισχύει
ώστε να ισχύει 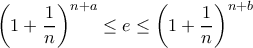
 .
.Επειδή θα μας χρειαστεί παρακάτω ας δείξουμε πρώτα
 είναι φθίνουσα στο
είναι φθίνουσα στο ![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) .
.  . Θα δείξουμε ότι είναι
. Θα δείξουμε ότι είναι  , ισοδύναμα
, ισοδύναμα  . Θέτουμε
. Θέτουμε  οπότε
οπότε  και
και  . H αποδεικτέα γίνεται
. H αποδεικτέα γίνεται 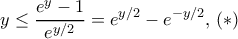 .
. 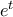 ως δυναμοσειρά, δεξί μέλος έχει ανάπτυγμα μόνο περιττές δυνάμεις του
ως δυναμοσειρά, δεξί μέλος έχει ανάπτυγμα μόνο περιττές δυνάμεις του  και όλους τους συντελεστές θετικούς. Συγκεκριμένα
και όλους τους συντελεστές θετικούς. Συγκεκριμένα 
 . Τελειώσαμε.
. Τελειώσαμε.  . Βάζοντας
. Βάζοντας  η παράσταση στη μέση γίνεται
η παράσταση στη μέση γίνεται  . Από το Λήμμα είναι φθίνουσα, δηλαδή όσο πιο μικρό το
. Από το Λήμμα είναι φθίνουσα, δηλαδή όσο πιο μικρό το  τόσο πιο μεγάλη η τιμή του
τόσο πιο μεγάλη η τιμή του  . Ειδικά η μικρότερη τιμή του προκύπτει από
. Ειδικά η μικρότερη τιμή του προκύπτει από  και η μεγαλύτερη προκύπτει οριακά (ως αύξουσα ακολουθία) από το όριό της στο
και η μεγαλύτερη προκύπτει οριακά (ως αύξουσα ακολουθία) από το όριό της στο  .
. δίνει
δίνει  . Επίσης
. Επίσης 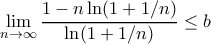 . Με διπλό l' Hospital μέσω του
. Με διπλό l' Hospital μέσω του  (απλή άσκηση αλλά και άλλος τρόπος είναι μέσω
(απλή άσκηση αλλά και άλλος τρόπος είναι μέσω  συμπεραίνουμε
συμπεραίνουμε 
 είναι βέλτιστες γιατί "πιάνονται".
είναι βέλτιστες γιατί "πιάνονται".Το θέμα τουλάχιστον σε εμένα ήταν γνωστό.
 η ακολουθία
η ακολουθία 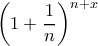 είναι μονότονη
είναι μονότονη  που δεν είναι μονότονη να αποδειχθεί ότι είναι τελικά μονότονη.
που δεν είναι μονότονη να αποδειχθεί ότι είναι τελικά μονότονη. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες