Μονοτονία παραγώγου

#1

Έστω παραγωγίσιμη συνάρτηση $f:[a,b]\rightarrow \mathbb{R}$ . Να αποδειχθεί ότι αν η

είναι γνησίως μονότονη στο (a,b)

είναι και στο [a,b]

.

#2

Καλησπέρα!

Θα υποθέσω πως η f '

είναι γνησίως αύξουσα στο $\left ( a,b \right )$ δηλαδή είναι γνησίως κυρτή στο $\left [ a ,b\right ]$ ( μιας και είναι συνεχής στο $\left [ a,b \right ]$ ).

Ας υποθέσουμε πως υπάρχει $x_{0}\in (a,b)$ τέτοιο ώστε να ισχύει $f'(a)\ge f'(x_{0})$ (1)

.

Λόγω της κυρτότητας της

η γραφική παράσταση αυτής θα είναι πάνω από την εφαπτομένη στο σημείο A(a,f(a))

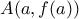εκτός από το σημείο επαφής δηλαδή θα ισχύει

$f(x)\ge f'(a)(x-a)+f(a)$ .

Λόγω της (1)

και του ότι $x-a \ge 0$ θα έχουμε ότι:

$f(x)\ge f'(x_{0})(x-a)+f(a)$ .

Για $x=x_{0}$ και δεδομένου ότι $x_{0}>a$ προκύπτει: $\frac{f(x_{0})-f(a))}{x_{0}-a} \ge f'(x_{0})$ ή (εφαρμόζοντας το Θ.Μ.Τ στο $[a,x_{0}]$ )

$f'(\xi )\ge f'(x_{0})$ για $a<\xi<x_{0}$ . Αυτό όμως είναι άτοπο αφού η

είναι γνησίως αύξουσα στο $\left ( a,b \right )$ .

Επομένως $f'(a)<f'(x), \forall x \in \left ( a,b \right )$

Κάπως παρόμοια είναι και η απόδειξη για το άλλο άκρο, το

.

Ας υποθέσουμε πως υπάρχει $x_{0}\in (a,b)$ τέτοιο ώστε να ισχύει $f'(b)\le f'(x_{0})$ (2)

.

Λόγω της κυρτότητας της

η γραφική παράσταση αυτής θα είναι πάνω από την εφαπτομένη στο σημείο B(b,f(b))

εκτός από το σημείο επαφής δηλαδή θα ισχύει

$f(x)\ge f'(b)(x-b)+f(b)$ .

Λόγω της (2)

και του ότι $x-b \le 0$ θα έχουμε ότι:

$f(x)\ge f'(x_{0})(x-b)+f(b)$ .

Για $x=x_{0}$ και δεδομένου ότι $x_{0}<b$ προκύπτει: $\frac{f(x_{0})-f(b))}{x_{0}-b} \le f'(x_{0})$ ή (εφαρμόζοντας το Θ.Μ.Τ στο $[x_{0},b]$ )

$f'(\xi )\le f'(x_{0})$ για $x_{0}<\xi< b$ . Αυτό όμως είναι άτοπο αφού η

είναι γνησίως αύξουσα στο $\left ( a,b \right )$ .

Επομένως $f'(x)<f'(b), \forall x \in \left ( a,b \right )$

Άρα η

είναι γnησιώς αύξουσα στο $\left [ a,b \right ]$ .

Με όμοιο τρόπο μπορούμε να εργαστούμε όταν η

είναι κοίλη.

#3

chris_gatos έγραψε: ↑
Σάβ Ιαν 16, 2021 7:23 pm
Καλησπέρα!

Θα υποθέσω πως η είναι γνησίως αύξουσα στο $\left ( a,b \right )$ δηλαδή είναι γνησίως κυρτή στο $\left [ a ,b\right ]$ ( μιας και είναι συνεχής στο $\left [ a,b \right ]$ ).

Ας υποθέσουμε πως υπάρχει $x_{0}\in (a,b)$ τέτοιο ώστε να ισχύει $f'(a)\ge f'(x_{0})$ .

...

Γειά σας
Χρήστο ευχαριστώ γα την απάντηση. Έχει το πλεονέκτημα ότι είναι διδάξιμη σε τάξη.
Η απόδειξη που είχα υπ' όψιν στηρίζεται στο θεώρημα του Darboux (η παράγωγος σε διάστημα έχει την ιδιότητα της ενδιάμεσης τιμής): Αν υποτεθεί ότι υπάρχει $x_{0}\in (a,b)$ τέτοιο ώστε να ισχύει $f'(a)\ge f'(x_{0})$ τότε επιλέγοντας

μεταξύ των

,

θα είναι $f'(t)<f'(x_{0}) \leq f'(a)$ και για τις τιμές f'(a)>f'(t)

της

θα υπάρχει

στο

ώστε

. Το τελευταίο έρχεται σε αντίθεση με την μονοτονία της παραγώγου στο (a,b)

.

Μονοτονία παραγώγου

Μονοτονία παραγώγου

Re: Μονοτονία παραγώγου

Re: Μονοτονία παραγώγου

Μέλη σε σύνδεση