![f:[0,1]\to\mathbb R f:[0,1]\to\mathbb R](/forum/ext/geomar/texintegr/latexrender/pictures/2b80fa95661cd96d5ba60c3aa700e464.png) συνεχής. Δείξατε ὅτι
συνεχής. Δείξατε ὅτι
Συντονιστής: emouroukos
Μιας και κάνω τον κόπο θα δείξω το ισχυρότερο
![f:[0,1]\to\mathbb R f:[0,1]\to\mathbb R](/forum/ext/geomar/texintegr/latexrender/pictures/2b80fa95661cd96d5ba60c3aa700e464.png) Lebesgue ολοκληρώσιμη συνάρτηση συνεχής στο
Lebesgue ολοκληρώσιμη συνάρτηση συνεχής στο  .
.


 (1)
(1) (2)
(2)
 υπάρχει
υπάρχει  ώστε
ώστε
 (4)
(4)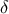 φράσσεται απόλυτα από μια σταθερά.
φράσσεται απόλυτα από μια σταθερά.


 και λαμβάνοντας υπ οψιν την τελευταία και την (2)
και λαμβάνοντας υπ οψιν την τελευταία και την (2)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες