Πάνω στη γραφική παράσταση της συνάρτησης :
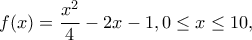
κινούνται τα σημεία
 . Βρείτε το μέγιστο μήκος του τμήματος
. Βρείτε το μέγιστο μήκος του τμήματος  .
.Συντονιστής: emouroukos
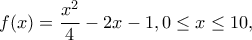
 . Βρείτε το μέγιστο μήκος του τμήματος
. Βρείτε το μέγιστο μήκος του τμήματος  .
.Αυτό θα πρέπει να αιτιολογηθεί.orestisgotsis έγραψε: ↑Πέμ Ιαν 19, 2023 4:33 amΗ σκέψη μου είναι η εξής: Να αφήσω το T να πάρει την πιο ψηλή τιμή και το S να
 ισχύουν:
ισχύουν: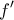 θετική στο
θετική στο ![\displaystyle{(4,10]} \displaystyle{(4,10]}](/forum/ext/geomar/texintegr/latexrender/pictures/e4cf89d4135e17f39d97d9d3cffae8a8.png) και αρνητική στο
και αρνητική στο 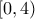 και συνεπώς η
και συνεπώς η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\displaystyle{[0,4]} \displaystyle{[0,4]}](/forum/ext/geomar/texintegr/latexrender/pictures/c61be56947799f444c9605b715f7960c.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο ![\displaystyle{[4,10]} \displaystyle{[4,10]}](/forum/ext/geomar/texintegr/latexrender/pictures/3df31a6d51d72fdc925b720e746a914b.png)
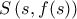 και
και 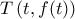 με
με  , θα δείξουμε ότι για τυχαίο
, θα δείξουμε ότι για τυχαίο  είναι
είναι 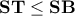 για κάθε
για κάθε 
![\displaystyle{\left(ST\right)^2=(t-s)^2+\left(f(t)-f(s)\right)^2=g(t), \ \ t\in (0,10]} \displaystyle{\left(ST\right)^2=(t-s)^2+\left(f(t)-f(s)\right)^2=g(t), \ \ t\in (0,10]}](/forum/ext/geomar/texintegr/latexrender/pictures/35319958f816e6e494fe37864fa2ca18.png)
![\displaystyle{g^{\prime}(t)=2(t-s)+2\left(f(t)-f(s)\right)\cdot f^{\prime}(t)>0 \ \ \forall t \in (0,10]} \displaystyle{g^{\prime}(t)=2(t-s)+2\left(f(t)-f(s)\right)\cdot f^{\prime}(t)>0 \ \ \forall t \in (0,10]}](/forum/ext/geomar/texintegr/latexrender/pictures/3fca7d6f7f3f65b1e11f1de629fd70a8.png) αφού
αφού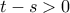 και
και ![\displaystyle{t\in (0,4]} \displaystyle{t\in (0,4]}](/forum/ext/geomar/texintegr/latexrender/pictures/651431104781adb57b2056dea44dff97.png) :
: 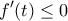 και
και 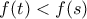
![\displaystyle{t\in [4,10]} \displaystyle{t\in [4,10]}](/forum/ext/geomar/texintegr/latexrender/pictures/334046bb6af44c3b895d50fc6f2ab14b.png) :
: 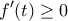 και
και 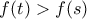
 είναι γνησίως αύξουσα οπότε:
είναι γνησίως αύξουσα οπότε: 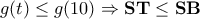


Ξαναβλέποντάς το παρατηρώ ότι θα πρέπει να θεωρήσουμε και την "αντίθετη" περίπτωση, δηλαδή να είναι μεταβλητό τοabgd έγραψε: ↑Πέμ Ιαν 19, 2023 12:49 pmΑυτό θα πρέπει να αιτιολογηθεί.orestisgotsis έγραψε: ↑Πέμ Ιαν 19, 2023 4:33 amΗ σκέψη μου είναι η εξής: Να αφήσω το T να πάρει την πιο ψηλή τιμή και το S να
Για τη συνάρτησηισχύουν:
θετική στο
και αρνητική στο
και συνεπώς η
είναι γνησίως φθίνουσα στο
και γνησίως αύξουσα στο
Ανκαι
με
, θα δείξουμε ότι για τυχαίο
είναι
για κάθε
Είναι
αφού
και
- για κάθε
:
και
Έτσι, η συνάρτηση
- για κάθε
:
και
είναι γνησίως αύξουσα οπότε:
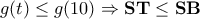
 και σταθερό το
και σταθερό το  .
.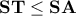 .
.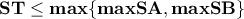 .
. 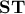 θα είναι ίση με τη μεγαλύτερη από τις τιμές που μπορούν να πάρουν τα
θα είναι ίση με τη μεγαλύτερη από τις τιμές που μπορούν να πάρουν τα 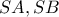 .
.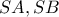 θεωρώντας βέβαια το
θεωρώντας βέβαια το 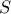 μεταβλητό.
μεταβλητό.

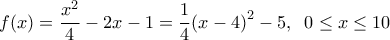 , οπότε το πρόβλημα μπορεί να διατυπωθεί:
, οπότε το πρόβλημα μπορεί να διατυπωθεί: 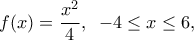 κινούνται τα σημεία
κινούνται τα σημεία  . Βρείτε το μέγιστο μήκος του τμήματος
. Βρείτε το μέγιστο μήκος του τμήματος  .
.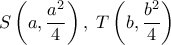 σημεία της
σημεία της 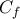 , με
, με 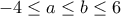 .
.![\displaystyle ST = \sqrt {{{\left( {b - a} \right)}^2} + {{\left( {\frac{{{b^2} - {a^2}}}{4}} \right)}^2}} \;\;\;a,b \in \left[ { - 4,6} \right] \displaystyle ST = \sqrt {{{\left( {b - a} \right)}^2} + {{\left( {\frac{{{b^2} - {a^2}}}{4}} \right)}^2}} \;\;\;a,b \in \left[ { - 4,6} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/6b8d85bec1525a4b3d2153773120b9fc.png)
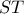 έχει μέγιστο όταν λάβει τη μέγιστη τιμή της η παράσταση
έχει μέγιστο όταν λάβει τη μέγιστη τιμή της η παράσταση ![\displaystyle {\left( {b - a} \right)^2} + {\left( {\frac{{{b^2} - {a^2}}}{4}} \right)^2}\;\;\;a,b \in \left[ { - 4,6} \right] \displaystyle {\left( {b - a} \right)^2} + {\left( {\frac{{{b^2} - {a^2}}}{4}} \right)^2}\;\;\;a,b \in \left[ { - 4,6} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/81046fff772079ae79470a1fac603f21.png)
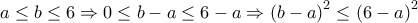
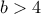 , τότε
, τότε 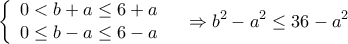
![\displaystyle {\left( {b - a} \right)^2} + {\left( {\frac{{{b^2} - {a^2}}}{4}} \right)^2}\; \le {\left( {6 - a} \right)^2} + {\left( {\frac{{36 - {a^2}}}{4}} \right)^2}\;\;a \in \left[ { - 4,6} \right] \displaystyle {\left( {b - a} \right)^2} + {\left( {\frac{{{b^2} - {a^2}}}{4}} \right)^2}\; \le {\left( {6 - a} \right)^2} + {\left( {\frac{{36 - {a^2}}}{4}} \right)^2}\;\;a \in \left[ { - 4,6} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/6a1c23c6e9d6d646d0dc90ee2deb09ef.png)
![\displaystyle h\left( a \right) = {\left( {6 - a} \right)^2} + \frac{{{{\left( {36 - {a^2}} \right)}^2}}}{{16}},\;\;a \in \left[ { - 4,6} \right] \displaystyle h\left( a \right) = {\left( {6 - a} \right)^2} + \frac{{{{\left( {36 - {a^2}} \right)}^2}}}{{16}},\;\;a \in \left[ { - 4,6} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/11ebf4bf4e561563d2db5b34a8a65b3d.png)
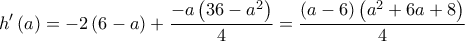
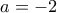 με τιμή
με τιμή 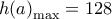 . Τότε
. Τότε 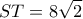
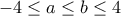 , τότε
, τότε 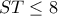 , αφού η παραβολή
, αφού η παραβολή ![\displaystyle y = \frac{{{x^2}}}{4},\;\;x \in \left[ { - 4,4} \right] \displaystyle y = \frac{{{x^2}}}{4},\;\;x \in \left[ { - 4,4} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a657eb6531da6e913b3c5050dedd2e09.png)
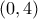 και ακτίνα
και ακτίνα 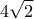 .
.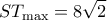 , όταν
, όταν 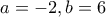 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες