 το σύνολο των συνεχών συναρτήσεων
το σύνολο των συνεχών συναρτήσεων ![\displaystyle f:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-1,1] \displaystyle f:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ea72d5caf58979184c0297eee0f99361.png)
που είναι παραγωγίσιμες στο
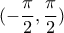
Να υπολογισθεί το
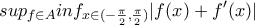
Συντονιστής: emouroukos
 το σύνολο των συνεχών συναρτήσεων
το σύνολο των συνεχών συναρτήσεων ![\displaystyle f:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-1,1] \displaystyle f:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ea72d5caf58979184c0297eee0f99361.png)
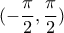
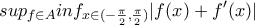
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Σεπ 10, 2023 9:42 pmΕστωτο σύνολο των συνεχών συναρτήσεων
που είναι παραγωγίσιμες στο
Να υπολογισθεί το
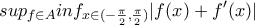
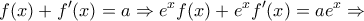 ,
,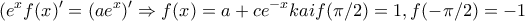 οπότε
οπότε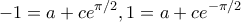
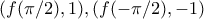
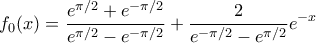 αλλά
αλλά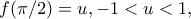 τοτε οι διαφορες f καλυπτουν ολα τα σημεια του χωριου που βρίσκεται κατω απο την
τοτε οι διαφορες f καλυπτουν ολα τα σημεια του χωριου που βρίσκεται κατω απο την 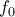 kαι είναι ταυτόχρονα στο εσωτερικό του ορθογωνιου
kαι είναι ταυτόχρονα στο εσωτερικό του ορθογωνιου 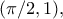 (-\pi/2,1),
(-\pi/2,1),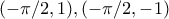
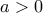 οποτε
οποτε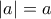 αναλογα Και αν
αναλογα Και αν 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες