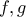 είναι συνεχείς στο
είναι συνεχείς στο ![[a , b] [a , b]](/forum/ext/geomar/texintegr/latexrender/pictures/999c78069151678c7f73cb224da7cb6a.png) και ισχύουν :
και ισχύουν : 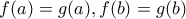
και :
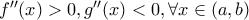 . Δείξτε ότι :
. Δείξτε ότι : 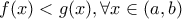 .
. Μπορούμε να χρησιμοποιούμε το παραπάνω λήμμα χωρίς απόδειξη ;
Συντονιστής: emouroukos
Μη αναγνωσμένη δημοσίευση από KARKAR » Πέμ Απρ 11, 2024 1:24 pm
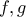 είναι συνεχείς στο
είναι συνεχείς στο ![[a , b] [a , b]](/forum/ext/geomar/texintegr/latexrender/pictures/999c78069151678c7f73cb224da7cb6a.png) και ισχύουν :
και ισχύουν : 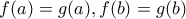
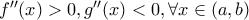 . Δείξτε ότι :
. Δείξτε ότι : 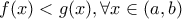 .
. Μη αναγνωσμένη δημοσίευση από matha » Πέμ Απρ 11, 2024 6:14 pm
 είναι κυρτή στο
είναι κυρτή στο ![\displaystyle{[a,b]} \displaystyle{[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/14f53999651f504e8f7c5c1b74530f3e.png) τότε το μέγιστό της είναι το
τότε το μέγιστό της είναι το 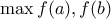 , το οποίο, αν και προφανές διαισθητικά, θέλει απόδειξη.
, το οποίο, αν και προφανές διαισθητικά, θέλει απόδειξη.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off