 , ενός ημικυκλίου , θεωρούμε σημείο
, ενός ημικυκλίου , θεωρούμε σημείο  , ώστε :
, ώστε : 
και στην ακτίνα
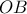 σημείο
σημείο  , ώστε
, ώστε  . Μία τέμνουσα
. Μία τέμνουσα  του τόξου , τέμνει την κάθετη
του τόξου , τέμνει την κάθετητης διαμέτρου στο
 , στο σημείο
, στο σημείο  . Για ποια θέση της τέμνουσας ελαχιστοποιείται ο λόγος :
. Για ποια θέση της τέμνουσας ελαχιστοποιείται ο λόγος :  ;
;Συντονιστής: gbaloglou
 , ενός ημικυκλίου , θεωρούμε σημείο
, ενός ημικυκλίου , θεωρούμε σημείο  , ώστε :
, ώστε : 
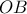 σημείο
σημείο  , ώστε
, ώστε  . Μία τέμνουσα
. Μία τέμνουσα  του τόξου , τέμνει την κάθετη
του τόξου , τέμνει την κάθετη , στο σημείο
, στο σημείο  . Για ποια θέση της τέμνουσας ελαχιστοποιείται ο λόγος :
. Για ποια θέση της τέμνουσας ελαχιστοποιείται ο λόγος :  ;
;KARKAR έγραψε: ↑Κυρ Μάιος 09, 2021 8:15 pmΑπίθανο ελάχιστο λόγου.pngΣτην προέκταση της διαμέτρου, ενός ημικυκλίου , θεωρούμε σημείο
, ώστε :
και στην ακτίνασημείο
, ώστε
. Μία τέμνουσα
του τόξου , τέμνει την κάθετη
της διαμέτρου στο, στο σημείο
. Για ποια θέση της τέμνουσας ελαχιστοποιείται ο λόγος :
;

 Θέτω
Θέτω  άρα
άρα 
 Εφαρμόζω νόμο συνημιτόνου στα τρίγωνα
Εφαρμόζω νόμο συνημιτόνου στα τρίγωνα  και έχω:
και έχω: και από την
και από την  οι
οι 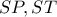 είναι ρίζες της εξίσωσης:
είναι ρίζες της εξίσωσης: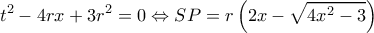 και
και 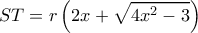


 όταν
όταν 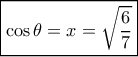
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες