 και ευθεία
και ευθεία  . Οι αποστάσεις των κορυφών
. Οι αποστάσεις των κορυφών  από την ευθεία
από την ευθεία  είναι
είναι  αντίστοιχα.
αντίστοιχα.Να αποδείξετε ότι

όπου
 το εμβαδόν του τριγώνου.
το εμβαδόν του τριγώνου.Πότε ισχύει η ισότητα;
Συντονιστής: gbaloglou
 και ευθεία
και ευθεία  . Οι αποστάσεις των κορυφών
. Οι αποστάσεις των κορυφών  από την ευθεία
από την ευθεία  είναι
είναι  αντίστοιχα.
αντίστοιχα.
 το εμβαδόν του τριγώνου.
το εμβαδόν του τριγώνου. , ώστε η ευθεία
, ώστε η ευθεία  να ταυτίζεται με τον άξονα των
να ταυτίζεται με τον άξονα των  και η κάθετη ευθεία από το
και η κάθετη ευθεία από το 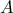 προς την
προς την  να ταυτίζεται με τον άξονα των
να ταυτίζεται με τον άξονα των  . Τότε, έχουμε ότι
. Τότε, έχουμε ότι  ,
,  και
και  όπου
όπου  Άρα, θα είναι:
Άρα, θα είναι:




 έχει εξίσωση
έχει εξίσωση  όπου
όπου  με
με  Τότε, θα είναι:
Τότε, θα είναι:


![\displaystyle {x^2}\tan A + {y^2}\tan B + {z^2}\tan C = \frac{1}{{{r^2} + {s^2}}}\left[ {{{\left( {sa + t} \right)}^2}\frac{{a\left( {b + c} \right)}}{{{a^2} - bc}} + {{\left( { - rb + t} \right)}^2}\frac{a}{b} + {{\left( {rc + t} \right)}^2}\frac{a}{c}} \right] = \displaystyle {x^2}\tan A + {y^2}\tan B + {z^2}\tan C = \frac{1}{{{r^2} + {s^2}}}\left[ {{{\left( {sa + t} \right)}^2}\frac{{a\left( {b + c} \right)}}{{{a^2} - bc}} + {{\left( { - rb + t} \right)}^2}\frac{a}{b} + {{\left( {rc + t} \right)}^2}\frac{a}{c}} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/09f12359218812ce86a3e3ff4b02368d.png)
![\displaystyle = \frac{a}{{{r^2} + {s^2}}}\left[ {{{\left( {sa + t} \right)}^2}\frac{{b + c}}{{{a^2} - bc}} + \frac{1}{{bc}}\left( {c{{\left( { - rb + t} \right)}^2} + b{{\left( {rc + t} \right)}^2}} \right)} \right] = \displaystyle = \frac{a}{{{r^2} + {s^2}}}\left[ {{{\left( {sa + t} \right)}^2}\frac{{b + c}}{{{a^2} - bc}} + \frac{1}{{bc}}\left( {c{{\left( { - rb + t} \right)}^2} + b{{\left( {rc + t} \right)}^2}} \right)} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/6040b64c6c1f59e60f59b43513422d74.png)
![\displaystyle = \frac{a}{{{r^2} + {s^2}}}\left[ {{{\left( {sa + t} \right)}^2}\frac{{b + c}}{{{a^2} - bc}} + \frac{1}{{bc}}\left( {{r^2}{b^2}c - 2rtbc + c{t^2} + {r^2}b{c^2} + 2rtbc + b{t^2}} \right)} \right] = \displaystyle = \frac{a}{{{r^2} + {s^2}}}\left[ {{{\left( {sa + t} \right)}^2}\frac{{b + c}}{{{a^2} - bc}} + \frac{1}{{bc}}\left( {{r^2}{b^2}c - 2rtbc + c{t^2} + {r^2}b{c^2} + 2rtbc + b{t^2}} \right)} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/419ea5ea359a8819f54aa3719d342899.png)
![\displaystyle = \frac{a}{{{r^2} + {s^2}}}\left[ {{{\left( {sa + t} \right)}^2}\frac{{b + c}}{{{a^2} - bc}} + \frac{{b + c}}{{bc}}\left( {{r^2}bc + {t^2}} \right)} \right] = \displaystyle = \frac{a}{{{r^2} + {s^2}}}\left[ {{{\left( {sa + t} \right)}^2}\frac{{b + c}}{{{a^2} - bc}} + \frac{{b + c}}{{bc}}\left( {{r^2}bc + {t^2}} \right)} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/407288a61d2356ab4867fd5c14519348.png)
![\displaystyle = \frac{{a\left( {b + c} \right)}}{{{r^2} + {s^2}}}\left[ {\frac{{{{\left( {sa + t} \right)}^2}}}{{{a^2} - bc}} + \frac{{{r^2}bc + {t^2}}}{{bc}}} \right] = \displaystyle = \frac{{a\left( {b + c} \right)}}{{{r^2} + {s^2}}}\left[ {\frac{{{{\left( {sa + t} \right)}^2}}}{{{a^2} - bc}} + \frac{{{r^2}bc + {t^2}}}{{bc}}} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/b3f0f3748d3a3d68f5599805a1adadeb.png)




 δηλαδή αν και μόνο αν το σημείο
δηλαδή αν και μόνο αν το σημείο  ανήκει στην ευθεία
ανήκει στην ευθεία  . Αλλά είναι
. Αλλά είναι
 και άρα το σημείο
και άρα το σημείο  είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  Συνεπώς, η ισότητα ισχύει αν και μόνο αν η ευθεία
Συνεπώς, η ισότητα ισχύει αν και μόνο αν η ευθεία  διέρχεται από το ορθόκεντρο
διέρχεται από το ορθόκεντρο  του τριγώνου
του τριγώνου 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες