 είναι το μέσο της ακτίνας
είναι το μέσο της ακτίνας  κύκλου
κύκλου  και το
και το  σημείο του .
σημείο του .Η ευθεία
 τέμνει την εφαπτομένη του κύκλου στο
τέμνει την εφαπτομένη του κύκλου στο  , σε σημείο
, σε σημείο  ,
,ενώ η εφαπτομένη στο
 την τέμνει στο
την τέμνει στο  . Ψάχνουμε για το
. Ψάχνουμε για το  ...
...Συντονιστής: gbaloglou
 είναι το μέσο της ακτίνας
είναι το μέσο της ακτίνας  κύκλου
κύκλου  και το
και το  σημείο του .
σημείο του . τέμνει την εφαπτομένη του κύκλου στο
τέμνει την εφαπτομένη του κύκλου στο  , σε σημείο
, σε σημείο  ,
, την τέμνει στο
την τέμνει στο  . Ψάχνουμε για το
. Ψάχνουμε για το  ...
... και
και  , θεωρήσω δε
, θεωρήσω δε  με :
με : βρίσκω με τη βοήθεια λογισμικού
βρίσκω με τη βοήθεια λογισμικού  και
και  .
. και
και  , θεωρήσω δε
, θεωρήσω δε  με :
με : βρίσκω με τη βοήθεια λογισμικού
βρίσκω με τη βοήθεια λογισμικού  και
και  .
. θα επαληθεύει τον κύκλο
θα επαληθεύει τον κύκλο  , οπότε:
, οπότε: 
 .
. είναι
είναι  που για
που για 
 . Η εξίσωση της
. Η εξίσωση της  . Πάλι για
. Πάλι για  έχω
έχω  οπότε
οπότε 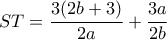 κι αφού το ύψος του
κι αφού το ύψος του 
 το εμβαδόν του είναι
το εμβαδόν του είναι  που λόγω της (1)
που λόγω της (1) 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης