Είναι τα ορθογώνια τρίγωνα ίσα;
Συντονιστής: gbaloglou
Είναι τα ορθογώνια τρίγωνα ίσα;
Δύο ορθογώνια τρίγωνα τα οποία έχουν ίσες μια προς μια τις διχοτόμους τους προς τις κάθετες πλευρές τους , είναι ίσα;
Λέξεις Κλειδιά:
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
Και άλλη μία
Δύο ορθογώνια τρίγωνα τα οποία έχουν ίσες μια προς μια τις διαμέσους τους προς τις κάθετες πλευρές τους , είναι ίσα;
Δύο ορθογώνια τρίγωνα τα οποία έχουν ίσες μια προς μια τις διαμέσους τους προς τις κάθετες πλευρές τους , είναι ίσα;
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
Αρκεί να δείξω ότι ένα ορθογώνιο τρίγωνο
 κατασκευάζεται αν είναι γνωστά τα μήκη των διαμέσων του
κατασκευάζεται αν είναι γνωστά τα μήκη των διαμέσων του 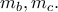 Πράγματι,
Πράγματι,  Άρα η υποτείνουσα έχει σταθερό μήκος. Προφανώς λοιπόν, το
Άρα η υποτείνουσα έχει σταθερό μήκος. Προφανώς λοιπόν, το  ορίζεται μονοσήμαντα.
ορίζεται μονοσήμαντα.- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
Καλησπέρα σε όλους. Είπα: "Επειδή έμεινε αρκετές ημέρες αναπάντητο είτε πέρασε απαρατήρητο, είτε θα έχει ενδιαφέρον η ενασχόληση μ' αυτό". Τείνω προς τη δεύτερη άποψη (με την επιφύλαξη να είναι κάτι απλό, το οποίο δεν βλέπω, εγκλωβισμένος στην πρώτη σκέψη).
Επιχειρώ δύο προσεγγίσεις.
Κατασκευαστική:
Έστω
 δεδομένοι σταθεροί θετικοί αριθμοί.
δεδομένοι σταθεροί θετικοί αριθμοί.Σε ευθεία
 παίρνουμε σημείο
παίρνουμε σημείο  και κατασκευάζουμε κύκλο
και κατασκευάζουμε κύκλο  , που τέμνει την ευθεία
, που τέμνει την ευθεία  στο
στο  .
. Έστω σημείο
 στο τόξο
στο τόξο  που είναι ίσο με το
που είναι ίσο με το  του κύκλου.
του κύκλου.Φέρνουμε
 κάθετη στην
κάθετη στην  και τη διχοτόμο της
και τη διχοτόμο της  που τέμνει τη
που τέμνει τη  στο
στο  .
. Κατασκευάζουμε ημιευθεία
 ώστε η
ώστε η  να διχοτομεί τη γωνία
να διχοτομεί τη γωνία 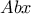 .
.Η ημιευθεία
 τέμνει την προέκταση της
τέμνει την προέκταση της  στο
στο  . Η
. Η  τέμνει την
τέμνει την  στο
στο  .
.Όπως το
 διατρέχει το τόξο
διατρέχει το τόξο  από το
από το  προς το
προς το  , τότε το
, τότε το  διατρέχει το διάστημα
διατρέχει το διάστημα  , αυξανόμενο συνεχώς, οπότε για κάποια μοναδική θέση του
, αυξανόμενο συνεχώς, οπότε για κάποια μοναδική θέση του  θα είναι ίσο με
θα είναι ίσο με  , οπότε η κατασκευή του ορθογωνίου τριγώνου
, οπότε η κατασκευή του ορθογωνίου τριγώνου  με διχοτόμους
με διχοτόμους  γίνεται με μοναδικό τρόπο.
γίνεται με μοναδικό τρόπο.ΣΧΟΛΙΟ: Γνωρίζω ότι η τελευταία παράγραφος είναι εκτός ορίων της Ευκλείδειας προσέγγισης.Με ενδιαφέρουν οι απόψεις, τα σχόλια, οι διορθώσεις ή οι συμπληρώσεις σας.
Δίνω το αρχείο Geogebra.
- Συνημμένα
-
- 11-11-2019 Γεωμετρία b.ggb
- (25.79 KiB) Μεταφορτώθηκε 10 φορές
τελευταία επεξεργασία από Γιώργος Ρίζος σε Δευ Νοέμ 11, 2019 9:35 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
2η προσέγγιση. Αλγεβρική:
Έστω δεδομένα σταθερά μήκη τμημάτων.
δεδομένα σταθερά μήκη τμημάτων.
Σε ορθή γωνία παίρνουμε τμήματα
παίρνουμε τμήματα  ..
..
Όμως είναι


 .
.
Η εξίσωση αυτή μπορεί να δειχθεί ότι έχει μοναδική λύση όταν .
.
Είναι κουραστικό. Δεν το προχωρώ, περιμένοντας πιο απλή λύση.
Έστω
 δεδομένα σταθερά μήκη τμημάτων.
δεδομένα σταθερά μήκη τμημάτων.Σε ορθή γωνία
 παίρνουμε τμήματα
παίρνουμε τμήματα  ..
..Όμως είναι


 .
.Η εξίσωση αυτή μπορεί να δειχθεί ότι έχει μοναδική λύση όταν
 .
.Είναι κουραστικό. Δεν το προχωρώ, περιμένοντας πιο απλή λύση.
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
Καλησπέρα κ. Βισβίκη και κ. Ρίζο.
Σας ευχαριστώ πολύ για τις ιδέες σας.
Τον τελευταίο καιρό πειραματίζομαι με όλες τις περιπτώσεις κριτηρίων ισότητας (ορθογωνίων) τριγώνων, συνδυάζοντας όλες τις περιπτώσεις πρωτευόντων και δευτερευόντων στοιχείων του τριγώνου. Άλλες βγήκαν εύκολα, άλλες δύσκολα και άλλες στις οποίες δεν ... φαίνεται το παραμικρό φως στο τούνελ! Σίγουρα με τον καιρό και την ανταλλαγή ιδεών, θα βρούμε όμορφες και πρωτόγνωρες λύσεις.
Να στε πάντα καλά και συνεχίζουμε!
Σας ευχαριστώ πολύ για τις ιδέες σας.
Τον τελευταίο καιρό πειραματίζομαι με όλες τις περιπτώσεις κριτηρίων ισότητας (ορθογωνίων) τριγώνων, συνδυάζοντας όλες τις περιπτώσεις πρωτευόντων και δευτερευόντων στοιχείων του τριγώνου. Άλλες βγήκαν εύκολα, άλλες δύσκολα και άλλες στις οποίες δεν ... φαίνεται το παραμικρό φως στο τούνελ! Σίγουρα με τον καιρό και την ανταλλαγή ιδεών, θα βρούμε όμορφες και πρωτόγνωρες λύσεις.
Να στε πάντα καλά και συνεχίζουμε!
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3342
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
Τοποθετούμε τα δύο ορθογώνια τρίγωνα σε σύστημα συντεταγμένων ως {
 } και {
} και { }. Οι ισότητες των δύο διαμέσων σημαίνουν ότι είναι ίσες οι αποστάσεις ανάμεσα σε
}. Οι ισότητες των δύο διαμέσων σημαίνουν ότι είναι ίσες οι αποστάσεις ανάμεσα σε  ,
,  και
και  ,
,  και ότι είναι ίσες οι αποστάσεις ανάμεσα σε
και ότι είναι ίσες οι αποστάσεις ανάμεσα σε  ,
,  , και
, και  ,
,  . Ισχύουν δηλαδή οι εξισώσεις
. Ισχύουν δηλαδή οι εξισώσεις  και
και  . Η ταυτόχρονη ισχύς των
. Η ταυτόχρονη ισχύς των  και
και  συνεπάγεται την
συνεπάγεται την  , άρα
, άρα  (και
(και  ): τα δύο ορθογώνια τρίγωνα είναι ίσα.
): τα δύο ορθογώνια τρίγωνα είναι ίσα.[Η αντίστοιχη προσέγγιση για τις διχοτόμους οδηγεί στην εξής αλγεβρική εικασία:
αν
 και
και 
τότε
 και
και  .]
.]Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
Ολοκληρώνοντας την προηγούμενη δημοσίευσή μου, θα δώσω την κατασκευή ενός ορθογωνίου τριγώνου  όταν δίνονται οι διάμεσοι
όταν δίνονται οι διάμεσοι  Εύκολα βρίσκω
Εύκολα βρίσκω  άρα το μήκος της
άρα το μήκος της  είναι σταθερό.
είναι σταθερό.
Κατασκευάζω το τρίγωνο με
με 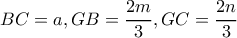 και στη συνέχεια προεκτείνω τις
και στη συνέχεια προεκτείνω τις  κατά τμήματα
κατά τμήματα  Το σημείο τομής των
Το σημείο τομής των  είναι η τρίτη κορυφή
είναι η τρίτη κορυφή  του τριγώνου.
του τριγώνου.
Εναλλακτικά, οι τρεις διάμεσοι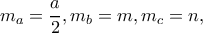 έχουν γνωστά μήκη, άρα το τρίγωνο
έχουν γνωστά μήκη, άρα το τρίγωνο  είναι μονοσήμαντα ορισμένο (κλασική κατασκευή).
είναι μονοσήμαντα ορισμένο (κλασική κατασκευή).
 όταν δίνονται οι διάμεσοι
όταν δίνονται οι διάμεσοι  Εύκολα βρίσκω
Εύκολα βρίσκω  άρα το μήκος της
άρα το μήκος της  είναι σταθερό.
είναι σταθερό.Κατασκευάζω το τρίγωνο
 με
με 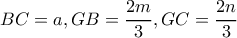 και στη συνέχεια προεκτείνω τις
και στη συνέχεια προεκτείνω τις  κατά τμήματα
κατά τμήματα  Το σημείο τομής των
Το σημείο τομής των  είναι η τρίτη κορυφή
είναι η τρίτη κορυφή  του τριγώνου.
του τριγώνου.Εναλλακτικά, οι τρεις διάμεσοι
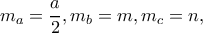 έχουν γνωστά μήκη, άρα το τρίγωνο
έχουν γνωστά μήκη, άρα το τρίγωνο  είναι μονοσήμαντα ορισμένο (κλασική κατασκευή).
είναι μονοσήμαντα ορισμένο (κλασική κατασκευή).- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3342
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
Γιώργο ούτε άλλη λύση βρέθηκε ως τώρα, ούτε κουραστικό είναι τελικά:Γιώργος Ρίζος έγραψε: ↑Δευ Νοέμ 11, 2019 9:14 pm2η προσέγγιση. Αλγεβρική:
10-11-2019 Γεωμετρία.jpg
Έστωδεδομένα σταθερά μήκη τμημάτων.
Σε ορθή γωνίαπαίρνουμε τμήματα
..
Όμως είναι


.
Η εξίσωση αυτή μπορεί να δειχθεί ότι έχει μοναδική λύση όταν.
Είναι κουραστικό. Δεν το προχωρώ, περιμένοντας πιο απλή λύση.
Χρησιμοποιώντας το ανεξαρτήτου ενδιαφέροντος λήμμα που παρέθεσα εδώ, παρατηρούμε ότι για να έχει μοναδική λύση για
 η παραπάνω
η παραπάνω  ... αρκεί να έχει μία το πολύ λύση για
... αρκεί να έχει μία το πολύ λύση για  η
η 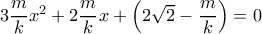 : αυτό είναι φανερό από την
: αυτό είναι φανερό από την 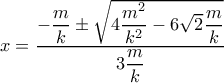 .
.Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
Έστω
 τα (άγνωστα) μήκη των πλευρών. Υποθέτω ότι η
τα (άγνωστα) μήκη των πλευρών. Υποθέτω ότι η  είναι η ορθή γωνία. Τα μήκη των διχοτόμων είναι
είναι η ορθή γωνία. Τα μήκη των διχοτόμων είναι και
και 
Παρατηρούμε ότι
 και
και 
Άρα η
 είναι αύξουσα τόσο ως προς το
είναι αύξουσα τόσο ως προς το  όσο και ως προς το
όσο και ως προς το  .
.Αν τώρα έχουμε και δεύτερο τρίγωνο με τα ίδια μήκη διχοτόμων και μήκη πλευρών
 όπου χωρίς βλάβη της γενικότητας
όπου χωρίς βλάβη της γενικότητας  , τότε:
, τότε:Αφού η
 είναι κοινή και αύξουσα ως προς
είναι κοινή και αύξουσα ως προς  πρέπει
πρέπει  . Με το ίδιο σκεπτικό, επειδή η
. Με το ίδιο σκεπτικό, επειδή η 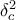 είναι κοινή και αύξουσα ως προς
είναι κοινή και αύξουσα ως προς  πρέπει
πρέπει  . Αυτό είναι άτοπο διότι
. Αυτό είναι άτοπο διότι
Άρα τα τρίγωνα πρέπει να είναι ίσα.
Re: Είναι τα ορθογώνια τρίγωνα ίσα;
Καλησπέρα!
Ευχαριστώ για τις επιπλέον ιδέες - λύσεις!
Κ. Δημήτρη κι εγώ έφτασα σε παρόμοια σχέση από το τύπο της διχοτόμου αλλά δεν κατάφερα να το ολοκληρώσω.
Προσπαθώ κι εγώ και προσδοκώ εν καιρώ μία καθαρά συνθετική λύση!
Συνεχίζουμε...
Υ.Γ. Αν κάποιος συνάδελφος έχει δει ξανά το θέμα σε κάποια βιβλιογραφία ας μας ενημερώσει! Ευχαριστώ και πάλι!
Ευχαριστώ για τις επιπλέον ιδέες - λύσεις!
Κ. Δημήτρη κι εγώ έφτασα σε παρόμοια σχέση από το τύπο της διχοτόμου αλλά δεν κατάφερα να το ολοκληρώσω.
Προσπαθώ κι εγώ και προσδοκώ εν καιρώ μία καθαρά συνθετική λύση!
Συνεχίζουμε...
Υ.Γ. Αν κάποιος συνάδελφος έχει δει ξανά το θέμα σε κάποια βιβλιογραφία ας μας ενημερώσει! Ευχαριστώ και πάλι!
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
