 , εφάπτονται στον κύκλο .Υπάρχει περίπτωση να επιτύχουμε την ισότητα των πράσινων γωνιών του σχήματος ;
, εφάπτονται στον κύκλο .Υπάρχει περίπτωση να επιτύχουμε την ισότητα των πράσινων γωνιών του σχήματος ;Υπάρχει περίπτωση ;
Συντονιστής: gbaloglou
Υπάρχει περίπτωση ;
 , εφάπτονται στον κύκλο .Υπάρχει περίπτωση να επιτύχουμε την ισότητα των πράσινων γωνιών του σχήματος ;
, εφάπτονται στον κύκλο .Υπάρχει περίπτωση να επιτύχουμε την ισότητα των πράσινων γωνιών του σχήματος ;Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Υπάρχει περίπτωση ;
Υπάρχει.
Όταν στείλουμε το
 στο άπειρο αριστερά, έχουμε
στο άπειρο αριστερά, έχουμε  . Σε αυτή την περίπτωση το
. Σε αυτή την περίπτωση το  τείνει στον βόρειο πόλο
τείνει στον βόρειο πόλο  του κύκλου, οπότε
του κύκλου, οπότε  . Έτσι έχουμε περιπτώσεις με
. Έτσι έχουμε περιπτώσεις με  .
.Αν αντιθέτως στείλουμε το
 στο
στο  , τότε
, τότε 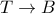 και άρα
και άρα  . Επίσης
. Επίσης  . Άρα έχουμε περιπτώσεις με
. Άρα έχουμε περιπτώσεις με  .
.Επειδή τα μεγέθη μεταβάλλονται κατά συνεχή τρόπο, κάπου θα έχουμε ισότητα.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Υπάρχει περίπτωση ;
Υπάρχει και υπολογίζεται και κατασκευάζεται: 
Μόλις βρω χρόνο, θα γράψω όλη τη λύση.

Μόλις βρω χρόνο, θα γράψω όλη τη λύση.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Υπάρχει περίπτωση ;
Έστω κύκλος  και τα εφαπτόμενα τμήματα
και τα εφαπτόμενα τμήματα 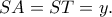 Είναι
Είναι 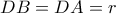 και
και 
Η τέμνει την
τέμνει την  στο
στο  όπου θέτω
όπου θέτω  Η
Η  τέμνει την
τέμνει την  στο
στο  Αρκεί να υπολογίσω το
Αρκεί να υπολογίσω το  Με Π.Θ στο
Με Π.Θ στο  έχω:
έχω: 
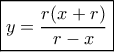

Από τα όμοια τρίγωνα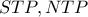 και
και  παίρνω:
παίρνω: 
απ' όπου χρησιμοποιώντας την μετά από πράξεις καταλήγω στην
μετά από πράξεις καταλήγω στην 
και παίρνω τη δεκτή ρίζα Το τμήμα
Το τμήμα  είναι κατασκευάσιμο, άρα
είναι κατασκευάσιμο, άρα
κατασκευάζεται και η γωνία της οποίας η εφαπτομένη δίνεται από τον τύπο της προηγούμενής μου ανάρτησης.
της οποίας η εφαπτομένη δίνεται από τον τύπο της προηγούμενής μου ανάρτησης.
 και τα εφαπτόμενα τμήματα
και τα εφαπτόμενα τμήματα 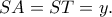 Είναι
Είναι 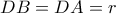 και
και 
Η
 τέμνει την
τέμνει την  στο
στο  όπου θέτω
όπου θέτω  Η
Η  τέμνει την
τέμνει την  στο
στο  Αρκεί να υπολογίσω το
Αρκεί να υπολογίσω το  Με Π.Θ στο
Με Π.Θ στο  έχω:
έχω: 
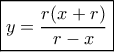

Από τα όμοια τρίγωνα
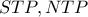 και
και  παίρνω:
παίρνω: 
απ' όπου χρησιμοποιώντας την
 μετά από πράξεις καταλήγω στην
μετά από πράξεις καταλήγω στην 
και παίρνω τη δεκτή ρίζα
 Το τμήμα
Το τμήμα  είναι κατασκευάσιμο, άρα
είναι κατασκευάσιμο, άρα κατασκευάζεται και η γωνία
 της οποίας η εφαπτομένη δίνεται από τον τύπο της προηγούμενής μου ανάρτησης.
της οποίας η εφαπτομένη δίνεται από τον τύπο της προηγούμενής μου ανάρτησης.- Γιώργος Μήτσιος
- Δημοσιεύσεις: 1789
- Εγγραφή: Κυρ Ιούλ 01, 2012 10:14 am
- Τοποθεσία: Aρτα
Re: Υπάρχει περίπτωση ;
Καλημέρα! Είδα την  και ..μπήκα, αφού πίσω της ..
και ..μπήκα, αφού πίσω της ..  ..κρύβεται ο χρυσός αριθμός
..κρύβεται ο χρυσός αριθμός  .
. , όπως το υπολόγισε ο Γιώργος όταν δίνεται το
, όπως το υπολόγισε ο Γιώργος όταν δίνεται το 
Η σχέση γράφεται και ως εξής: . Θέτω
. Θέτω  και
και 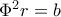 οπότε
οπότε  και
και  .
Στο σχήμα φαίνονται οι ορθές γωνίες και έχουμε
.
Στο σχήμα φαίνονται οι ορθές γωνίες και έχουμε  ,
,  ,
, 
ενώ και
και  . Παίρνουμε
. Παίρνουμε 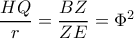
 .
.
Ακόμη
 άρα
άρα 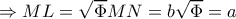 και
και  .
.
Τελικά συνεπώς το
συνεπώς το  είναι το ζητούμενο.
είναι το ζητούμενο.
Φιλικά, Γιώργος.
 και ..μπήκα, αφού πίσω της ..
και ..μπήκα, αφού πίσω της ..  .
.Μια προσπάθεια για την κατασκευή τουgeorge visvikis έγραψε: ↑Τρί Φεβ 16, 2021 12:21 pm
Έστω κύκλοςκαι τα εφαπτόμενα τμήματα
Είναι
και

Ητέμνει την
στο
όπου θέτω
Η
τέμνει την
στο
Αρκεί να υπολογίσω το

Με Π.Θ στοέχω:

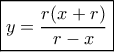
Από τα όμοια τρίγωνακαι
παίρνω:
απ' όπου χρησιμοποιώντας τηνμετά από πράξεις καταλήγω στην
και παίρνω τη δεκτή ρίζαΤο τμήμα
είναι κατασκευάσιμο, άρα
κατασκευάζεται και η γωνίατης οποίας η εφαπτομένη δίνεται από τον τύπο της προηγούμενής μου ανάρτησης.
 , όπως το υπολόγισε ο Γιώργος όταν δίνεται το
, όπως το υπολόγισε ο Γιώργος όταν δίνεται το 
Η σχέση γράφεται και ως εξής:
 . Θέτω
. Θέτω  και
και 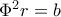 οπότε
οπότε  και
και  .
Στο σχήμα φαίνονται οι ορθές γωνίες και έχουμε
.
Στο σχήμα φαίνονται οι ορθές γωνίες και έχουμε  ,
,  ,
, 
ενώ
 και
και  . Παίρνουμε
. Παίρνουμε 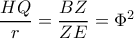
 .
. Ακόμη

 άρα
άρα 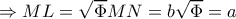 και
και  .
. Τελικά
 συνεπώς το
συνεπώς το  είναι το ζητούμενο.
είναι το ζητούμενο.Φιλικά, Γιώργος.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
