KARKAR έγραψε: ↑Σάβ Μαρ 05, 2022 1:54 pm
Εικαστική τέχνη.pngΟ κύκλος

, έχει το κέντρο του πάνω σε μεγαλύτερο κύκλο

, τον οποίο τέμνει
στα σημεία

. Ευθεία διερχόμενη από το

, τέμνει τους δύο κύκλους στα σημεία

.
Οι εφαπτόμενες των δύο κύκλων στα

τέμνονται στο σημείο

.
α) Εικασία : Το τμήμα

μεγιστοποιείται όταν :

.
β) Αποδεχόμενοι την εικασία και γνωρίζοντας ότι :

, υπολογίστε το

.
Πρώτα-πρώτα πάντα

.

- Εικαστική τέχνη_Ανάλυση_1.png (15.38 KiB) Προβλήθηκε 340 φορές
Πράγματι το τετράπλευρο

είναι εγγεγραμμένο και

άρα η

διχοτομεί τη γωνία του τετράπλευρου στο

.
Επί πλέον

( πάλι από τετράπλευρο

) και έτσι αβίαστα έχω ,

.

- Εικαστική τέχνη_Ανάλυση_2.png (28.94 KiB) Προβλήθηκε 340 φορές
Τώρα στην άσκηση , Επειδή

( υπό χορδής κι εφαπτομένης) και αφού στο

το άθροισμα των γωνιών του είναι

ορθές ,
στο τετράπλευρο

το άθροισμα των γωνιών του στα

θα είναι

ορθές άρα θα είναι εγγράψιμο .
Ο κύκλος του τετράπλευρου αυτού θα έχει το κέντρο του, έστω

, στην

. Αν η

τέμνει τον κύκλο αυτό (ακόμα) στο

θα έχει διάμετρο την

.
Επειδή η διαγώνιος

του τετράπλευρου

είναι εν γένει χορδή του κύκλου
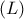
θα είναι

και έτσι η

παίρνει τη μέγιστη τιμή αν γίνει κι αυτή διάμετρος .
Τότε θα έχουμε :
.

- Εικαστική τέχνη_Ανάλυση_3_Υπολογισμοί.png (36.09 KiB) Προβλήθηκε 340 φορές
.
Τα

σε ευθεία καθώς και τα

. Επίσης το τετράπλευρο

θα είναι ορθογώνιο και το

ορθογώνιο στο ενώ


, ενώ η κοινή χορδή

θα είναι κάθετη στις

.
Αν τώρα

θα είναι

.
Στο ορθογώνιο τρίγωνο

ισχύουν :

 , έχει το κέντρο του πάνω σε μεγαλύτερο κύκλο
, έχει το κέντρο του πάνω σε μεγαλύτερο κύκλο  , τον οποίο τέμνει
, τον οποίο τέμνει  . Ευθεία διερχόμενη από το
. Ευθεία διερχόμενη από το  , τέμνει τους δύο κύκλους στα σημεία
, τέμνει τους δύο κύκλους στα σημεία  .
. τέμνονται στο σημείο
τέμνονται στο σημείο  .
. μεγιστοποιείται όταν :
μεγιστοποιείται όταν :  .
. , υπολογίστε το
, υπολογίστε το  .
.
 σημείο του τόξου του κύκλου
σημείο του τόξου του κύκλου  που δεν περιέχει το
που δεν περιέχει το  . Τότε είναι
. Τότε είναι 
 οπότε τα ισοσκελή τρίγωνα (από τις ακτίνες των κύκλων)
οπότε τα ισοσκελή τρίγωνα (από τις ακτίνες των κύκλων)  είναι όμοια , άρα
είναι όμοια , άρα 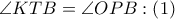
 και
και  .
. ομοκυκλικά και συνεπώς η
ομοκυκλικά και συνεπώς η  είναι χορδή κύκλου και άρα θα μεγιστοποιηθεί όταν γίνει διάμετρός του, δηλαδή όταν
είναι χορδή κύκλου και άρα θα μεγιστοποιηθεί όταν γίνει διάμετρός του, δηλαδή όταν  διάμετρος του κύκλου
διάμετρος του κύκλου  διάμετρος του
διάμετρος του  οπότε από το τρίγωνο
οπότε από το τρίγωνο  θα είναι
θα είναι  (συνδέει τα μέσα των δύο πλευρών του) και μάλιστα
(συνδέει τα μέσα των δύο πλευρών του) και μάλιστα 
 και άρα
και άρα  οπότε από τον τύπο του Ήρωνα θα έχουμε:
οπότε από τον τύπο του Ήρωνα θα έχουμε: 

 προκύπτει ότι τα ορθογώνια τρίγωνα
προκύπτει ότι τα ορθογώνια τρίγωνα  είναι όμοια και συνεπώς
είναι όμοια και συνεπώς  (μιλάμε για τη μέγιστη τιμή του
(μιλάμε για τη μέγιστη τιμή του  .
.
 είναι εγγεγραμμένο και
είναι εγγεγραμμένο και  άρα η
άρα η  διχοτομεί τη γωνία του τετράπλευρου στο
διχοτομεί τη γωνία του τετράπλευρου στο  .
. ( πάλι από τετράπλευρο
( πάλι από τετράπλευρο  .
. ( υπό χορδής κι εφαπτομένης) και αφού στο
( υπό χορδής κι εφαπτομένης) και αφού στο  το άθροισμα των γωνιών του είναι
το άθροισμα των γωνιών του είναι  ορθές ,
ορθές , το άθροισμα των γωνιών του στα
το άθροισμα των γωνιών του στα  θα είναι
θα είναι  , στην
, στην  θα έχει διάμετρο την
θα έχει διάμετρο την  .
.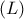 θα είναι
θα είναι  και έτσι η
και έτσι η  σε ευθεία καθώς και τα
σε ευθεία καθώς και τα  . Επίσης το τετράπλευρο
. Επίσης το τετράπλευρο  θα είναι ορθογώνιο και το
θα είναι ορθογώνιο και το  ορθογώνιο στο ενώ
ορθογώνιο στο ενώ 
 , ενώ η κοινή χορδή
, ενώ η κοινή χορδή  θα είναι κάθετη στις
θα είναι κάθετη στις  .
. θα είναι
θα είναι  .
.  ισχύουν :
ισχύουν : 