Γεια σας. Σας ευχαριστώ όλους για τις λύσεις σας.
Παραθέτω τρεις προσεγγίσεις που είχα ετοιμάσει. Όπως είναι φυσικό παρουσιάζουν ομοιότητες κα επικαλύψεις με άλλες που έχουν δοθεί. Η δεύτερη μοιάζει με μια που έδωσε στο fb ο συνάδελφος Γιάννης Πλατάρος ενώ η τρίτη με αυτή που έδωσε ο Γιώργος Μπαλόγλου πιο πάνω.
Α) Με συνθετική γεωμετρία.
Δίνω μόνο τα σχήματα μιας και οι αιτιολογήσεις είναι άμεσες. Η ισότητα των δύο εμβαδών στο τελευταίο στιγμιότυπο προκύπτει από το εγγράψιμμο

.
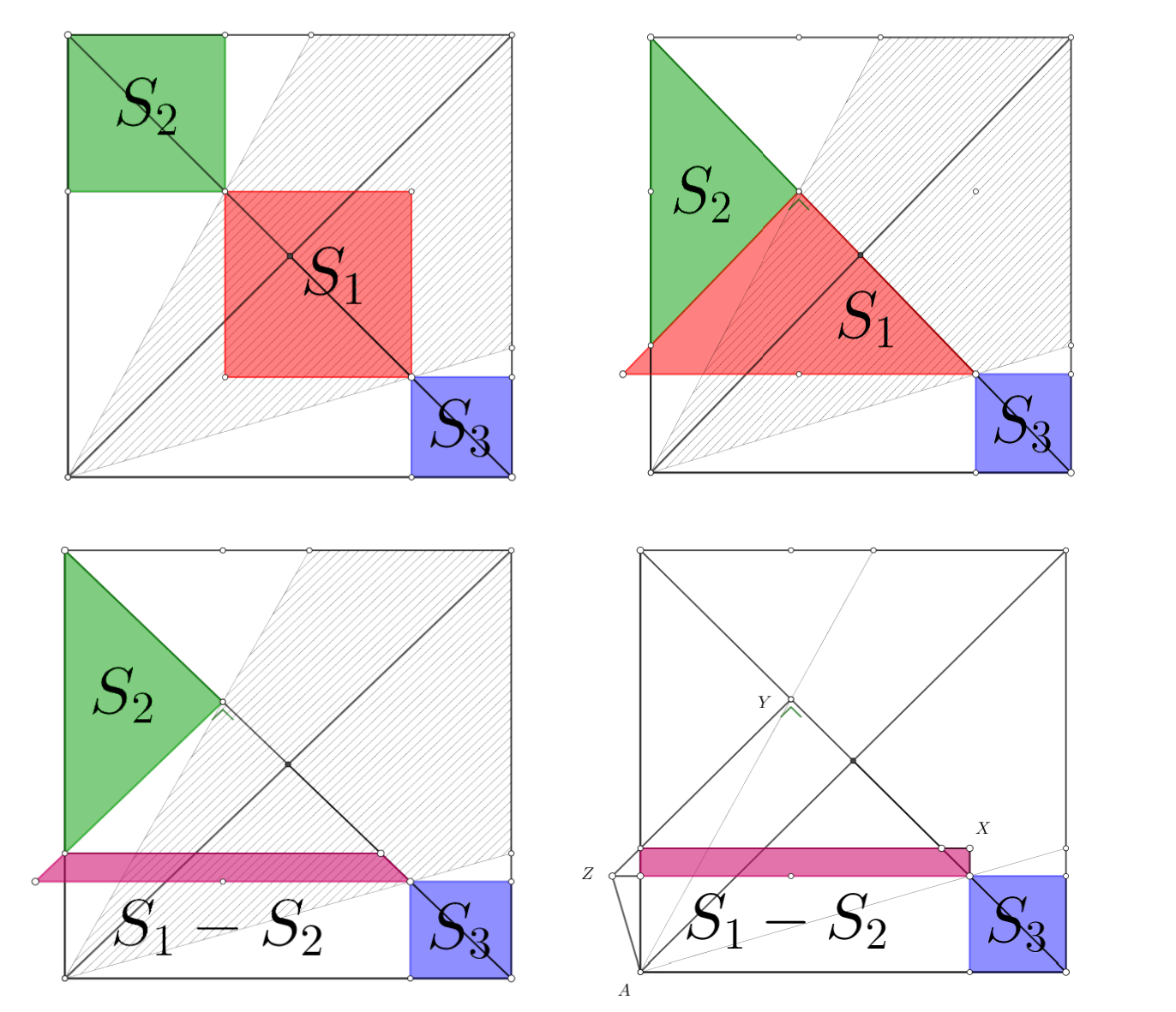
- Squares a.png (581.6 KiB) Προβλήθηκε 603 φορές
B) Με τριγωνομετρία.
Με
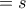
και

το μισό της διαγωνίου θέλουμε
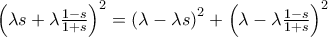
ή ισοδύναμα ότι
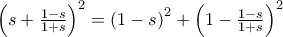
που η επαλήθευση της είναι άμεση.
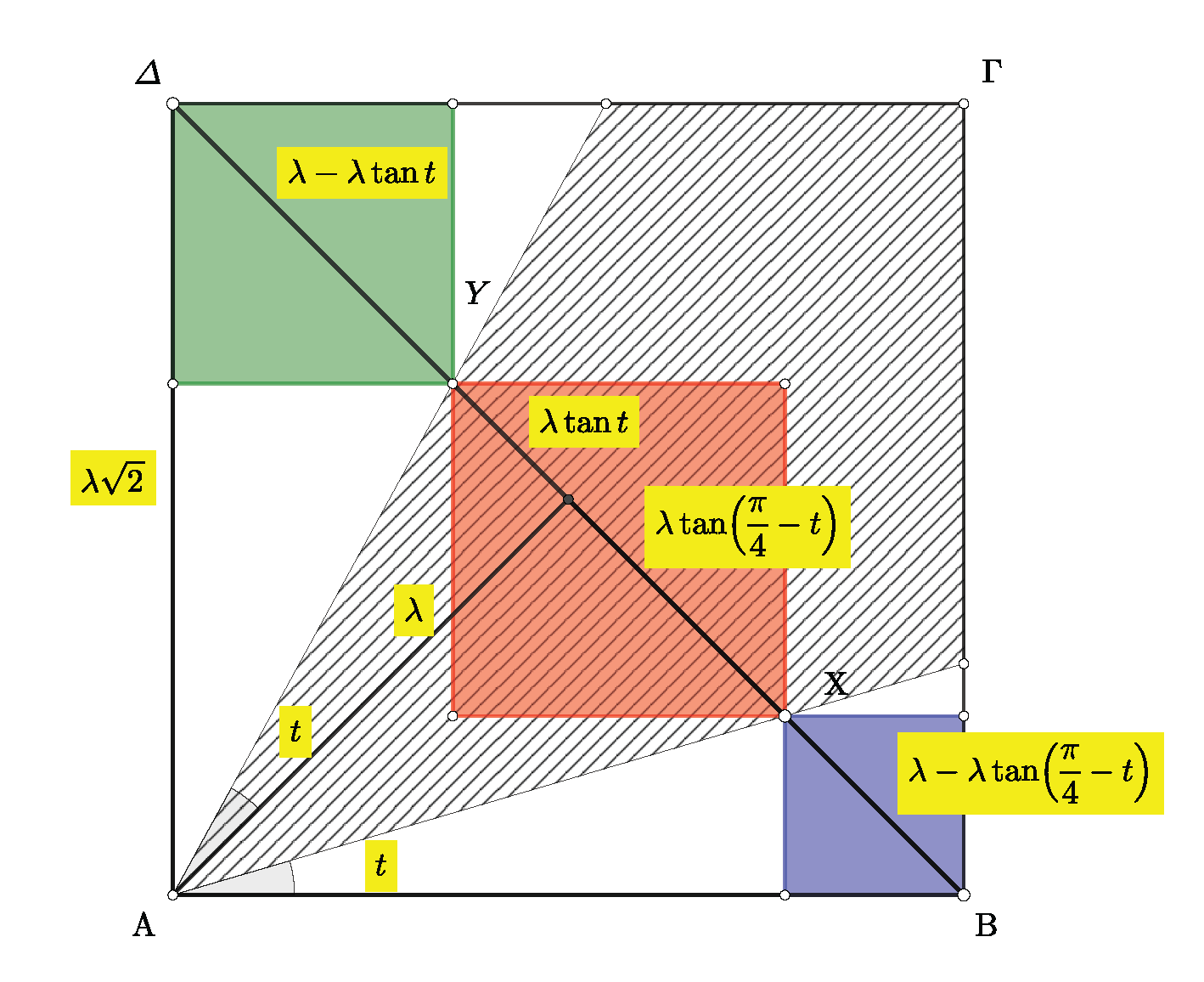
- Squares b.png (95.21 KiB) Προβλήθηκε 603 φορές
Γ) Με αναλυτική γεωμετρία.
Μπορούμε χωρίς βλάβη της γενικότητας να υποθέσουμε ότι το αρχικό τετράγωνο έχει πλευρά

οπότε αποδίδοντας συντεταγμένες στις κορυφές του και στα

,

έχουμε το σχήμα
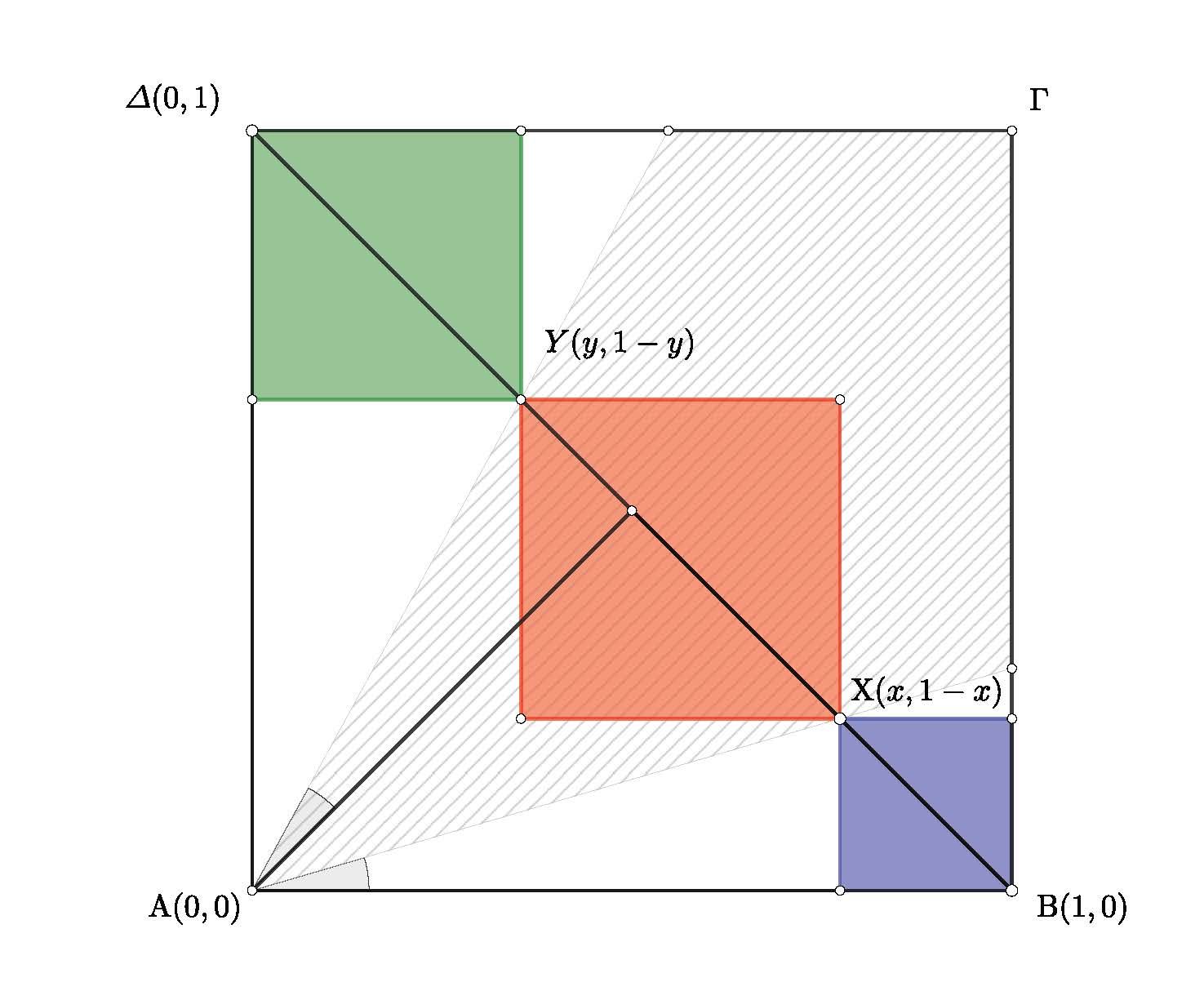
- Squares c.jpg (104.84 KiB) Προβλήθηκε 603 φορές
Αν ονομάσουμε

,

τους συντελεστές διευθύνσεως των

,

έχουμε
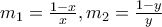
και αφού
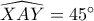
είναι
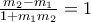
.
Αντικαθιστώντας στην τελευταία και λύνονας ως προς

βρίσκουμε
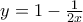
Είναι
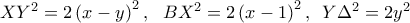
και θέλουμε
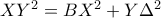
που επαληθεύεται άμεσα με αντικατάσταση των

και
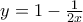
.
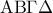 . Γωνία
. Γωνία 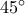 με κορυφή το
με κορυφή το 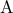 περιέχεται στην
περιέχεται στην 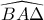 και οι πλευρές της τέμνουν την διαγώνιο
και οι πλευρές της τέμνουν την διαγώνιο 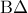 στα
στα 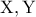 (
(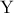 μεταξύ
μεταξύ 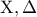 ). Να αποδειχθεί ότι το εμβαδόν του τετραγώνου με διαγώνιο
). Να αποδειχθεί ότι το εμβαδόν του τετραγώνου με διαγώνιο 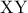 είναι ίσο με το άθροισμα των εμβαδών των τετραγώνων με διαγωνίους τις
είναι ίσο με το άθροισμα των εμβαδών των τετραγώνων με διαγωνίους τις 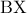 ,
, 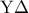 .
.
 η κάτω αριστερή κορυφή του κόκκινου τετραγώνου. Ο περιγεγραμμένος κύκλος του τριγώνου
η κάτω αριστερή κορυφή του κόκκινου τετραγώνου. Ο περιγεγραμμένος κύκλος του τριγώνου  θα έχει κέντρο το
θα έχει κέντρο το 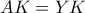 . Έστω τώρα
. Έστω τώρα  η προβολή του
η προβολή του  . Τότε από ΠΘ στο
. Τότε από ΠΘ στο  έχουμε το ζητούμενο.
έχουμε το ζητούμενο.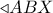 κατά
κατά  αριστερά από το σημείο
αριστερά από το σημείο 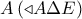 .
.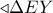 είναι ορθογώνιο με υποτείνουσα την
είναι ορθογώνιο με υποτείνουσα την 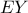 , η οποία είναι ίση με την
, η οποία είναι ίση με την  από την ισότητα των
από την ισότητα των 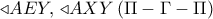 και η απόδειξη ολοκληρώνεται.
και η απόδειξη ολοκληρώνεται.
![= [(Y\Delta^2 + (B\Delta - Y\Delta)^2) + ((B\Delta-XB)^2+ XB^2) ]/2- 4*(XY*B\Delta/2)/2 = (Y\Delta)^2 + (XB)^2 = [(Y\Delta^2 + (B\Delta - Y\Delta)^2) + ((B\Delta-XB)^2+ XB^2) ]/2- 4*(XY*B\Delta/2)/2 = (Y\Delta)^2 + (XB)^2](/forum/ext/geomar/texintegr/latexrender/pictures/efa3a76335b8be3fd73aa7d02e75a8ea.png)

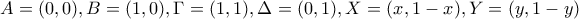 και εφαρμόζοντας Νόμο Συνημιτόνων στο
και εφαρμόζοντας Νόμο Συνημιτόνων στο 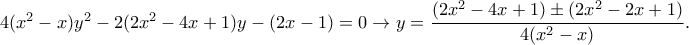
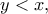 οπότε επιλέγουμε υποχρεωτικά το
οπότε επιλέγουμε υποχρεωτικά το  καταλήγοντας στην
καταλήγοντας στην 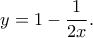
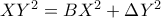 είναι ισοδύναμη προς την
είναι ισοδύναμη προς την 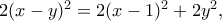 η οποία είναι άμεση από την παραπάνω
η οποία είναι άμεση από την παραπάνω  .
.
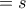 και
και  το μισό της διαγωνίου θέλουμε
το μισό της διαγωνίου θέλουμε 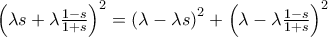
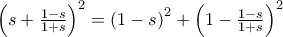
 οπότε αποδίδοντας συντεταγμένες στις κορυφές του και στα
οπότε αποδίδοντας συντεταγμένες στις κορυφές του και στα  ,
,  έχουμε το σχήμα
έχουμε το σχήμα
 ,
,  τους συντελεστές διευθύνσεως των
τους συντελεστές διευθύνσεως των  ,
,  έχουμε
έχουμε 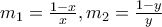 και αφού
και αφού 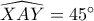 είναι
είναι 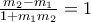 .
. βρίσκουμε
βρίσκουμε 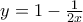
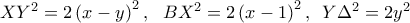
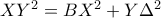
 και
και