 ενός ημικυκλίου βρίσκονται τα σταθερά σημεία
ενός ημικυκλίου βρίσκονται τα σταθερά σημεία  . Σημείο
. Σημείο  κινείται
κινείται στο ημικύκλιο . Εικάζεται ότι η γωνία
 μεγιστοποιείται , όταν οι
μεγιστοποιείται , όταν οι 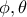 καταστούν ίσες ...
καταστούν ίσες ... Συντονιστής: gbaloglou
 ενός ημικυκλίου βρίσκονται τα σταθερά σημεία
ενός ημικυκλίου βρίσκονται τα σταθερά σημεία  . Σημείο
. Σημείο  κινείται
κινείται  μεγιστοποιείται , όταν οι
μεγιστοποιείται , όταν οι 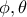 καταστούν ίσες ...
καταστούν ίσες ... Καταρχάς ας δούμε τον προσδιορισμό του
 , ώστε
, ώστε 
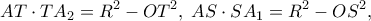
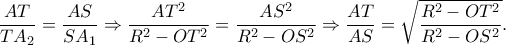
 προσδιορίζεται ως τομή του αρχικού κύκλου και του Απολλώνιου κύκλου με βάση το τμήμα
προσδιορίζεται ως τομή του αρχικού κύκλου και του Απολλώνιου κύκλου με βάση το τμήμα 
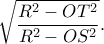
 εφάπτεται στον αρχικό κύκλο (και είναι εκείνος με την ελάχιστη ακτίνα σε σύγκριση με τις ακτίνες των περιγεγραμμένων κύκλων στα τρίγωνα με ίδια βάση και κορυφή τυχόν σημείο του πάνω ημικυκλίου διαφορετικού του
εφάπτεται στον αρχικό κύκλο (και είναι εκείνος με την ελάχιστη ακτίνα σε σύγκριση με τις ακτίνες των περιγεγραμμένων κύκλων στα τρίγωνα με ίδια βάση και κορυφή τυχόν σημείο του πάνω ημικυκλίου διαφορετικού του  ). Προφανώς είναι καθαρό ότι ισχύει
). Προφανώς είναι καθαρό ότι ισχύει 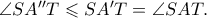
 είναι επίσης εφικτός με βάση την Απολλώνια κατασκευή κύκλου διερχόμενου από τα σημεία
είναι επίσης εφικτός με βάση την Απολλώνια κατασκευή κύκλου διερχόμενου από τα σημεία  και εφαπτόμενου στον δοθέντα κύκλο της διαμέτρου δηλαδή
και εφαπτόμενου στον δοθέντα κύκλο της διαμέτρου δηλαδή 
 . Αν ονομάσουμε
. Αν ονομάσουμε  το σημείο επαφής, τότε οι
το σημείο επαφής, τότε οι  , οπότε από την ισότητα των γωνιών εγγεγραμμένης με την υπό χορδής και εφαπτομένης προκύπτει
, οπότε από την ισότητα των γωνιών εγγεγραμμένης με την υπό χορδής και εφαπτομένης προκύπτει 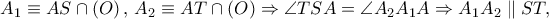 επομένως
επομένως 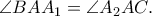
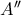 σημείο του αρχικού κύκλου και ονομάσουμε
σημείο του αρχικού κύκλου και ονομάσουμε 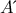 την τομή των
την τομή των 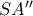 με τον κύκλο
με τον κύκλο 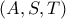
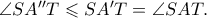
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες