Υποθέτοντας ότι σε κάθε κορυφή του Αρχιμήδειου στερεού συναντώνται
 τρίγωνα,
τρίγωνα,  τετράγωνα,
τετράγωνα,  πεντάγωνα, κοκ ... συμπεραίνουμε ότι ο αριθμός των πλευρών του στερεού ισούται προς
πεντάγωνα, κοκ ... συμπεραίνουμε ότι ο αριθμός των πλευρών του στερεού ισούται προς ![\dfrac{\gamma}{3}V +\dfrac{\delta}{4}V +\dfrac{\epsilon}{5}V +...=\left[\dfrac{\gamma}{3} +\dfrac{\delta}{4} +\dfrac{\epsilon}{5} +...\right]V \dfrac{\gamma}{3}V +\dfrac{\delta}{4}V +\dfrac{\epsilon}{5}V +...=\left[\dfrac{\gamma}{3} +\dfrac{\delta}{4} +\dfrac{\epsilon}{5} +...\right]V](/forum/ext/geomar/texintegr/latexrender/pictures/a17440f7128be4731a0d7506a1547919.png) και ο αριθμός των ακμών του στερεού ισούται προς
και ο αριθμός των ακμών του στερεού ισούται προς 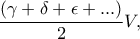 όπου
όπου  ο αριθμός των κορυφών του στερεού. Άμεσα ο τύπος του Euler δίνει
ο αριθμός των κορυφών του στερεού. Άμεσα ο τύπος του Euler δίνει![\left[1+\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\gamma +\left(\dfrac{1}{4}-\dfrac{1}{2}\right)\delta +\left(\dfrac{1}{5}-\dfrac{1}{2}\right)\epsilon +...\right]V=2
\left[1+\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\gamma +\left(\dfrac{1}{4}-\dfrac{1}{2}\right)\delta +\left(\dfrac{1}{5}-\dfrac{1}{2}\right)\epsilon +...\right]V=2](/forum/ext/geomar/texintegr/latexrender/pictures/01ea6e1651aa03f394d237fe17249e2e.png)
Γνωρίζουμε ήδη από τον κατάλογο των Αρχιμήδειων στερεών ότι δεν μπορούμε να πάμε πέρα από τα δεκάγωνα: δεν βλέπω (!) πως θα μπορούσαμε να αποκλείσουμε ενδεκάγωνα κλπ 'εκ των προτέρων', ώστε η παραπάνω διοφαντική εξίσωση να 'περατωθεί', και να έχουμε ακριβώς οκτώ ακέραιες μεταβλητές (
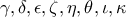 ). Ακόμη και αν επιτευχθεί αυτό, η προκύπτουσα πεπερασμένη διοφαντική εξίσωση
). Ακόμη και αν επιτευχθεί αυτό, η προκύπτουσα πεπερασμένη διοφαντική εξίσωση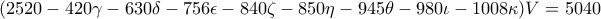
είναι 'πολλαπλή' ... με την έννοια ότι προκύπτει μία διοφαντική εξίσωση για κάθε έναν από τους 60 διαιρέτες του 5040!
[Δεν είναι πάντως και τόσο τρομερό όσο ακούγεται στην εποχή των ΗΥ (για να μην αναφέρω και την πανταχού παρούσα πλέον ΑΙ)

![\left[1+0 +0 + 1\cdot\left(\dfrac{1}{5}-\dfrac{1}{2}\right) + 2\cdot\left(\dfrac{1}{6}-\dfrac{1}{2}\right)+ 0 \right]V=2 \left[1+0 +0 + 1\cdot\left(\dfrac{1}{5}-\dfrac{1}{2}\right) + 2\cdot\left(\dfrac{1}{6}-\dfrac{1}{2}\right)+ 0 \right]V=2](/forum/ext/geomar/texintegr/latexrender/pictures/49fae446bbb8c294634578e9662f3d8c.png)