Εξίσωση με ισοτιμία

bouzoukman · #1

Αποδείξτε ότι το πλήθος των λύσεων της ισοτιμίας

$\displaystyle{ x^2 + y^2 \equiv 1\pmod{p}, }$

με 0 < x < p

,

και

περιττός πρώτο, είναι άρτιος αριθμός αν και μόνο αν $p\equiv \pm 3 \pmod{24}$ .

stranger · #2

ΛΑΘΟΣ POST

stranger · #3

Θα δείξω ότι το πλήθος

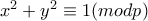των λύσεων της $x^2+y^2 \equiv 1 (mod p)$ είναι άρτιο για κάθε περιττό πρώτο

.
Έστω $A=\{(x,y) : x^2 + y^2 \equiv 1(mod p), 0<x<p,0<y<p, x<y\}$ και $B=\{(x,y) : x^2 + y^2 \equiv 1(mod p), 0<x<p,0<y<p, y<x\}$
Τότε η συνάρτηση $f: A \rightarrow B$ με f(x,y)=(y,x)

είναι ένα προς ένα και επί.
Άρα |A|=|B|

.
Επίσης, είναι εύκολο να δούμε ότι αν (x,x)

είναι λύση τότε (p-x,p-x)

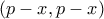είναι επίσης λύση της ισοτιμίας 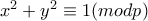$x^2+y^2 \equiv 1 (mod p)$ με 0<x<p, 0<y<p

ώστε

, οπότε αν υπάρχει λύση της παραπάνω ισοτιμίας με (x,y)

με

τότε υπάρχουν υπάρχουν ακριβώς δύο τέτοιες.
Παίρνουμε περιπτώσεις.
Αν δεν υπάρχει

ώστε το

να είναι λύση τότε το πλήθος είναι w= |A|+|B|=2|A|

, οπότε ο

είναι άρτιος.
Αν υπάρχει

ώστε το

να είναι λύση τότε w= |A|+|B|+2=2|A|+2

, οπότε πάλι ο

είναι άρτιος και το συμπέρασμα έπεται.

Εξίσωση με ισοτιμία

Εξίσωση με ισοτιμία

Re: Εξίσωση με ισοτιμία

Re: Εξίσωση με ισοτιμία

Μέλη σε σύνδεση