 όπου
όπου  . Να αποδειχθούν τα παρακάτω:
. Να αποδειχθούν τα παρακάτω:-
![[K:\mathbb{Q}]=3 [K:\mathbb{Q}]=3](/forum/ext/geomar/texintegr/latexrender/pictures/6ff8284d3181c6e71fdf5a9f8e0fbf4b.png) .
. - Η επέκταση
 είναι Galois.
είναι Galois. - Ένα πρώτος
 splits completely (διασπάται πλήρως(;)) σε γινόμενο πρώτων ιδεωδών στο
splits completely (διασπάται πλήρως(;)) σε γινόμενο πρώτων ιδεωδών στο  αν και μόνο αν
αν και μόνο αν  .
.
Συντονιστής: nkatsipis
 όπου
όπου  . Να αποδειχθούν τα παρακάτω:
. Να αποδειχθούν τα παρακάτω:![[K:\mathbb{Q}]=3 [K:\mathbb{Q}]=3](/forum/ext/geomar/texintegr/latexrender/pictures/6ff8284d3181c6e71fdf5a9f8e0fbf4b.png) .
. είναι Galois.
είναι Galois. splits completely (διασπάται πλήρως(;)) σε γινόμενο πρώτων ιδεωδών στο
splits completely (διασπάται πλήρως(;)) σε γινόμενο πρώτων ιδεωδών στο  αν και μόνο αν
αν και μόνο αν  .
. .
.Σωστός! Για κάποια πράγματα δεν ξέρω την ελληνική ορολογία. Αυτό που θέλω να πω είναι ότι ο '
 splits completely'.
splits completely'. είναι τρίτου βαθμού είναι αρκετό να δείξουμε ότι δεν έχει ρίζα στο
είναι τρίτου βαθμού είναι αρκετό να δείξουμε ότι δεν έχει ρίζα στο  (σχετικά γνωστή πρόταση!). Έστω
(σχετικά γνωστή πρόταση!). Έστω  , με
, με  και
και  , μία ρίζα του
, μία ρίζα του  . Τότε ισχύει
. Τότε ισχύει
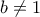 τότε από την τελευταία ισότητα έχουμε ότι οποιοδήποτε πρώτος
τότε από την τελευταία ισότητα έχουμε ότι οποιοδήποτε πρώτος  που διαιρεί το
που διαιρεί το  διαιρεί το
διαιρεί το  που έρχεται σε αντίθεση με το γεγονός ότι
που έρχεται σε αντίθεση με το γεγονός ότι  . Άρα
. Άρα  και
και  . Πάλι από την σχέση
. Πάλι από την σχέση 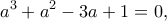
 άρα
άρα  . Εφόσον
. Εφόσον 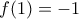 και
και  το
το  δεν έχει ρίζες στο
δεν έχει ρίζες στο  άρα είναι ανάγωγο. Οπότε
άρα είναι ανάγωγο. Οπότε ![[K:\mathbb{Q}]=3 [K:\mathbb{Q}]=3](/forum/ext/geomar/texintegr/latexrender/pictures/6ff8284d3181c6e71fdf5a9f8e0fbf4b.png) .
. οι τρεις ρίζες του
οι τρεις ρίζες του  . Ορίζουμε
. Ορίζουμε  , τότε από Θεωρία Galois γνωρίζουμε ότι η επέκταση
, τότε από Θεωρία Galois γνωρίζουμε ότι η επέκταση  είναι Galois και από το ερώτημα (1) έχουμε ότι
είναι Galois και από το ερώτημα (1) έχουμε ότι  ή
ή  . Ας υποθέσουμε ότι
. Ας υποθέσουμε ότι  , τότε η ποσότητα
, τότε η ποσότητα
 , άρα
, άρα  . Οπότε
. Οπότε  . Όμως από τον ορισμό της ορίζουσας του
. Όμως από τον ορισμό της ορίζουσας του  έχουμε ότι
έχουμε ότι  . Από γνωστούς τύπους (ή με χρήση υπολογιστή όπως εγώ) βλέπουμε ότι
. Από γνωστούς τύπους (ή με χρήση υπολογιστή όπως εγώ) βλέπουμε ότι  , πράγμα που αναιρεί το γεγονός ότι
, πράγμα που αναιρεί το γεγονός ότι  . Επομένως καταλήγουμε ότι
. Επομένως καταλήγουμε ότι  και
και  , άρα
, άρα  είναι Galois.
είναι Galois. είναι Galois,
είναι Galois, ![[K:\mathbb{Q}]=3 [K:\mathbb{Q}]=3](/forum/ext/geomar/texintegr/latexrender/pictures/6ff8284d3181c6e71fdf5a9f8e0fbf4b.png) και
και  καταλαβαίνουμε ότι
καταλαβαίνουμε ότι  . Έστω
. Έστω 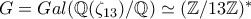 και
και  . Επειδή η τάξη της
. Επειδή η τάξη της  είναι
είναι  καταλαβαίνουμε από θεωρία Galois ότι
καταλαβαίνουμε από θεωρία Galois ότι  . Από γνωστό θεώρημα για τα κυκλοτομικά σώματα αριθμών έχουμε ότι ένας πρώτος
. Από γνωστό θεώρημα για τα κυκλοτομικά σώματα αριθμών έχουμε ότι ένας πρώτος 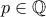 παραγοντοποιείται σε γινόμενο τριών πρώτων ιδεωδών στο
παραγοντοποιείται σε γινόμενο τριών πρώτων ιδεωδών στο  αν και μόνο αν
αν και μόνο αν  . Επειδή
. Επειδή  έχουμε το ζητούμενο.
έχουμε το ζητούμενο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης