Πρόβλημα : Θεωρούμε τους θετικούς ακέραιους αριθμούς
 τέτοιους ώστε να ικανοποιούν την συνθήκη ότι ο αριθμός
τέτοιους ώστε να ικανοποιούν την συνθήκη ότι ο αριθμός  είναι επίσης θετικός ακέραιος. Τότε να δειχθεί ότι ο αριθμός
είναι επίσης θετικός ακέραιος. Τότε να δειχθεί ότι ο αριθμός  είναι αριθμός
είναι αριθμός 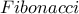 .
.Λύση
Αρχικά μπορούμε να υποθέσουμε χωρίς βλάβη της γενικότητας
 . Tότε έχουμε τις εξής δύο περιπτώσεις
. Tότε έχουμε τις εξής δύο περιπτώσειςΑν
 τότε προκύπτει ότι
τότε προκύπτει ότι ή
ή 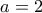
, και τότε για
 είναι
είναι 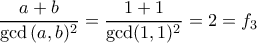 , επιπλέον για
, επιπλέον για 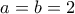 είναι
είναι  .
.Αν
 και άρα
και άρα  τότε εξ' υποθέσεως έχουμε ότι υπάρχει θετικός ακέραιος
τότε εξ' υποθέσεως έχουμε ότι υπάρχει θετικός ακέραιος  τέτοιος ώστε
τέτοιος ώστε  τότε ισοδύναμα έχουμε ότι:
τότε ισοδύναμα έχουμε ότι:
Έπειτα η σχέση (1) μας οδηγεί στο να θεωρήσουμε την δευτεροβάθμια εξίσωση (τριώνυμο)
 , την οποία επιλύουμε ως προς το
, την οποία επιλύουμε ως προς το  . Λόγω της σχέσης (1) έχουμε ότι η δευτεροβαθμία εξίσωση (2) έχει μια λύση η οποία είναι η
. Λόγω της σχέσης (1) έχουμε ότι η δευτεροβαθμία εξίσωση (2) έχει μια λύση η οποία είναι η  και μια δεύτερη λύση την
και μια δεύτερη λύση την  , τότε από τους τύπους
, τότε από τους τύπους 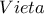 έχουμε ότι
έχουμε ότι  και
και  , τότε προκύπτει ότι
, τότε προκύπτει ότι  , και επειδή
, και επειδή  και άρα
και άρα 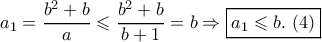 , σημειώνουμε ότι το
, σημειώνουμε ότι το  ικανοποιεί την εξίσωση (1), δηλαδή έχουμε ότι
ικανοποιεί την εξίσωση (1), δηλαδή έχουμε ότι  , τότε αν υποθέσουμε ότι το ζεύγος
, τότε αν υποθέσουμε ότι το ζεύγος  έχει το μικρότερο δυνατό άθροισμα ώστε ο αριθμός
έχει το μικρότερο δυνατό άθροισμα ώστε ο αριθμός  να είναι θετικός ακέραιος, τότε υπάρχει το ζεύγος
να είναι θετικός ακέραιος, τότε υπάρχει το ζεύγος  ώστε να ισχύει πως ο αριθμός
ώστε να ισχύει πως ο αριθμός 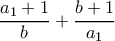 να είναι θετικός ακέραιος με την ιδιότητα ότι
να είναι θετικός ακέραιος με την ιδιότητα ότι  , το οποίο μας οδηγεί στο ότι πρέπει να ισχύει
, το οποίο μας οδηγεί στο ότι πρέπει να ισχύει  . Δηλαδή το σύνολο
. Δηλαδή το σύνολο  είναι μη κενό και υπάρχει ζεύγος
είναι μη κενό και υπάρχει ζεύγος  με
με  ώστε το
ώστε το 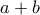 να είναι το ελάχιστο δυνατό μόνο στην περίπτωση που ισχύει ότι
να είναι το ελάχιστο δυνατό μόνο στην περίπτωση που ισχύει ότι  , τότε όμως θα ικανοποιείται η σχέση
, τότε όμως θα ικανοποιείται η σχέση  και
και  και άρα θα πρέπει
και άρα θα πρέπει  ή
ή 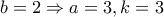 .
.Συμπέρασμα : Δοθέντος ενός ζεύγους
 , με
, με  , προκύπτει ο αριθμός
, προκύπτει ο αριθμός  , όπου για αυτόν τον αριθμό
, όπου για αυτόν τον αριθμό  αντιστοιχεί ένα ζεύγος
αντιστοιχεί ένα ζεύγος  με ελάχιστο άθροισμα, όπου τελικά για το ζεύγος με το ελάχιστο άθροισμα ισχύει
με ελάχιστο άθροισμα, όπου τελικά για το ζεύγος με το ελάχιστο άθροισμα ισχύει  και οπότε
και οπότε  ή
ή  . Οπότε οι μόνες δυνατές τιμές του
. Οπότε οι μόνες δυνατές τιμές του  είναι
είναι  ή
ή  .
.Τότε αν
 προκύπτει ότι ή
προκύπτει ότι ή : και άρα θα είναι
: και άρα θα είναι 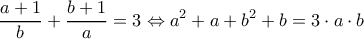 και ας είναι
και ας είναι  , τότε
, τότε  και
και  και τότε είναι
και τότε είναι  οπότε ισοδύναμα έχουμε ότι
οπότε ισοδύναμα έχουμε ότι 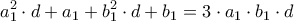 , και θέλουμε να υπολογίσουμε το
, και θέλουμε να υπολογίσουμε το  , (ΠΩΣ ΑΠΟΔΕΙΚΝΎΕΤΑΙ ΌΤΙ ΕΊΝΑΙ ΑΡΙΘΜΌΣ
, (ΠΩΣ ΑΠΟΔΕΙΚΝΎΕΤΑΙ ΌΤΙ ΕΊΝΑΙ ΑΡΙΘΜΌΣ 
 )
)ή
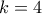 : και άρα θα είναι
: και άρα θα είναι  και ας είναι
και ας είναι  , τότε
, τότε  και
και 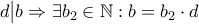 και τότε είναι
και τότε είναι  οπότε ισοδύναμα έχουμε ότι
οπότε ισοδύναμα έχουμε ότι  , και θέλουμε να υπολογίσουμε το
, και θέλουμε να υπολογίσουμε το  , (ΠΩΣ ΑΠΟΔΕΙΚΝΎΕΤΑΙ ΌΤΙ ΕΊΝΑΙ ΑΡΙΘΜΌΣ
, (ΠΩΣ ΑΠΟΔΕΙΚΝΎΕΤΑΙ ΌΤΙ ΕΊΝΑΙ ΑΡΙΘΜΌΣ 
 )
)Ερώτημα :
(1) Αν
 με
με  ή ισοδύναμα προκύπτει ότι για
ή ισοδύναμα προκύπτει ότι για  έχουμε ότι
έχουμε ότι  αλλά πως προκύπτει ότι ο αριθμός
αλλά πως προκύπτει ότι ο αριθμός  είναι αριθμός
είναι αριθμός 

(2) Αν
 με
με  (υπάρχει κάποια αντίστοιχη γραφεί με αυτή στο Ερώτημα (1), παρατηρείτε κάτι τέτοιο
(υπάρχει κάποια αντίστοιχη γραφεί με αυτή στο Ερώτημα (1), παρατηρείτε κάτι τέτοιο  ) ή ισοδύναμα προκύπτει ότι για
) ή ισοδύναμα προκύπτει ότι για  έχουμε ότι
έχουμε ότι 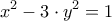 αλλά πως προκύπτει ότι ο αριθμός
αλλά πως προκύπτει ότι ο αριθμός  είναι αριθμός
είναι αριθμός 


 είναι
είναι  ή
ή 
 υπάρχουν άπειρα ζεύγη της μορφής
υπάρχουν άπειρα ζεύγη της μορφής 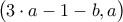 με αρχικό ζεύγος
με αρχικό ζεύγος  και έπειτα με διαδοχικές επαναλήψεις έχουμε :
και έπειτα με διαδοχικές επαναλήψεις έχουμε : 
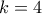 υπάρχουν άπειρα ζεύγη της μορφής
υπάρχουν άπειρα ζεύγη της μορφής  με αρχικό ζεύγος
με αρχικό ζεύγος  και έπειτα με διαδοχικές επαναλήψεις έχουμε :
και έπειτα με διαδοχικές επαναλήψεις έχουμε : 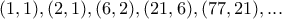
 και το έβαλα και στη διακρίνουσα.
και το έβαλα και στη διακρίνουσα.