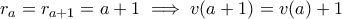Ερώτηση σχετικά με τους p-αριθμούς που σχετίζονται με το τελευταίο θεώρημα του Fermat.

Συντονιστής: nkatsipis

Πρώτη μη αναγνωσμένη δημοσίευση • 1 δημοσίευση • Σελίδα 1 από 1

Δαμιανός: Δημοσιεύσεις: 6; Εγγραφή: Παρ Νοέμ 24, 2023 11:52 am

Ερώτηση σχετικά με τους p-αριθμούς που σχετίζονται με το τελευταίο θεώρημα του Fermat.

Παράθεση

Μη αναγνωσμένη δημοσίευση από Δαμιανός » Κυρ Νοέμ 26, 2023 4:33 pm

Έχω μια ερώτηση σχετικά με τους p-αριθμούς που σχετίζονται με το τελευταίο θεώρημα του Fermat.

Ας:

$\displaystyle{x^p = y^p + z^p}$
$\displaystyle{ \gcd(x,y,z) = 1}$
$\displaystyle{xyz \not \equiv 0 \pmod p}$
$\displaystyle{x^{p-1} \equiv y^{p-1} \equiv z^{p-1} \equiv 1 \pmod{p^3}}$

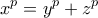
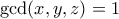
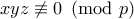
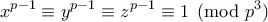
Σημείωση:

$\displaystyle{\frac{x^{p+1}-y^{p+1}}{x-y} = (p+1)x^p+a(x-y) \equiv x+y \pmod{p^3}}$
$\displaystyle{\frac{x^{p+1}-z^{p+1}}{x-z} = (p+1)x^p+b(x-z) \equiv x+z \pmod{p^3}}$
$\displaystyle{x \equiv y+z \pmod{p^3}}$

$\implies$

$\displaystyle{az \equiv y-px \pmod{p^3}}$
$\displaystyle{by \equiv z-px \pmod{p^3}}$

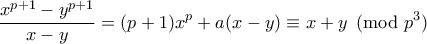
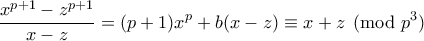
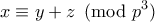
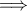
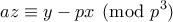
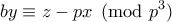
Μετά από μαθηματικές μετατροπές:

$\displaystyle{(a+1)^p-a^p-1 \equiv (b+1)^p-b^p-1 \equiv 0 \pmod{p^3}}$

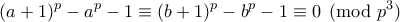
Υπολογισμός Fermat-quotients για a,a+1

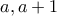(από συμμετρία μπορεί να χρησιμοποιηθεί και για το

):

$\displaystyle{z(a+1) \equiv y+z-px \equiv x(1-p) \pmod{p^3}}$

$\implies$

$\displaystyle{(a+1)^{p-1} \equiv (1-p)^{p-1} \equiv 1+p \pmod{p^3}}$

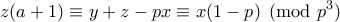
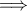
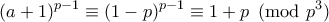
Και:

$\displaystyle{a^{p-1} \equiv 1+p\left(\frac{a+1}{a}\right) \pmod{p^3}}$

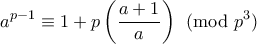
***Ερώτηση:***

Είδα στο κείμενο: *Σχετικά με Συνόρθωση με την Πρώτη Περίπτωση του Τελευταίου Θεωρήματος του Fermat* από τον Wells-Johnson, το οποίο ασχολείται με τους p-αριθμούς, ότι τα παραπάνω οδηγούν σε:

$\displaystyle{v(a+1) \equiv (a+1)^{p^{n+1}} \equiv (a+1)^{p^n} + r_{a+1}p^{n+1} \pmod{p^{n+2}}}$
$\displaystyle{v(a) \equiv a^{p^{n+1}} \equiv a^{p^n} + r_{a}p^{n+1} \pmod{p^{n+2}}}$

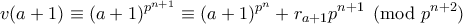
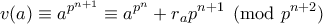
με $r_a = r_{a+1} = a+1$

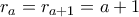
Που θα έπρεπε (αυτό είναι η ερώτησή μου):

$\displaystyle{v(a+1)=v(a)+1}$

$\implies$

$\displaystyle{a^2+a+1 \equiv 0 \pmod{p}}$

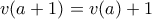
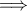
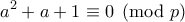
με $a \equiv y/z \pmod{p}$ .

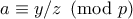Αυτό θα οδηγούσε σε δύο λύσεις a,b

:

$\displaystyle{a \equiv -\frac{p+1+(p-1)\sqrt{-3}}{2} \pmod{p^3}}$
$\displaystyle{b \equiv -\frac{p+1-(p-1)\sqrt{-3}}{2} \pmod{p^3}}$

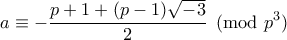
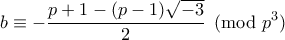
και σημαίνει: 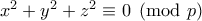$x^2+y^2+z^2 \equiv 0 \pmod{p}$ στην πρώτη περίπτωση του τελευταίου θεωρήματος του Fermat.

Η βασική ερώτηση είναι αν:

$\displaystyle{r_a = r_{a+1} = a+1 \implies v(a+1) = v(a) + 1}$

Λέξεις Κλειδιά:

Θεωρία-Στοιχειωδών-Αριθμών

Απάντηση

1 δημοσίευση • Σελίδα 1 από 1

Επιστροφή σε “ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ”

Μέλη σε σύνδεση

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης