Να τα πάρουμε από το τέλος προς την αρχή.
Αρχικά, αν πάρουμε, για παράδειγμα, την πρωτοβάθμια θεωρία των πραγματικών αριθμών - δηλαδή, όλα τα "θεωρήματα" που αποδεικνύονται από τα αξιώματα των πραγματικών αριθμών (πλην αυτό της πληρότητας) - τότε έχουμε τουλάχιστον δύο μοντέλα που τα ικανοποιούν:
1. Το συμβατικό μοντέλο των πραγματικών αριθμών.
2. Το μη συμβατικό μοντέλο των πραγματικών αριθμών.
Μιας και το δεύτερο δεν ικανοποιεί το αξίωμα της πληρότητας, ενώ το πρώτο το ικανοποιεί (γραμμένο, προφανώς, σε δευτεροβάθμια γλώσσα), συμπεραίνουμε ότι δε γίνεται το αξίωμα της πληρότητας να περιγραφεί σε πρωτοβάθμια γλώσσα.
Άρα, πράγματι, η πρωτοβάθμια λογική δεν μπορεί να περιγράψει όλα όσα θέλουμε, ωστόσο είναι ημι-αποφασίσιμη - δηλαδή, υπάρχει αλγόριθμος ο οποίος, δεδομένου ενός θεωρήματος μπορεί, αν αυτό αποδεικνύεται από τα αξιώματά μας, να τερματίσει αποφαινόμενος ότι αποδεικνύεται, αλλά, αν αυτό δεν αποδεικνύετε, ενδέχεται να μην τερματίσει ποτέ. Για τη δευτεροβάθμια λογική δεν ισχύει κάτι τέτοιο.
Πίσω στα μοντέλα, το θεώρημα αξιοπιστίας-πληρότητας της πρωτοβάθμιας λογικής μας λέει ότι «κάθε συνεπές σύνολο τύπων είναι ικανοποιήσιμο και αντίστροφα». Δηλαδή, για κάθε σύνολο τύπων, υπάρχει δομή και απονομή (δηλ., ένα σύνολο στοιχείων και μία αντιστοίχιση των μεταβλητών με τα στοιχεία του συνόλου αυτού) που να το ικανοποιεί (να κάνει αληθείς όλες τις προτάσεις του) ανν μπορούμε να αποδείξουμε μόνο έναν εκ των

και

.
Άλλο ένα χρήσιμο θεώρημα είναι το θεώρημα της συμπάγειας («πόρισμα» του θεωρήματος αξιοπιστίας-πληρότητας), το οποίο μας λέει ότι: «Ένα σύνολο τύπων είναι ικανοποιήσιμο ανν κάθε πεπερασμένο υποσύνολό του είναι ικανοποιήσιμο». Πρακτικά, αυτό σημαίνει για να εξετάσουμε αν ένα σύνολο τύπων είναι ικανοποιήσιμο - αν υπάρχει δομή και απονομή με τα οποία να αληθεύουν όλοι οι τύποι του - αρκεί να εξετάσουμε όλα τα πεπερασμένα υποσύνολά του. (Αυτό μας θυμίζει λίγο την ιδιότητα της πεπερασμένης τομής των συμπαγών συνόλων σε τοπολογικούς χώρους και, πράγματι, σχετίζεται με αυτήν, αλλά αυτό πάει μακριά).
Λίγο χαλαρά τώρα, ας δούμε πώς «φτιάχνουμε» ένα μη συμβατικό μοντέλο αριθμητικής από το συνηθισμένο. Έστω το μοντέλο

της πρωτοβάθμιας θεωρίας των φυσικών αριθμών (με διάταξη, διάδοχο και 0, ας πούμε). Θα συμβολίζουμε αυτή τη θεωρία με

. Θεωρούμε τους τύπους (για τους πιο λεπτομερείς, φροντίζουμε η

να μην έχει ελεύθερες εμφανίσεις στην

):
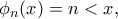
όπου με

συμβολίζουμε τον

οστό διάδοχο του μηδενός (τον

ως φυσικό αριθμό, δηλαδή). Έστω επίσης

το σύνολο όλων αυτών των τύπων. Τώρα, αν

είναι ένα πεπερασμένο υποσύνολο της

, τότε θα υπάρχει

τέτοιο ώστε:

Τότε, με μοντέλο τους συνήθεις φυσικούς αριθμούς και απονέμοντας στην

την τιμή

είναι σαφές ότι το

ικανοποιείται, άρα και το

ικανοποιείται.
Από το θεώρημα της Συμπάγειας, λοιπόν, το

ικανοποιείται. Επομένως, υπάρχει δομή

και απονομή

έτσι ώστε όλοι οι τύποι του

να ικανοποιούνται. Υπάρχει, δηλαδή, στοιχείο

τέτοιο ώστε:

για όλα τα

- τους συνήθεις φυσικούς αριθμούς.
Εμφανώς, η συνήθης θεωρία των φυσικών περιέχεται σε αυτήν του νέου μοντέλου μας - ας την ονομάσουμε

. Ωστόσο, ισχύει και το αντίστροφο. Πράγματι, αν, προς άτοπο, υπήρχε

, τότε, από την συνέπεια της

- θεώρημα αξιοπιστίας πληρότητας, αφού η

είναι ικανοποιήσιμη - θα έπρεπε

, άτοπο, γιατί

, αφού και η

είναι συνεπής - αφού είναι ικανοποιήσιμη.
Άρα,
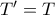
, οπότε τα δύο μοντέλα έχουν την ίδια θεωρία.
Από το παραπάνω προκύπτει εύκολα - αφού στο σύνηθες μοντέλο έχουμε την πρόταση ότι «το μοντέλο δεν είναι άνω φραγμένο» ότι υπάρχει ακολουθία «νέων» - «μη συμβατικών» - στοιχείων
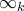
τέτοια ώστε:

δηλαδή, υπάρχουν άπειροι «μη φραγμένοι» φυσικοί αριθμοί.
Γενικά, για τη σχέση συμβατικών και μη συμβατικών μοντέλων μίας θεωρίας είναι σημαντικό το
Transfer Principle.
 .
. πρέπει να αξιωματικοποιούνται κάπως. Αν δεν γίνεται αυτό, τότε πάει να πει ότι η λογική πρώτου βαθμού δεν μπορεί να στηρίξει όλα τα μαθηματικά.
πρέπει να αξιωματικοποιούνται κάπως. Αν δεν γίνεται αυτό, τότε πάει να πει ότι η λογική πρώτου βαθμού δεν μπορεί να στηρίξει όλα τα μαθηματικά.
 και
και  .
. της πρωτοβάθμιας θεωρίας των φυσικών αριθμών (με διάταξη, διάδοχο και 0, ας πούμε). Θα συμβολίζουμε αυτή τη θεωρία με
της πρωτοβάθμιας θεωρίας των φυσικών αριθμών (με διάταξη, διάδοχο και 0, ας πούμε). Θα συμβολίζουμε αυτή τη θεωρία με  . Θεωρούμε τους τύπους (για τους πιο λεπτομερείς, φροντίζουμε η
. Θεωρούμε τους τύπους (για τους πιο λεπτομερείς, φροντίζουμε η  να μην έχει ελεύθερες εμφανίσεις στην
να μην έχει ελεύθερες εμφανίσεις στην 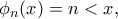
 συμβολίζουμε τον
συμβολίζουμε τον  οστό διάδοχο του μηδενός (τον
οστό διάδοχο του μηδενός (τον  το σύνολο όλων αυτών των τύπων. Τώρα, αν
το σύνολο όλων αυτών των τύπων. Τώρα, αν  είναι ένα πεπερασμένο υποσύνολο της
είναι ένα πεπερασμένο υποσύνολο της  , τότε θα υπάρχει
, τότε θα υπάρχει  τέτοιο ώστε:
τέτοιο ώστε:
 είναι σαφές ότι το
είναι σαφές ότι το  ικανοποιείται, άρα και το
ικανοποιείται, άρα και το  και απονομή
και απονομή  έτσι ώστε όλοι οι τύποι του
έτσι ώστε όλοι οι τύποι του  να ικανοποιούνται. Υπάρχει, δηλαδή, στοιχείο
να ικανοποιούνται. Υπάρχει, δηλαδή, στοιχείο  τέτοιο ώστε:
τέτοιο ώστε:
 - τους συνήθεις φυσικούς αριθμούς.
- τους συνήθεις φυσικούς αριθμούς. . Ωστόσο, ισχύει και το αντίστροφο. Πράγματι, αν, προς άτοπο, υπήρχε
. Ωστόσο, ισχύει και το αντίστροφο. Πράγματι, αν, προς άτοπο, υπήρχε  , τότε, από την συνέπεια της
, τότε, από την συνέπεια της  , άτοπο, γιατί
, άτοπο, γιατί  , αφού και η
, αφού και η 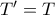 , οπότε τα δύο μοντέλα έχουν την ίδια θεωρία.
, οπότε τα δύο μοντέλα έχουν την ίδια θεωρία.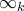 τέτοια ώστε:
τέτοια ώστε:

 ).
). ).
). ) για κάθε
) για κάθε  .
. ) για κάθε
) για κάθε  με πεδίο αναφοράς το σύνολο των συμβόλων μεταβλητών (δηλαδή, δεν μπορείς να ποσοδείξεις ένα κατηγόρημα ή μία σταθερά ή ένα σύμβολο συνάρτησης). Officially, μόνο ο ένας ποσοσδείκτης μας αρκεί.
με πεδίο αναφοράς το σύνολο των συμβόλων μεταβλητών (δηλαδή, δεν μπορείς να ποσοδείξεις ένα κατηγόρημα ή μία σταθερά ή ένα σύμβολο συνάρτησης). Officially, μόνο ο ένας ποσοσδείκτης μας αρκεί. με τα όλα του, χωρίς το αξίωμα της πληρότητας - δεν περιγράφεται σε πρωτοβάθμια γλώσσα - και το μη συμβατικό μοντέλο
με τα όλα του, χωρίς το αξίωμα της πληρότητας - δεν περιγράφεται σε πρωτοβάθμια γλώσσα - και το μη συμβατικό μοντέλο  των πραγματικών παρέα με τα απειροστά - hyperreals, όπως τους λένε. Αυτά έχουν ακριβώς την ίδια θεωρία, δηλαδή, ότι αποδεικνύεται στο ένα, αποδεικνύεται και στο άλλο και αντίστροφα. Επομένως, αν πάρουμε το Θ.Μ.Ε.Τ., που θέλει αξίωμα πληρότητας, αφού δεν ισχύει στο
των πραγματικών παρέα με τα απειροστά - hyperreals, όπως τους λένε. Αυτά έχουν ακριβώς την ίδια θεωρία, δηλαδή, ότι αποδεικνύεται στο ένα, αποδεικνύεται και στο άλλο και αντίστροφα. Επομένως, αν πάρουμε το Θ.Μ.Ε.Τ., που θέλει αξίωμα πληρότητας, αφού δεν ισχύει στο ![f:[a,b]\to\mathbb{R} f:[a,b]\to\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/4ce30d48dad9c70392ca8d3c52ee79fe.png) συνεχής με
συνεχής με ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) διάστημα του
διάστημα του  παίρνει μέγιστη και ελάχιστη τιμή.
παίρνει μέγιστη και ελάχιστη τιμή. ορισμούς του Weierstrass ως προς την αλήθεια της.
ορισμούς του Weierstrass ως προς την αλήθεια της. δεν αποδεικνύει την πρόταση
δεν αποδεικνύει την πρόταση  αν η
αν η