Νομίζω ότι κανείς δεν μπορει να αμφισβητήσει ότι το

με

και

είναι μοντέλο του

.
Αντί για το

και το

βάλτε όποια σύμβολα θέλετε, δεν έχει σημασία.
Άρα αφού το

έχει μοντέλο τότε το

είναι συνεπές(Θεώρημα Godel).
Το θέμα είναι ότι όλες οι αποδείξεις συνέπειας είναι σχετικές. Δηλαδή ότι

είναι συνεπές τότε και το

είναι συνεπές.
Δεν έχω ξαναδεί πουθενά απόλυτη απόδειξη συνέπειας. Ποιά είναι η γνώμη σας; Είναι η παραπάνω απόλυτη απόδειξη συνέπειας;
Ένας θα μπορούσε να πει ότι οι απόλυτες αποδείξεις συνέπειας δεν υπάρχουν, γιατί για να χτίσεις ένα μοντέλο για ένα σύστημα

πρέπει να ξεκινήσεις από κάπου αλλού(δεν μπορείς να χτίσεις μοντέλο από το πουθενά).
Με άλλες λέξεις μπορεί να μου πει κάποιος τι ε'ιναι το

και το

που γράφεις; Δεν πρέπει να τα ορίσουμε πρώτα;
Από μια άποψη έχει δίκιο. Είναι δηλαδή κάπως θέμα οπτικής γωνίας.
Αν το δούμε από κάποια(πιο σωστή) οπτική γωνία μπορούμε να πούμε ότι το συγκεκεριμένο σύνολο(

) σίγουρα
υπάρχει στον κόσμο της αντίληψής μας και κανείς να αμφισβητήσει ότι το

μαζί με την συνθήκη

είναι κάτι που υπάρχει. Δεν είναι σαν το σύνολο όλων των συνόλων που είναι περίεργο αντικείμενο αφου έχει την ιδιότητα ότι ανήκει στον εαυτό του.
Καλός είναι ο φορμαλισμός αλλά είναι καλύτερα να έχουμε τα μάτια μας ανοιχτά.
Περιμένω τη γνώμη σας πάνω σε αυτό τι θέμα(όχι αναγκαστικά για το

) αλλά γενικά στο θέμα που θίγεται.
 και ορίσουμε την σχέση
και ορίσουμε την σχέση  με
με  ,
, ,
, ικανοποιεί τα 7 από τα 9 αξιώματα της ZFC.
ικανοποιεί τα 7 από τα 9 αξιώματα της ZFC. .
. ικανοποιεί το αξίωμα του απείρου.
ικανοποιεί το αξίωμα του απείρου.
 για κάθε
για κάθε  .
. δεν ανήκει στο V αφού δεν είναι ούτε το
δεν ανήκει στο V αφού δεν είναι ούτε το  ούτε το
ούτε το  .
.  δίνει ύπαρξη συνόλου που περιέχει τα
δίνει ύπαρξη συνόλου που περιέχει τα  . Εδώ ισχύει αυτό το πιο ασθενές Axiom of Pairing. Σίγουρα όμως δεν ισχύει το Axiom of Specification/Separation. Το συγκεκριμένο δίνει ύπαρξη συνόλου
. Εδώ ισχύει αυτό το πιο ασθενές Axiom of Pairing. Σίγουρα όμως δεν ισχύει το Axiom of Specification/Separation. Το συγκεκριμένο δίνει ύπαρξη συνόλου  . Τέτοιο σύνολο όμως πάλι δεν υπάρχει στο
. Τέτοιο σύνολο όμως πάλι δεν υπάρχει στο  . Μάλλον για να πάρεις ότι αν ισχύει το axiom of foundation συνεπάγεται ότι
. Μάλλον για να πάρεις ότι αν ισχύει το axiom of foundation συνεπάγεται ότι  έχουμε ότι αν
έχουμε ότι αν  τότε υπάρχει
τότε υπάρχει  ώστε
ώστε  .
. τότε αναγκαστικά
τότε αναγκαστικά  . Αν πάρεις
. Αν πάρεις  τότε
τότε  .
. είναι συνεπής;
είναι συνεπής; θα είναι συνεπής;
θα είναι συνεπής; . Επειδή
. Επειδή  τότε υπάρχει
τότε υπάρχει  ώστε
ώστε  . Όμως
. Όμως  . Άρα
. Άρα  ή ισοδύναμα
ή ισοδύναμα  και
και  .
. έχει μοντέλο τότε το
έχει μοντέλο τότε το  είναι συνεπές.
είναι συνεπές. ) σίγουρα
) σίγουρα  , δηλαδή το
, δηλαδή το  ερμηνεύεται ως την παραπάνω διμελή σχέση η οποία δε βλέπω γιατί πρέπει να έχει κατ' ανάγκη μία «κοινή αντιληπτική ερμηνεία».
ερμηνεύεται ως την παραπάνω διμελή σχέση η οποία δε βλέπω γιατί πρέπει να έχει κατ' ανάγκη μία «κοινή αντιληπτική ερμηνεία».
 είναι κάτι που υπάρχει;
είναι κάτι που υπάρχει; με την τελευταία έννοια που αναφέρεις - δηλαδή, αν υπάρχει «μοντέλο» - σε μία πρωτοβάθμια γλώσσα υποθέτουμε a priori ότι το σύμπαν της δομής είναι μη κενό, επομένως, ασφαλώς, κάτι θα υπάρχει εκεί μέσα. Όμως, υπάρχει διότι το υποθέτουμε ότι υπάρχει.
με την τελευταία έννοια που αναφέρεις - δηλαδή, αν υπάρχει «μοντέλο» - σε μία πρωτοβάθμια γλώσσα υποθέτουμε a priori ότι το σύμπαν της δομής είναι μη κενό, επομένως, ασφαλώς, κάτι θα υπάρχει εκεί μέσα. Όμως, υπάρχει διότι το υποθέτουμε ότι υπάρχει.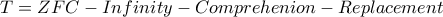 είναι συνεπής τότε και η
είναι συνεπής τότε και η  είναι συνεπή παρά να πιστέψεις ότι η
είναι συνεπή παρά να πιστέψεις ότι η