
ΕΩΣ 1/1
Συντονιστής: polysot
 και
και  η εξίσωση γίνεται:
η εξίσωση γίνεται: ή αλλιώς
ή αλλιώς 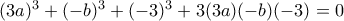 που είναι η ταυτότητα του Euler. Άρα πρέπει είτε
που είναι η ταυτότητα του Euler. Άρα πρέπει είτε 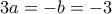 που δεν οδηγεί σε λύσεις είτε
που δεν οδηγεί σε λύσεις είτε  .
.  έχει
έχει 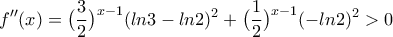 άρα η
άρα η  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.  παίρνουμε
παίρνουμε 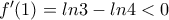 και
και  άρα από Bolzano η
άρα από Bolzano η  έχει μία ακριβώς (επειδή είναι γνησίως αύξουσα) ρίζα στο
έχει μία ακριβώς (επειδή είναι γνησίως αύξουσα) ρίζα στο  , έστω
, έστω  .
. 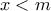 είναι
είναι 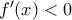 και άρα η
και άρα η  εκεί είναι γνησίως φθίνουσα ενώ για
εκεί είναι γνησίως φθίνουσα ενώ για 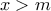 είναι
είναι  άρα η
άρα η  εκεί είναι γνησίως αύξουσα. Επειδή
εκεί είναι γνησίως αύξουσα. Επειδή 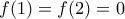 , οι
, οι  και
και  είναι οι μοναδικές ρίζες της
είναι οι μοναδικές ρίζες της  και άρα της εξίσωσής μας.
και άρα της εξίσωσής μας.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες