Πρόβλημα 1
Αν οι
 είναι θετικοί πραγματικοί αριθμοί με άθροισμα
είναι θετικοί πραγματικοί αριθμοί με άθροισμα  να αποδείξετε την ανισότητα:
να αποδείξετε την ανισότητα:
Πότε ισχύει η ισότητα;
Πρόβλημα 2
Δίνεται ορθογώνιο τρίγωνο
 στο
στο  , το έκκεντρο του
, το έκκεντρο του  και το ύψος
και το ύψος  . Ο κύκλος
. Ο κύκλος 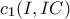 τέμνει τις
τέμνει τις 
στα σημεία
 αντιστοίχως. Αν
αντιστοίχως. Αν 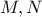 είναι τα έκκεντρα των τριγώνων
είναι τα έκκεντρα των τριγώνων  και
και  αντιστοίχως να αποδείξετε ότι
αντιστοίχως να αποδείξετε ότιη
 είναι παράλληλη της
είναι παράλληλη της  .
.Πρόβλημα 3
Να βρεθεί η ελάχιστη δυνατή τιμή του θετικού ακέραιου
 έτσι ώστε ο αριθμός:
έτσι ώστε ο αριθμός: να είναι ακέραιος για κάθε θετικό ακέραιο
να είναι ακέραιος για κάθε θετικό ακέραιο  .
.Πρόβλημα 4
Δίνεται το σύνολο
 . Ένα υποσύνολο του
. Ένα υποσύνολο του  (έστω
(έστω  με
με  )
)θα ονομάζεται "προοπτικό" εάν:
(1)
 .
.(2)
 .
.Να βρεθεί η ελάχιστη δυνατή τιμή του
 έτσι ώστε να υπάρχει "προοπτικό" υποσύνολο του
έτσι ώστε να υπάρχει "προοπτικό" υποσύνολο του  με
με  στοιχεία αλλά
στοιχεία αλλάκάθε υποσύνολο του
 με
με  στοιχεία να μην είναι "προοπτικό".
στοιχεία να μην είναι "προοπτικό".Η γεωμετρία δεν είναι δική μου.

 , οπότε
, οπότε 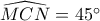 (1).
(1).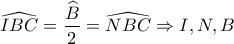 συνευθειακά.
συνευθειακά. , οπότε
, οπότε  (2).
(2).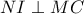 , και όμοια
, και όμοια  , οπότε
, οπότε  , συνεπώς
, συνεπώς  (3).
(3). (4).
(4). .
. παίρνουμε
παίρνουμε  και
και  .
.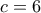 παίρνουμε
παίρνουμε  και
και  .
.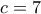 ο
ο  είναι πάντοτε ακέραιος, και θα έχουμε τελειώσει.
είναι πάντοτε ακέραιος, και θα έχουμε τελειώσει.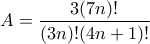 .
. .
. (1).
(1).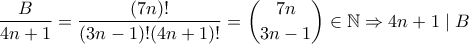 (2).
(2). είναι
είναι  .
. (3).
(3). .
. .
.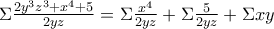


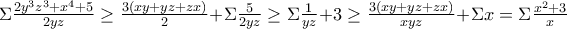


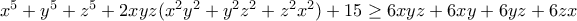




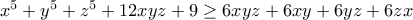

 , άρα
, άρα 



 έχουμε πως
έχουμε πως 

 έχουμε πως
έχουμε πως 
 που ισχύει.
που ισχύει.

 .
.
 (Schur).
(Schur).
 καταφέρνουμε να ομογενοποιήσουμε τους όρους.
καταφέρνουμε να ομογενοποιήσουμε τους όρους.


 τον Μ.Κ.Δ. και με
τον Μ.Κ.Δ. και με  το Ε.Κ.Π.)
το Ε.Κ.Π.)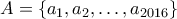 ένα προοπτικό υποσύνολο του
ένα προοπτικό υποσύνολο του  .
. , έστω
, έστω  η μεγαλύτερη δύναμη που διαιρεί τον
η μεγαλύτερη δύναμη που διαιρεί τον  , δηλαδή
, δηλαδή  , με
, με  .
.  , ή
, ή  .
.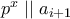 η μεγαλύτερη δύναμη του
η μεγαλύτερη δύναμη του  και όμοια ορίζουμε
και όμοια ορίζουμε  .
. ή
ή  , το Λήμμα αποδείχτηκε. Έστω λοιπόν
, το Λήμμα αποδείχτηκε. Έστω λοιπόν 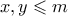 .
. , και αφού
, και αφού  .
. .
.
 , και αφού
, και αφού  .
. και
και  , με
, με  .
.


 .
. , έχουμε ότι
, έχουμε ότι 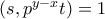 , αφού και
, αφού και  .
.  .
. , έχουμε άτοπο, αφού
, έχουμε άτοπο, αφού  . Πρέπει λοιπόν
. Πρέπει λοιπόν 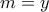 . Άρα,
. Άρα,  .
. , και
, και  ,
,  .
.
 , αφού
, αφού  , που για
, που για  , είναι άτοπο. Άρα, πάλι
, είναι άτοπο. Άρα, πάλι  , και αφού
, και αφού  , είναι
, είναι  .
.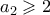 , άρα
, άρα  , και άρα
, και άρα  , δηλαδή
, δηλαδή  .
. υπάρχει ένα προοπτικό σύνολο
υπάρχει ένα προοπτικό σύνολο  , με
, με  και
και  , για κάθε
, για κάθε  .
. .
. ως εξής:
ως εξής: .
. , τότε από την 2η σχέση πρέπει
, τότε από την 2η σχέση πρέπει  ή
ή  .
. συνεπώς
συνεπώς  +
+