Ολοκληρώσιμη συνάρτηση

#1

Έστω $f:[0,1] \to \mathbb{R}$ μία συνάρτηση, ώστε για κάθε $\varepsilon >0$ το σύνολο $A_{\varepsilon}=\{t \in [0,1]/|f(t)| \geq \varepsilon \}$ είναι πεπερασμένο. Να αποδειχθεί ότι η

είναι ολοκληρώσιμη και $\int_0^1f=0$
(Νεγρεπόντης-Γιωτόπουλος-Γιαννακούλιας, Απειροστικός Ι,14-24)

#2

s.kap έγραψε:Έστω $f:[0,1] \to \mathbb{R}$ μία συνάρτηση, ώστε για κάθε $\varepsilon >0$ το σύνολο $A_{\varepsilon}=\{t \in [0,1]/|f(t)| \geq \varepsilon \}$ είναι πεπερασμένο. Να αποδειχθεί ότι η είναι ολοκληρώσιμη και $\int_0^1f=0$
(Νεγρεπόντης-Γιωτόπουλος-Γιαννακούλιας, Απειροστικός Ι,14-24)

Με κριτήριο Riemann, έστω ε >0. Από την υπόθεση υπάρχουν πεπερασμένα το πλήθος x_1, ... , x_k

με
$|f(x_k)| \ge \epsilon/2$ . Για τα υπόλοιπα x είναι φυσικά |f(x)| < ε/2. Ορίζουμε διαστήματα I_k

με κέντρα

τόσο μικρά ώστε το
συνολικό άθροισμα των |f(x_k)||I_k|

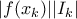να είναι < ε/2. Τώρα το άνω άθροισμα Rieman είναι < (μήκος [0,1])ε/2 + ε/2 = ε. Όμοια το
κάτω άθροισμα > -ε. Συνεπώς η διαφορά τους είναι < 2ε και άρα η συνάρτηση ολοκληρώνεται. Επίσης, το ολοκλήρωμα είναι 0 γιατί
ο 0 είναι ο μοναδικός αριθμός ανάμεσα σε όλα τα -ε και ε.

Άλλος τρόπος να βρούμε την τιμή του ολοκληρώματος (ακατάλληλος για Απειροστικό Ι, αλλά με χρήση τεχνικών από το
ολοκλήρωμα Lebesgue): H υπόθεση δίνει ότι το σύνολο των χ με $f(x) \ne 0 = \cup _n \{ x \in [0,1] / |f(x)| \ge 1/n \}$ = αριθμήσιμη
ένωση πεπερασμένων = αριθμήσιμο, και λοιπά.

Φιλικά,

Μιχάλης

#3

Μιχάλη, έπιασες και τους δύο τρόπους, οπότε εγώ τι να πω;
Φιλικά

Ολοκληρώσιμη συνάρτηση

Ολοκληρώσιμη συνάρτηση

Re: Ολοκληρώσιμη συνάρτηση

Re: Ολοκληρώσιμη συνάρτηση

Μέλη σε σύνδεση