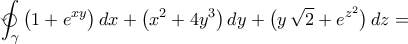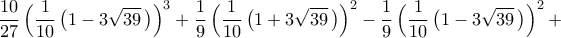Λύση: 
είναι το στερεό που ορίζουν τα παραβολοειδή

και
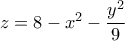
,

είναι η επιφάνειά του και
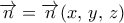
είναι το μοναδιαίο διάνυσμα, το ορθογώνιο προς την

στο σημείο

και με φορά προς το εσωτερικό της

.
Η τομή των δύο παραβολοειδών είναι η έλλειψη

που βρίσκεται στο επίπεδο

, αφού ισχύουν

.

- volume.png (100.06 KiB) Προβλήθηκε 625 φορές
α. Άν

το στερεό που ορίζει το παραβολοειδές

και το επίπεδο

και

το στερεό που ορίζει το παραβολοειδές

και το επίπεδο

, τότε

.
Επειδή τα παραβολοειδή είναι συμμετρικά, ώς πρός το επίπεδο

, για την εύρεση του όγκου
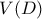
αρκεί να βρεθεί ο όγκος

.

![\displaystyle\int_{0}^{2\pi}\int_{0}^{1}{4\,({1-\rho^2})\,12\rho\,d\rho\,d\theta}=12\int_{0}^{2\pi}{\bigl[{2\rho^2-\rho^4}\bigr]_{0}^{1}\,d\theta}=12\int_{0}^{2\pi}{d\theta}=24\pi \displaystyle\int_{0}^{2\pi}\int_{0}^{1}{4\,({1-\rho^2})\,12\rho\,d\rho\,d\theta}=12\int_{0}^{2\pi}{\bigl[{2\rho^2-\rho^4}\bigr]_{0}^{1}\,d\theta}=12\int_{0}^{2\pi}{d\theta}=24\pi](/forum/ext/geomar/texintegr/latexrender/pictures/2e26c4e6122c0cd18806ce9d8b673415.png)
.
Άρα


Για την αλλαγή μεταβλητών

προκύπτει
 β.
β. Τό

είναι

-κανονικό,

-κανονικό και
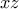
-κανονικό και η συνάρτηση
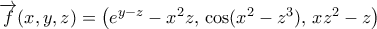
,

, είναι

στο

. Επομένως πλοιρούνται οί προυποθέσεις για το Θεώρημα Gauss.


 γ.
γ. 
.
Επειδή

, για τα σημεία του
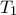
πρέπει

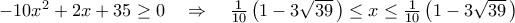
.
Επίσης πρέπει

.

.
Επειδή

, για τα σημεία του

πρέπει

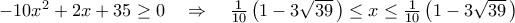
.
Επίσης πρέπει

.

- lineint.png (142.85 KiB) Προβλήθηκε 625 φορές
Η τομή του

με το επίπεδο

, είναι το χωρίο

, του

,
ενώ η τομή του

με το επίπεδο

, είναι το χωρίο

, του

.
Επομένως το χωρίο του

πού προκύπτει από την τομή του

με το

είναι το

. Η καμπύλη

είναι το σύνορο του

ενώ ένα μοναδιαίο διάνυσμα κάθετο στο

είναι το

. Αν

,

, τότε

Από το Θεώρημα Stokes προκύπτει ότι
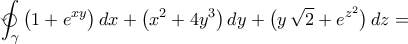



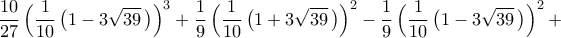


 είναι το στερεό που ορίζουν τα παραβολοειδή
είναι το στερεό που ορίζουν τα παραβολοειδή  και
και 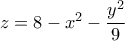 ,
,  είναι η επιφάνειά του και
είναι η επιφάνειά του και 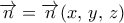 είναι το μοναδιαίο διάνυσμα, το ορθογώνιο προς την
είναι το μοναδιαίο διάνυσμα, το ορθογώνιο προς την  στο σημείο
στο σημείο  και με φορά προς το εσωτερικό της
και με φορά προς το εσωτερικό της  , να υπολογισθούν:
, να υπολογισθούν: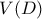 .
. , όπου
, όπου 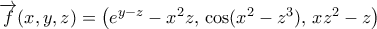 ,
,  .
. , όπου
, όπου  είναι η θετικά προσανανατολισμένη καμπύλη που προκύπτει από την τομή του επιπέδου με εξίσωση
είναι η θετικά προσανανατολισμένη καμπύλη που προκύπτει από την τομή του επιπέδου με εξίσωση  και της επιφάνειας
και της επιφάνειας  .
.

 που βρίσκεται στο επίπεδο
που βρίσκεται στο επίπεδο  , αφού ισχύουν
, αφού ισχύουν  .
.
 το στερεό που ορίζει το παραβολοειδές
το στερεό που ορίζει το παραβολοειδές  και το επίπεδο
και το επίπεδο  το στερεό που ορίζει το παραβολοειδές
το στερεό που ορίζει το παραβολοειδές  και το επίπεδο
και το επίπεδο  .
. .
.
![\displaystyle\int_{0}^{2\pi}\int_{0}^{1}{4\,({1-\rho^2})\,12\rho\,d\rho\,d\theta}=12\int_{0}^{2\pi}{\bigl[{2\rho^2-\rho^4}\bigr]_{0}^{1}\,d\theta}=12\int_{0}^{2\pi}{d\theta}=24\pi \displaystyle\int_{0}^{2\pi}\int_{0}^{1}{4\,({1-\rho^2})\,12\rho\,d\rho\,d\theta}=12\int_{0}^{2\pi}{\bigl[{2\rho^2-\rho^4}\bigr]_{0}^{1}\,d\theta}=12\int_{0}^{2\pi}{d\theta}=24\pi](/forum/ext/geomar/texintegr/latexrender/pictures/2e26c4e6122c0cd18806ce9d8b673415.png) .
. 
 Για την αλλαγή μεταβλητών
Για την αλλαγή μεταβλητών  προκύπτει
προκύπτει 
 -κανονικό,
-κανονικό,  -κανονικό και
-κανονικό και 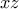 -κανονικό και η συνάρτηση
-κανονικό και η συνάρτηση  στο
στο  . Επομένως πλοιρούνται οί προυποθέσεις για το Θεώρημα Gauss.
. Επομένως πλοιρούνται οί προυποθέσεις για το Θεώρημα Gauss.


 .
.  , για τα σημεία του
, για τα σημεία του 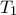 πρέπει
πρέπει 
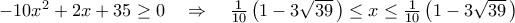 .
.  .
. .
.  πρέπει
πρέπει  .
. , είναι το χωρίο
, είναι το χωρίο  , του
, του  ,
,  , του
, του  . Η καμπύλη
. Η καμπύλη  ενώ ένα μοναδιαίο διάνυσμα κάθετο στο
ενώ ένα μοναδιαίο διάνυσμα κάθετο στο  . Αν
. Αν  ,
,