 συγκλίνει, εφαρμόζοντας τό κριτήριο πηλίκου τού D' Alembert. (
συγκλίνει, εφαρμόζοντας τό κριτήριο πηλίκου τού D' Alembert. (  = δεκαδικός λογάριθμος )
= δεκαδικός λογάριθμος )Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 συγκλίνει, εφαρμόζοντας τό κριτήριο πηλίκου τού D' Alembert. (
συγκλίνει, εφαρμόζοντας τό κριτήριο πηλίκου τού D' Alembert. (  = δεκαδικός λογάριθμος )
= δεκαδικός λογάριθμος )
 ,έχουμε
,έχουμε ![\displaystyle\frac{{\frac{{\left( {\log (n + 1)} \right)^2 }}{{\left( {\log 2} \right)^{n + 1} }}}}{{\frac{{\left( {\log n} \right)^2 }}{{\left( {\log 2} \right)^n }}}} = \frac{1}{{\log 2}}\left[ {\frac{{\log (n + 1)}}{{\log n}}} \right]^2 \displaystyle\frac{{\frac{{\left( {\log (n + 1)} \right)^2 }}{{\left( {\log 2} \right)^{n + 1} }}}}{{\frac{{\left( {\log n} \right)^2 }}{{\left( {\log 2} \right)^n }}}} = \frac{1}{{\log 2}}\left[ {\frac{{\log (n + 1)}}{{\log n}}} \right]^2](/forum/ext/geomar/texintegr/latexrender/pictures/4f0c099d7a149c87dc4a7306daa081ed.png) που τείνει στο 1/log2 για n->oo. Όμως το 1/log2>1 , αρα η σειρά απειρίζεται θετικά...
που τείνει στο 1/log2 για n->oo. Όμως το 1/log2>1 , αρα η σειρά απειρίζεται θετικά...Το πηλίκο διαδοχικών όρων είναιgrigkost έγραψε:Νά εξετασθεί άν η σειράσυγκλίνει, εφαρμόζοντας τό κριτήριο πηλίκου τού D' Alembert. (
= δεκαδικός λογάριθμος )
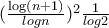 .
. , οπότε η σειρά αποκλίνει.
, οπότε η σειρά αποκλίνει. τείνουν στο άπειρο. Άρα η σειρά αποκλίνει "γρήγορα".
τείνουν στο άπειρο. Άρα η σειρά αποκλίνει "γρήγορα".Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες