
Σύγκλιση Σειράς
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
-
ttheodoros
- Δημοσιεύσεις: 83
- Εγγραφή: Κυρ Νοέμ 21, 2010 4:28 pm
- Τοποθεσία: Λευκωσία - Κύπρος
- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Σύγκλιση Σειράς
Η ακολουθία  ,
,  , των μερικών αθροισμάτων της ακολουθίας
, των μερικών αθροισμάτων της ακολουθίας  είναι φραγμένη(*) και επειδή η ακολουθία
είναι φραγμένη(*) και επειδή η ακολουθία  είναι φθίνουσα και μηδενική η σειρά
είναι φθίνουσα και μηδενική η σειρά  συγκλίνει.
συγκλίνει.
(*) Μένει να αποδειχθεί.
 ,
,  , των μερικών αθροισμάτων της ακολουθίας
, των μερικών αθροισμάτων της ακολουθίας  είναι φραγμένη(*) και επειδή η ακολουθία
είναι φραγμένη(*) και επειδή η ακολουθία  είναι φθίνουσα και μηδενική η σειρά
είναι φθίνουσα και μηδενική η σειρά  συγκλίνει.
συγκλίνει.(*) Μένει να αποδειχθεί.

-
ttheodoros
- Δημοσιεύσεις: 83
- Εγγραφή: Κυρ Νοέμ 21, 2010 4:28 pm
- Τοποθεσία: Λευκωσία - Κύπρος
- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Σύγκλιση Σειράς
Θεόδωρεttheodoros έγραψε:Συγκλίνει ομοιόμορφα?
δεν είναι σειρά συναρτήσεων για να εξετάσουμε ομοιόμορφη σύγκλιση.
Μήπως εννοείς απόλυτα ;
Υ.Γ. Όσο για την σύγκλιση, το δύσκολο κομμάτι(*) το "παρέκαμψα" αλλά είναι, όντος, δύσκολο κομμάτι!
Ίσως δοθεί μια διαφορετική απόδειξη από κάποιον άλλον.

-
caley-hamilton
- Δημοσιεύσεις: 84
- Εγγραφή: Κυρ Φεβ 20, 2011 1:05 am
Re: Σύγκλιση Σειράς
Εδώ χρησιμοποιήσατε το κριτήριο Dirichlet,έτσι δεν είναι?grigkost έγραψε:Η ακολουθία,
, των μερικών αθροισμάτων της ακολουθίας
είναι φραγμένη(*) και επειδή η ακολουθία
είναι φθίνουσα και μηδενική η σειρά
συγκλίνει.
(*) Μένει να αποδειχθεί.
Εάν επρόκειτο να ξυπνήσω έπειτα από έναν ύπνο χιλίων ετών,
η πρώτη μου ερώτηση θα ήταν:Αποδείχθηκε η υπόθεση Riemann;
David Hilber (1862-1943)
η πρώτη μου ερώτηση θα ήταν:Αποδείχθηκε η υπόθεση Riemann;
David Hilber (1862-1943)
- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Σύγκλιση Σειράς
Ναι. Παράλειψή μου, αλλά είναι γνωστό κριτήριο.caley-hamilton έγραψε:Εδώ χρησιμοποιήσατε το κριτήριο Dirichlet,έτσι δεν είναι?grigkost έγραψε:Η ακολουθία,
, των μερικών αθροισμάτων της ακολουθίας
είναι φραγμένη(*) και επειδή η ακολουθία
είναι φθίνουσα και μηδενική η σειρά
συγκλίνει.
(*) Μένει να αποδειχθεί.

- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Σύγκλιση Σειράς
Κάποιες σκέψεις: Ισχυρίζομαι ότι 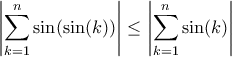 .
.
Αν ισχύει ο ισχυρισμός, τότε επειδή
 τελειώσαμε.
τελειώσαμε.
Μελετώντας την παρατηρούμε ότι
παρατηρούμε ότι
 στα διαστήματα
στα διαστήματα ![[2k\pi,(2k+1)\pi] [2k\pi,(2k+1)\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/096b2ffb0343e97cfeb7885e0027097f.png) όπου
όπου  είναι
είναι 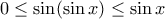 με τις ισότητες να ισχύουν μόνο στα άκρα και αντίστοιχα
με τις ισότητες να ισχύουν μόνο στα άκρα και αντίστοιχα
 στα διαστήματα
στα διαστήματα ![\displaystyle{[(2k+1)\pi,(2k+2)\pi]} \displaystyle{[(2k+1)\pi,(2k+2)\pi]}](/forum/ext/geomar/texintegr/latexrender/pictures/fccd69bd0f7517a47f3a3d397fdb2e8f.png) όπου
όπου  είναι
είναι  με τις ισότητες να ισχύουν μόνο στα άκρα.
με τις ισότητες να ισχύουν μόνο στα άκρα.
Κάνουμε ακολούθως την εξής παρατήρηση:
Έστω δυο πεπερασμένα σύνολα πραγματικών και
και  και αντίστοιχες διαμερίσεις τους
και αντίστοιχες διαμερίσεις τους  και
και  σε μη αρνητικά και αρνητικά στοιχεία αντίστοιχα όπου
σε μη αρνητικά και αρνητικά στοιχεία αντίστοιχα όπου  και
και 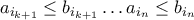 .
.
Τότε ισχύει .
.
Από τις και
και  προκύπτει ότι τα σύνολα
προκύπτει ότι τα σύνολα  και
και  έχουν τις παραπάνω ιδιότητες κάτι που αποδεικνύει τον αρχικό ισχυρισμό.
έχουν τις παραπάνω ιδιότητες κάτι που αποδεικνύει τον αρχικό ισχυρισμό.
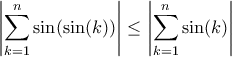 .
.Αν ισχύει ο ισχυρισμός, τότε επειδή
 τελειώσαμε.
τελειώσαμε.Μελετώντας την
 παρατηρούμε ότι
παρατηρούμε ότι  στα διαστήματα
στα διαστήματα ![[2k\pi,(2k+1)\pi] [2k\pi,(2k+1)\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/096b2ffb0343e97cfeb7885e0027097f.png) όπου
όπου  είναι
είναι 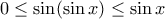 με τις ισότητες να ισχύουν μόνο στα άκρα και αντίστοιχα
με τις ισότητες να ισχύουν μόνο στα άκρα και αντίστοιχα στα διαστήματα
στα διαστήματα ![\displaystyle{[(2k+1)\pi,(2k+2)\pi]} \displaystyle{[(2k+1)\pi,(2k+2)\pi]}](/forum/ext/geomar/texintegr/latexrender/pictures/fccd69bd0f7517a47f3a3d397fdb2e8f.png) όπου
όπου  είναι
είναι  με τις ισότητες να ισχύουν μόνο στα άκρα.
με τις ισότητες να ισχύουν μόνο στα άκρα.Κάνουμε ακολούθως την εξής παρατήρηση:
Έστω δυο πεπερασμένα σύνολα πραγματικών
 και
και  και αντίστοιχες διαμερίσεις τους
και αντίστοιχες διαμερίσεις τους  και
και  σε μη αρνητικά και αρνητικά στοιχεία αντίστοιχα όπου
σε μη αρνητικά και αρνητικά στοιχεία αντίστοιχα όπου  και
και 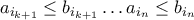 .
.Τότε ισχύει
 .
.Από τις
 και
και  προκύπτει ότι τα σύνολα
προκύπτει ότι τα σύνολα  και
και  έχουν τις παραπάνω ιδιότητες κάτι που αποδεικνύει τον αρχικό ισχυρισμό.
έχουν τις παραπάνω ιδιότητες κάτι που αποδεικνύει τον αρχικό ισχυρισμό.Εσύ....; Θα γίνεις κανίβαλος....;
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15763
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Σύγκλιση Σειράς
Αναστάση, κάτι ... δεν μου αρέσει. Οι συνθήκες που βάζεις μου φαίνεται ότι ισοδυναμούν μεΚοτρώνης Αναστάσιος έγραψε:<...>
Έστω δυο πεπερασμένα σύνολα πραγματικώνκαι
και αντίστοιχες διαμερίσεις τους
και
σε μη αρνητικά και αρνητικά στοιχεία αντίστοιχα όπου
και
.
Τότε ισχύει.
<...>
 . Αυτό όμως δεν δίνει το συμπέρασμα που γράφεις. Π.χ.
. Αυτό όμως δεν δίνει το συμπέρασμα που γράφεις. Π.χ.  . Εδώ το μερικό άθροισμα των
. Εδώ το μερικό άθροισμα των  εναλλάσεται
εναλλάσεται  αλλά των
αλλά των  είναι μη κάτω φραγμένα.
είναι μη κάτω φραγμένα. Ίσως κάνω λάθος γιατί είμαι κουρασμένος από τα τρεχάματα σήμερα, αλλά δες το.
Φιλικά,
Μιχάλης
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
-
ttheodoros
- Δημοσιεύσεις: 83
- Εγγραφή: Κυρ Νοέμ 21, 2010 4:28 pm
- Τοποθεσία: Λευκωσία - Κύπρος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες
