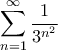 είναι ρητός ή άρρητος;
είναι ρητός ή άρρητος;Ρητός ή άρρητος;
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15763
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ρητός ή άρρητος;
Καλόόόό.s.kap έγραψε:Ο αριθμόςείναι ρητός ή άρρητος;
Αφού το μυαλό μου πήγε σε διάφορα περίεργα, να μια λύση της μιας γραμμής που δείχνει ότι ο αριθμός αυτός είναι άρρητος:
Στο τριαδικό σύστημα γραφής δεν είναι περιοδικός. Τελειώσαμε!
Άντε, και ένα ακόμη σχόλιο: Στο τριαδικό σύστημα η γραφή του αριθμού αυτού είναι
 όπου τα
όπου τα  είναι στις θέσεις
είναι στις θέσεις  . Τα διαδοχικά κενά μεταξύ τους είναι
. Τα διαδοχικά κενά μεταξύ τους είναι  , δηλαδή μεγαλώνουν. Άρα είναι με περοδικός.
, δηλαδή μεγαλώνουν. Άρα είναι με περοδικός. Φιλικά,
Μιχάλης
Re: Ρητός ή άρρητος;
Μιχάλη, καλησπέρα.
Αυτό είχα και εγώ υπόψη μου. Είναι μία πολύ έξυπνη άσκηση των Ρουμάνων Valentin Matrosenco και Ion Savu.
Αυτό είχα και εγώ υπόψη μου. Είναι μία πολύ έξυπνη άσκηση των Ρουμάνων Valentin Matrosenco και Ion Savu.
Σπύρος Καπελλίδης
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Ρητός ή άρρητος;
Όχι είναι άρρητος. Αρχικά παρατηρούμε ότι η μεγαλύτερη δύναμη του 2 η οποία διαιρεί τοpeter έγραψε:2. Έστωγνησίως αύξουσα ακολουθία φυσικών αριθμών. Είναι ο αριθμός
ρητός;
 είναι η
είναι η  . Επομένως αν ο
. Επομένως αν ο  είναι ρητός, για κάποιο αρκετά μεγάλο
είναι ρητός, για κάποιο αρκετά μεγάλο  ο παρανομαστής του θα διαιρείται με τον αριθμό
ο παρανομαστής του θα διαιρείται με τον αριθμό  .
.Ισχυρίζομαι τώρα ότι ο αριθμός
 είναι ακέραιος για κάθε
είναι ακέραιος για κάθε  .
. Πράγματι, εύκολα μπορεί να δειχθεί ότι το
 δεν διαιρεί το
δεν διαιρεί το  και άρα η μεγαλύτερη δύναμη του 2 που διαιρεί το
και άρα η μεγαλύτερη δύναμη του 2 που διαιρεί το  είναι μεγαλύτερη ή ίση με
είναι μεγαλύτερη ή ίση με  .
. Επομένως, για
 αρκετά μεγάλο, θα έχουμε ότι ο αριθμός
αρκετά μεγάλο, θα έχουμε ότι ο αριθμός 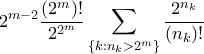 είναι ακέραιος. Αλλά
είναι ακέραιος. Αλλά 
 , άτοπο.
, άτοπο.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
