 και όσες φορές θέλουμε τα σύμβολα
και όσες φορές θέλουμε τα σύμβολα ![+,-,\cdot , : \,,\sqrt{\,},\left[\,\, \right], +,-,\cdot , : \,,\sqrt{\,},\left[\,\, \right],](/forum/ext/geomar/texintegr/latexrender/pictures/5db8832293e0171c225ee8df98240196.png) ( το σύνηθες σύμβολο του ακεραίου μέρους) καθώς επίσης δεξιές και αριστερές παρενθέσεις. Να αποδειχθεί ότι κάθε ακέραιος μπορεί να είναι η τιμή μιας τέτοιας παράστασης.
( το σύνηθες σύμβολο του ακεραίου μέρους) καθώς επίσης δεξιές και αριστερές παρενθέσεις. Να αποδειχθεί ότι κάθε ακέραιος μπορεί να είναι η τιμή μιας τέτοιας παράστασης.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 και όσες φορές θέλουμε τα σύμβολα
και όσες φορές θέλουμε τα σύμβολα ![+,-,\cdot , : \,,\sqrt{\,},\left[\,\, \right], +,-,\cdot , : \,,\sqrt{\,},\left[\,\, \right],](/forum/ext/geomar/texintegr/latexrender/pictures/5db8832293e0171c225ee8df98240196.png) ( το σύνηθες σύμβολο του ακεραίου μέρους) καθώς επίσης δεξιές και αριστερές παρενθέσεις. Να αποδειχθεί ότι κάθε ακέραιος μπορεί να είναι η τιμή μιας τέτοιας παράστασης.
( το σύνηθες σύμβολο του ακεραίου μέρους) καθώς επίσης δεξιές και αριστερές παρενθέσεις. Να αποδειχθεί ότι κάθε ακέραιος μπορεί να είναι η τιμή μιας τέτοιας παράστασης.![\displaystyle{\Bigg[\frac{4}{\sqrt{}\sqrt{}\sqrt{}...\sqrt{}4-\sqrt{}\sqrt{}...\sqrt{}4}\Bigg]} \displaystyle{\Bigg[\frac{4}{\sqrt{}\sqrt{}\sqrt{}...\sqrt{}4-\sqrt{}\sqrt{}...\sqrt{}4}\Bigg]}](/forum/ext/geomar/texintegr/latexrender/pictures/0c249b8275b3ac468872ad3f8fb07011.png) με
με  ριζικά αντίστοιχα στον παρονομαστή.
ριζικά αντίστοιχα στον παρονομαστή. τείνει στο
τείνει στο  καθώς το πλήθος των ριζικών τείνει στο άπειρο.
καθώς το πλήθος των ριζικών τείνει στο άπειρο. έχει ένα όρο σε κάθε διάστημα
έχει ένα όρο σε κάθε διάστημα 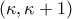 όπου
όπου  φυσικός. Το
φυσικός. Το  μπορούμε να το πάρουμε λίγο μεγαλύτερο από το
μπορούμε να το πάρουμε λίγο μεγαλύτερο από το  αν χρειαστεί γράφοντας τους αριθμούς μέχρι το
αν χρειαστεί γράφοντας τους αριθμούς μέχρι το  με άλλο τρόπο.
με άλλο τρόπο. είναι δύο μη αρνητικοί ακέραιοι τότε θεωρούμε τον αριθμό
είναι δύο μη αρνητικοί ακέραιοι τότε θεωρούμε τον αριθμό  .
.![\left[\sqrt{\sqrt{4}} \right]=1 \left[\sqrt{\sqrt{4}} \right]=1](/forum/ext/geomar/texintegr/latexrender/pictures/314368c07f345675d1e52e96177e2470.png) , κάθε
, κάθε  μπορεί να προκύψει με τρία τεσσάρια και τα επιτρεπτά σύμβολα.
μπορεί να προκύψει με τρία τεσσάρια και τα επιτρεπτά σύμβολα.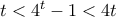 για
για ![t\in (0,1] t\in (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e32985d77fc3dabef5b39119f03eab0e.png) , προκύπτει
, προκύπτει 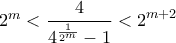 .
. .
. είναι πυκνό στο
είναι πυκνό στο  . Άρα
. Άρα ![[F(m,n)]=N [F(m,n)]=N](/forum/ext/geomar/texintegr/latexrender/pictures/e33835a4a05efd3229571d41b09edf67.png) άπειρες φορές για κάθε θετικό ακέραιο
άπειρες φορές για κάθε θετικό ακέραιο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot], MSN [Bot] και 12 επισκέπτες