Αυτό εδώ το βρήκα εντελώς τυχαία και έχει πλάκα.
Να γράψω μερικά γενικά πράγματα στην αρχή και μετά να δούμε το

.
Για κάθε φυσικό

και κάθε πραγματικό

θεωρούμε την εξίσωση

και ορίζουμε

. Κατόπιν, ορίζουμε

.
(α) Γενικά φράγματα: Ισχύει για κάθε

ότι

. Αυτά είναι και τα δυο απλά. Μιας και δεν έχει δοθεί απόδειξη για το κάτω φράγμα σκιαγραφώ μια.
Ισχυρισμός. Έστω

. Για κάθε

έχουμε

Έστω

. Τότε για κάθε ρίζα

της

έχουμε ότι

. Αν
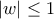
βίσκουμε ότι

. Από την τελευταία έπεται ότι

. Επομένως, για κάθε ρίζα

ισχύει

και το ζητούμενο έπεται.
(β) Υπολογισμός του

. Εδώ έχω μια λύση που διακρίνει περιπτώσεις και δεν ξέρω αν είναι πιο σύντομη απ' αυτή του Δημήτρη.
1. Όλες οι ρίζες πραγματικές.
1α. Οι ρίζες του  είναι οι
είναι οι 
: Από το Θεώρημα του Rolle έπεται ότι

και

. Σ' αυτήν την περίπτωση έχουμε
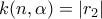
. Άρα, είναι:

ή
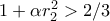
. Οπότε,

.
1β. Οι ρίζες του  είναι οι
είναι οι 
. Άρα είναι

και

, απ' όπου βρίσκουμε

και

. Επιπλέον, είναι

. Επομένως, είναι

.
2. Μια ρίζα πραγματική και δυο συζυγείς μιγαδικές. Υποθέτουμε ότι οι ρίζες είναι

. Από τους τύπους του Vieta βρίσκουμε:
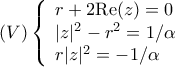
Διακρίνουμε τις περιπτώσεις:
a.

. Τότε, από τις δυο τελευταίες σχέσεις

βρίσκουμε ότι:

. Ειδικότερα,

οπότε

. Λύνοντας την τελευταία ανίσωση βρίσκουμε

.
b.

. Μπορούμε να γράψουμε

με

. Tότε, η υπόθεση δίνει

. Τότε, η δεύτερη σχέση

ξαναγράφεται

από την υπόθεση. Έπεται από την τρίτη σχέση ότι

οπότε θέτοντας

και αντικαθιστώντας στις

βρίσκουμε

. Έτσι, έχουμε:

λαμβάνοντας υπόψιν ότι

.
Συνδυάζοντας όλα τα παραπάνω προκύπτει ότι

.
Έχω μια απόδειξη που (νομίζω ότι) δίνει

. Θα την παραθέσω μόλις βρω χρόνο και την ελέγξω.
Μερικά ερωτήματα που προκύπτουν είναι τα ακόλουθα:
1. Είναι προφανές ότι
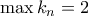
. Υπάρχει το

; Ποιο είναι το

;
2. Να βρεθεί οριακό σημείο της

.
3. (Πιο τολμηρό!) Ποια η σχέση της

με την
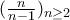
;
 ώστε η παρακάτω άσκηση να είναι σωστή:
ώστε η παρακάτω άσκηση να είναι σωστή: και
και  , να δειχθεί ότι
, να δειχθεί ότι  .
. για κάθε
για κάθε  και δεν είναι δύσκολο να ελεγχθεί ότι
και δεν είναι δύσκολο να ελεγχθεί ότι 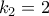 .
.  και μπορώ να δείξω ότι
και μπορώ να δείξω ότι  . (Η λύση μου είναι κάπως μακροσκελής για αυτό θα περιμένω μήπως κάποιος έχει κάποια σύντομη λύση.) Δεν έχω κάποια εικασία ακόμη για μεγαλύτερα
. (Η λύση μου είναι κάπως μακροσκελής για αυτό θα περιμένω μήπως κάποιος έχει κάποια σύντομη λύση.) Δεν έχω κάποια εικασία ακόμη για μεγαλύτερα  . Νομίζω όμως πως με χρήση μαθηματικών προγραμμάτων μπορούμε να διατυπώσουμε κάποια εικασία.
. Νομίζω όμως πως με χρήση μαθηματικών προγραμμάτων μπορούμε να διατυπώσουμε κάποια εικασία. χρησιμοποιεί παραγώγους για εύρεση ακροτάτων ορισμένων συναρτήσεων. Έβαλα την άσκηση εδώ ώστε να μην περιοριστούμε μόνο στα σχολικά εργαλεία. Έτσι κι'αλλιώς δεν γνωρίζω τι μεθόδους θα χρειαστούμε για την λύση της άσκησης.
χρησιμοποιεί παραγώγους για εύρεση ακροτάτων ορισμένων συναρτήσεων. Έβαλα την άσκηση εδώ ώστε να μην περιοριστούμε μόνο στα σχολικά εργαλεία. Έτσι κι'αλλιώς δεν γνωρίζω τι μεθόδους θα χρειαστούμε για την λύση της άσκησης.
 .
. και κάθε πραγματικό
και κάθε πραγματικό  θεωρούμε την εξίσωση
θεωρούμε την εξίσωση  και ορίζουμε
και ορίζουμε  . Κατόπιν, ορίζουμε
. Κατόπιν, ορίζουμε  .
. ότι
ότι  . Αυτά είναι και τα δυο απλά. Μιας και δεν έχει δοθεί απόδειξη για το κάτω φράγμα σκιαγραφώ μια.
. Αυτά είναι και τα δυο απλά. Μιας και δεν έχει δοθεί απόδειξη για το κάτω φράγμα σκιαγραφώ μια. έχουμε
έχουμε 
 της
της  . Αν
. Αν 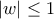 βίσκουμε ότι
βίσκουμε ότι  . Από την τελευταία έπεται ότι
. Από την τελευταία έπεται ότι  . Επομένως, για κάθε ρίζα
. Επομένως, για κάθε ρίζα  . Εδώ έχω μια λύση που διακρίνει περιπτώσεις και δεν ξέρω αν είναι πιο σύντομη απ' αυτή του Δημήτρη.
. Εδώ έχω μια λύση που διακρίνει περιπτώσεις και δεν ξέρω αν είναι πιο σύντομη απ' αυτή του Δημήτρη. είναι οι
είναι οι  : Από το Θεώρημα του Rolle έπεται ότι
: Από το Θεώρημα του Rolle έπεται ότι  και
και  . Σ' αυτήν την περίπτωση έχουμε
. Σ' αυτήν την περίπτωση έχουμε 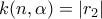 . Άρα, είναι:
. Άρα, είναι:  ή
ή 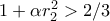 . Οπότε,
. Οπότε,  .
. είναι οι
είναι οι  . Άρα είναι
. Άρα είναι  και
και  , απ' όπου βρίσκουμε
, απ' όπου βρίσκουμε  και
και  . Επιπλέον, είναι
. Επιπλέον, είναι  . Επομένως, είναι
. Επομένως, είναι  .
. . Από τους τύπους του Vieta βρίσκουμε:
. Από τους τύπους του Vieta βρίσκουμε: 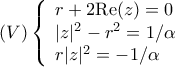
 . Τότε, από τις δυο τελευταίες σχέσεις
. Τότε, από τις δυο τελευταίες σχέσεις  βρίσκουμε ότι:
βρίσκουμε ότι:  . Ειδικότερα,
. Ειδικότερα,  οπότε
οπότε  . Λύνοντας την τελευταία ανίσωση βρίσκουμε
. Λύνοντας την τελευταία ανίσωση βρίσκουμε  .
. . Μπορούμε να γράψουμε
. Μπορούμε να γράψουμε  με
με  . Tότε, η υπόθεση δίνει
. Tότε, η υπόθεση δίνει  . Τότε, η δεύτερη σχέση
. Τότε, η δεύτερη σχέση  από την υπόθεση. Έπεται από την τρίτη σχέση ότι
από την υπόθεση. Έπεται από την τρίτη σχέση ότι  οπότε θέτοντας
οπότε θέτοντας  και αντικαθιστώντας στις
και αντικαθιστώντας στις  . Έτσι, έχουμε:
. Έτσι, έχουμε:  λαμβάνοντας υπόψιν ότι
λαμβάνοντας υπόψιν ότι  .
. . Θα την παραθέσω μόλις βρω χρόνο και την ελέγξω.
. Θα την παραθέσω μόλις βρω χρόνο και την ελέγξω.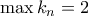 . Υπάρχει το
. Υπάρχει το  ; Ποιο είναι το
; Ποιο είναι το  ;
; .
.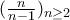 ;
; . Έστω λοιπόν το πολυώνυμο
. Έστω λοιπόν το πολυώνυμο  Αυτό έχει ρίζα το
Αυτό έχει ρίζα το  . Θα δείξω ότι όλες οι ρίζες του είναι σε απόλυτη τιμή τουλάχιστον
. Θα δείξω ότι όλες οι ρίζες του είναι σε απόλυτη τιμή τουλάχιστον  . Για αυτό αρκεί να μελετήσουμε το πολυώνυμο
. Για αυτό αρκεί να μελετήσουμε το πολυώνυμο 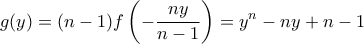 και να δείξουμε ότι όλες οι ρίζες του είναι σε απόλυτη τιμή τουλάχιστον 1.
και να δείξουμε ότι όλες οι ρίζες του είναι σε απόλυτη τιμή τουλάχιστον 1. και
και  . Για
. Για  έχουμε
έχουμε  . Επομένως από Rouché, για κάθε
. Επομένως από Rouché, για κάθε  , τα
, τα  έχουν τον ίδιο αριθμό ριζών στον κύκλο ακτίνας
έχουν τον ίδιο αριθμό ριζών στον κύκλο ακτίνας  με κέντρο το
με κέντρο το  . Επομένως το
. Επομένως το  δεν έχει ρίζα
δεν έχει ρίζα  με
με  έχει.
έχει.