----------------------------------------------------------------------------------------------------------------------
Να προσδιοριστεί το πολυώνυμο
 με
με  ,που ικανοποιεί τη συναρτησιακή σχέση:
,που ικανοποιεί τη συναρτησιακή σχέση: ,για κάθε
,για κάθε  στο
στο  ,
,όπου
 είναι συνάρτηση τέτοια,ώστε
είναι συνάρτηση τέτοια,ώστε  και
και  ,για κάθε
,για κάθε  .
.----------------------------------------------------------------------------------------------------------------------
Ευχαριστώ εκ των προτέρων.

 .
. θεωρώ την
θεωρώ την  . Αυτή ικανοποιεί τις υποθέσεις
. Αυτή ικανοποιεί τις υποθέσεις  άρα και για
άρα και για  . Aπό την
. Aπό την  .
. δίνει
δίνει  . Όμως
. Όμως  τυχαίο θετικό, οπότε συμπεραίνουμε ότι για άπειρο πλήθος από
τυχαίο θετικό, οπότε συμπεραίνουμε ότι για άπειρο πλήθος από 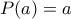 . Αφού
. Αφού  πολυώνυμο, έπεται
πολυώνυμο, έπεται  που χρησιμοποιήσατε; Σίγουρα ο τρόπος σκέψης σας είναι χρήσιμος
που χρησιμοποιήσατε; Σίγουρα ο τρόπος σκέψης σας είναι χρήσιμος
 διότι
διότι 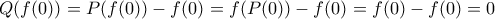
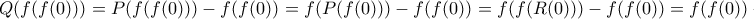
 kok
kok είναι όλοι ρίζες του Q το οποίο ετσι είναι το μηδενικό πολυώνυμο άρα
είναι όλοι ρίζες του Q το οποίο ετσι είναι το μηδενικό πολυώνυμο άρα 